In der Klimadiskussion wird das Argument der Rückkopplung durch Wasserdampf dazu herangezogen, um die Klimawirkung der Treibhausgase — die Sensitivität bei Verdoppelung von deren Konzentration in der Atmosphäre — , die nach Strahlungstransportgleichung und generellem Konsens maximal 0,8° beträgt, um einen angeblichen Faktor 2-6 zu verstärken. Allerdings wird das gewöhnlich nicht genauer quantifiziert, es werden in der Regel nur Formeln mit dem „finalen Feedback“ angegeben.
Vor kurzem haben David Coe, Walter Fabinski und Gerhard Wiegleb in der Publikation „The Impact of CO2, H2O and Other ‚Greenhouse Gases‘ on Equilibrium Earth Temperatures“ unter anderem genau diese Rückkopplung beschrieben und analysiert. In Anlehnung an ihre Publikation wird dieser Effekt mit dem teils gleichen, teils leicht unterschiedlichen Ansatz im folgenden hergeleitet. Die Ergebnisse sind fast identisch.
Dabei wird hier von allen anderen Effekten, die bei der Bildung von Wasserdampf auftreten, wie z.B. Wolkenbildung, abgesehen.
Der grundsätzliche Mechanismus der Wasserdampfrückkopplung
Ausgangspunkt ist eine Temperaturerhöhung der Atmosphäre um ∆T0, ungeachtet deren Ursache. Typischerweise wird der Treibhauseffekt als primäre Ursache angenommen. Die Argumentation ist nun, dass die erwärmte Atmosphäre mehr Wasserdampf aufnehmen kann, d.h. der Sättigungsdampfdruck (SVP = „Saturation Water Pressure“) erhöht sich und es wird angenommen, dass sich konsequenterweise auch die Wasserdampfkonzentration ∆H2O erhöht, und zwar als lineare Funktion der Temperaturänderung. (Die Temperaturänderung ist so klein, dass eine Linearisierung auf jeden Fall legitim ist): ![]()
Dabei ist ![]() die Proportionalitätskonstante für die Wasserdampfkonzentration.
die Proportionalitätskonstante für die Wasserdampfkonzentration.
Eine erhöhte Wasserdampfkonzentration bewirkt wiederum aufgrund der Treibhauswirkung von Wasserdampf eine Temperaturerhöhung, die linear von der Wasserdampfkonzentration abhängt: ![]()
Zusammengefaßt bewirkt also die auslösende Temperaturerhöhung ∆T0 eine Folgeerhöhung der Temperatur ∆T1:![]()
Da die Voraussetzung des Verfahrens ist, dass die Ursache der auslösenden Temperaturerhöhung unerheblich ist, bewirkt die Erhöhung um ∆T1 natürlich ebenfalls wieder einen Rückkopplungszyklus:![]()
Dies wiederholt sich rekursiv. Die finale Temperaturänderung ist demnach eine geometrische Reihe:![]()
Wäre ![]() , würde die Reihe divergieren und die Temperatur über alle Grenzen wachsen. Daher ist es wichtig, sich über die Größe dieser beiden Rückkopplungsfaktoren Klarheit zu verschaffen.
, würde die Reihe divergieren und die Temperatur über alle Grenzen wachsen. Daher ist es wichtig, sich über die Größe dieser beiden Rückkopplungsfaktoren Klarheit zu verschaffen.
Abhängigkeit der möglichen Wasserdampfkonzentration von der Temperatur
Die maximal mögliche Wasserdampfkonzentratio in Abhängigkeit von der Temperatur T (in °C) ist durch den Sättigungsdampfdruck SVP (englisch „saturation vapour pressure“, SVP) begrenzt. Dieser wird durch die Arden Buck Gleichung, (eine moderne, überarbeitete Version der Magnus-Formel) sehr genau beschrieben:![]()
Es wird hier die Standard-Atmosphäre mit 15°C Boden- bzw. Wasseroberflächentemperatur und adiabatischem Temperaturgradient von -6.5°C/km betrachtet.
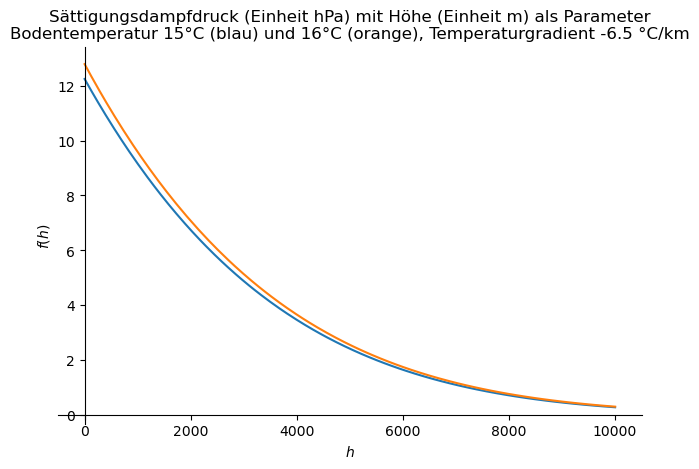
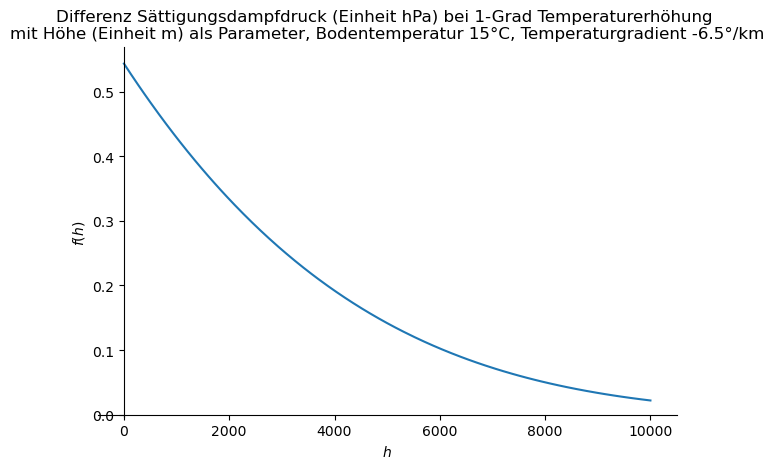
Die absolute Differenz ![]() ist naturgemäß bei höheren Temperaturen, also in Bodennähe, am größten:
ist naturgemäß bei höheren Temperaturen, also in Bodennähe, am größten:
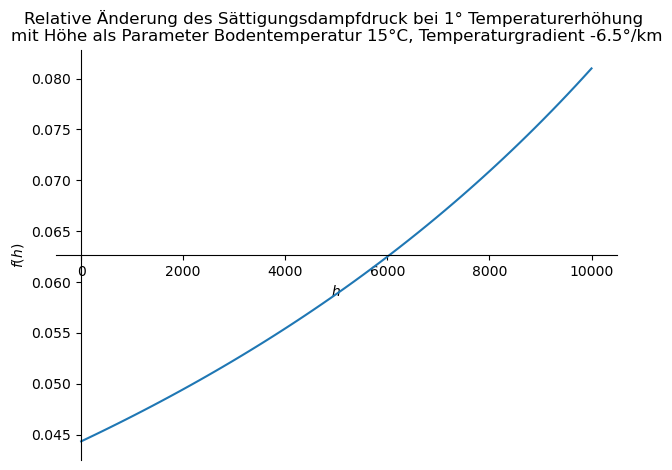
Die relative Differenz ![]() wird mit zunehmender Höhe größer, bewegt sich zwischen 4% und 8%.
wird mit zunehmender Höhe größer, bewegt sich zwischen 4% und 8%.
Die mögliche Zunahme der relativen Luftfeuchtigkeit – das Verhältnis des tatsächlichen Dampfdrucks im Vergleich zum Sättigungsdampfdrucks – als Folge der globalen Temperaturerhöhung ![]() ist durch diese relative Änderung des Sättigungsdampfdrucks begrenzt.
ist durch diese relative Änderung des Sättigungsdampfdrucks begrenzt.
Da die mittlere, dominante Infrarot-Abstrahlung der Erde etwa in der Höhe 5000m stattfindet, und sich oberhalb davon kaum mehr Wasserdampf befindet, ist es sinnvoll, 6% als oberes Limit der Änderung der relativen Luftfeuchtigkeit infolge einer Temperaturerhöhung um 1°C anzunehmen. Demzufolge ergibt sich die Konstante ![]() als
als ![]() . Dieser Wert ist etwas kleiner als die üblicherweise genannten (aber gewöhnlich nicht belegten) 7%. Nach dem obigen Diagramm wären 7% Erhöhung des Wasserdampfgehalts erst oberhalb von 8000 m ü.d.M. möglich.
. Dieser Wert ist etwas kleiner als die üblicherweise genannten (aber gewöhnlich nicht belegten) 7%. Nach dem obigen Diagramm wären 7% Erhöhung des Wasserdampfgehalts erst oberhalb von 8000 m ü.d.M. möglich.
Die 6% bzw. 7% sind eine maximale Obergrenze der Wasserdampfaufnahme bei Temperaturerhöhung um 1°C. Das muss aber nicht heißen, dass das tatsächlich auch geschieht. Nach Tabelle 3 der Publikation „Global Changes in Water Vapor 1979–2020“ beträgt während der untersuchten 4 Jahrzehnte die aus Klimamodellen berechnete Sensitivität der Änderung des Wasserdampfes von der Temperatur etwa 5% pro °C Erwärmung.
Abhängigkeit des Treibhauseffekts von Änderungen des Wasserdampfgehalt
Der Infrarot Strahlungstransport in der Atmosphäre ist vom Wasserdampfgehalt abhängig. Dies wird in dem bekannten und bewährten Simulationsprogram MODTRAN berücksichtigt. Mit zunehmendem Wasserdampfgehalt sinkt infolge des Treibhauseffektes des Wasserdampfes die ausgehende Infrarotstrahlung.
Die in MODTRAN verwendete US-Standardatmosphäre hat als Default-Voreinstellung 15mm für den niederschlagsfähigen Wasserdampf. Der weltweite durchschnittliche niederschlagsfähige Wasserdampf ist 25mm, was etwa einem Wasserdampffaktor 1.7 bei MODTRAN entspricht.
Zur Vereinfachung und um eine obere Grenze für die Rückkopplung zu erhalten, betrachten wir hier nur den wolkenlosen Fall („clear sky“).
Dazu stellen wir die Parameter der MODTRAN Simulation auf
- die aktuelle CO2-Konzentration von 420 ppm,
- die Wasserdampfskala auf 1.7 (entspricht 25mm niederschlagsfähiger Wasserdampf)
- Der Zustand wird gespeichert
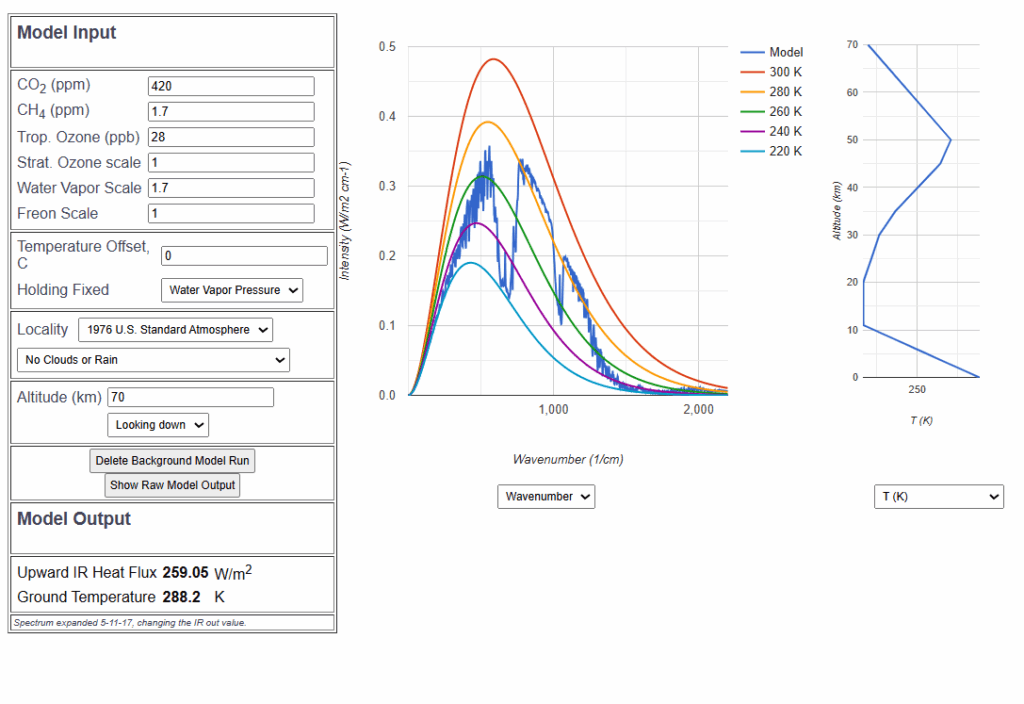
Dann wird der Wasserdampffaktor um 5% auf 1.785 verändert. Das bewirkt eine Verringerung der IR Abstrahlung um 0.88 ![]() .
.
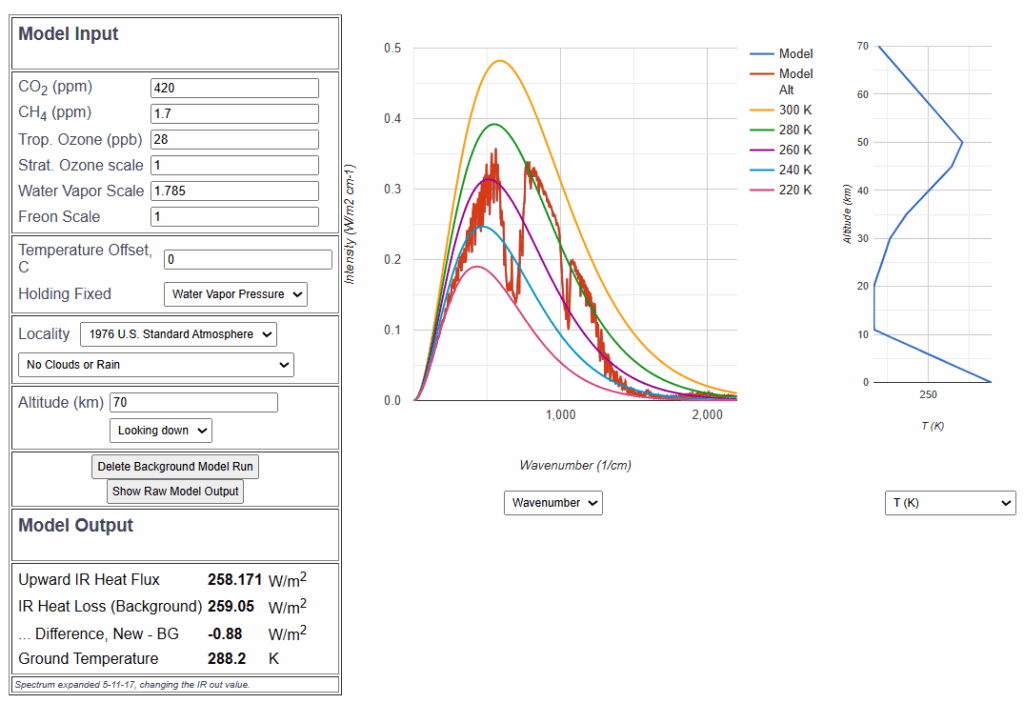
Dann wird der Temperatur-Offset so lange vergrößert, bis die reduzierte IR-Abstrahlung von 0.88 ![]() durch Temperaturerhöhung wieder ausgeglichen ist. Dies ist bei einer Erhöhung der Bodentemperatur um 0.22 °C der Fall.
durch Temperaturerhöhung wieder ausgeglichen ist. Dies ist bei einer Erhöhung der Bodentemperatur um 0.22 °C der Fall.
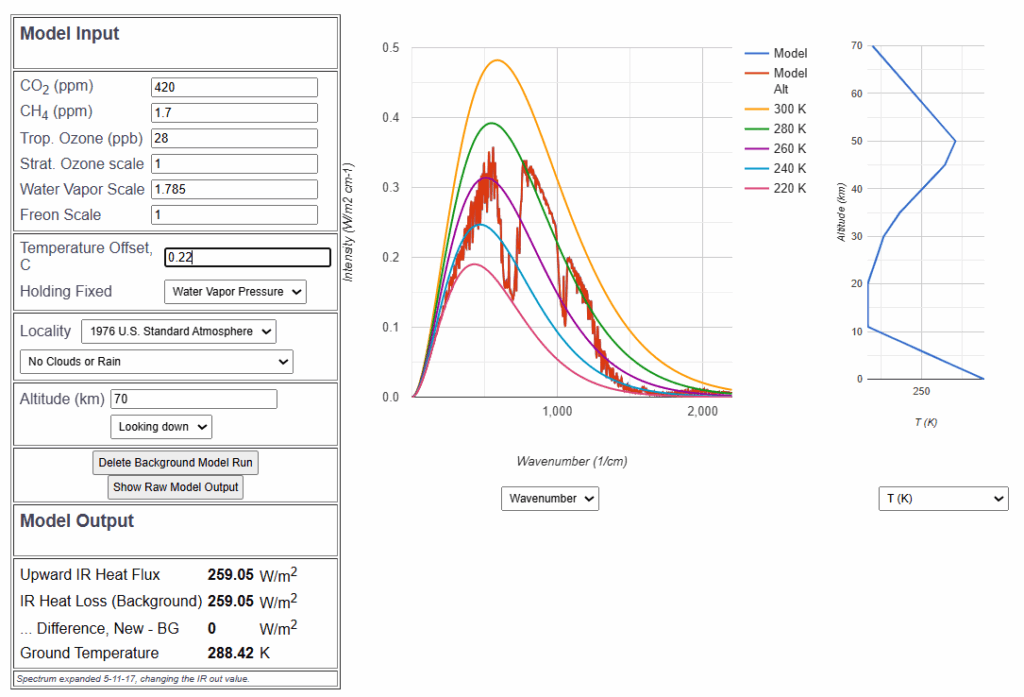
Eine 5% höherer Wasserdampfgehalt infolge einer Temperaturerhöhung um 1°C bewirkt also einen Treibhauseffekt, der durch eine Temperaturerhöhung von 0.22°C ausgeglichen wird.
Der finale Rückkopplungsfaktor und der gesamte Treibhauseffekt
Die geometrische Reihe führt zu einem Verstärkungsfaktor ![]() des reinen CO
des reinen CO![]() Treibhauseffekts um
Treibhauseffekts um ![]()
Damit ist die um die Wasserdampfrückkopplung verstärkte „clear sky“ Sensitivität bei Verdopplung der CO![]() Konzentration
Konzentration ![]() nicht mehr
nicht mehr ![]() °C, sondern
°C, sondern ![]() °C = 1°C
°C = 1°C
Eine differenzierte Betrachtung der wolkenlosen Gebiete (33%) mit einem niederschlagsfähigen Wasserdampfgehalt von 21mm und den wolkigen Gebieten (67%) mit einem niederschlagsfähigen Wasserdampfgehalt von 28mm führt zu einem deutlich niedrigeren Rückkopplungsfaktor von etwa 1.16.

Danke, sehr schön erklärt. Für CO2 ist das auch vollständig, mit der erwähnten Unsicherheit infolge Wolkenbildung. In den Modellen scheint die Wasserdampferhöhung größer zu sein. Woher kommt das (wir haben noch nicht einmal eine Verdopplung von CO2 erreicht)? Ferner findet eine Wasserdampferhöhung bei jeder T-Erhöhung unabhängig von der Ursache statt, d.h. also auch z.B. bei einer Veränderung der Sonneneinstrahlung. Wird das in den Modellen berücksichtigt (unabhängig von der Tatsache, dass die Modelle u.U. mit falschen, historisch normierten Sonneneinstrahlungswerten laufen (siehe z.B. SOON et al). Nach meiner Erinnerung hat Prof. Harde die insgesamt zu berücksichtigende Wasserdampfverstärkung den verschiedenen Temperaturtreibern in einer Veröffentlichung zugeordnet und kommt dann auf eine wesentlich kleineren Wert, der dem CO2 zugeschrieben werden kann als dies in den Modellen berechnet wird. Aber klar, das sind dann die Rückkopplungen des Gesamtsystems, inklusive Wolkenbildung, unter Berücksichtigung aller T-Treiber, wenn ich es richtig verstanden habe. Haben Sie auch das Gesamtsystem kommentiert?