Anteile der anthropogenen und der natürlichen Emissionen am Anstieg der CO2-Konzentration

Aus der Publikation Improvements and Extension of the Linear Carbon Sink Model geht hervor, dass die globale natürliche effektive Senkenwirkung sowohl von der CO2-Konzentration als auch von der globalen (Meeresoberflächen-)Temperaturanomalie abhängen. Dazu hier eine kurze Herleitung der Zusammenhänge. Im Gegensatz zur zitierten Publikation wird hier mit monatlichen anthropogenen Emissionsdaten und monatlichen Konzentrationsdaten Daten mit fortlaufenden Monaten gerechnet.

Die Massenerhaltung bzw. die Kontinuitätsgleichung bedeutet, dass sich das monatliche Konzentrationswachstum

zwingend aus der Summe der anthropogenen Emissionen und der natürlichen Emissionen , vermindert um die monatlichen Absorptionen ergibt:

(1)  

Die effektive Senkenwirkung ist die Differenz zwischen anthropogenen Emissionen und dem Konzentrationswachstum:

(2)  

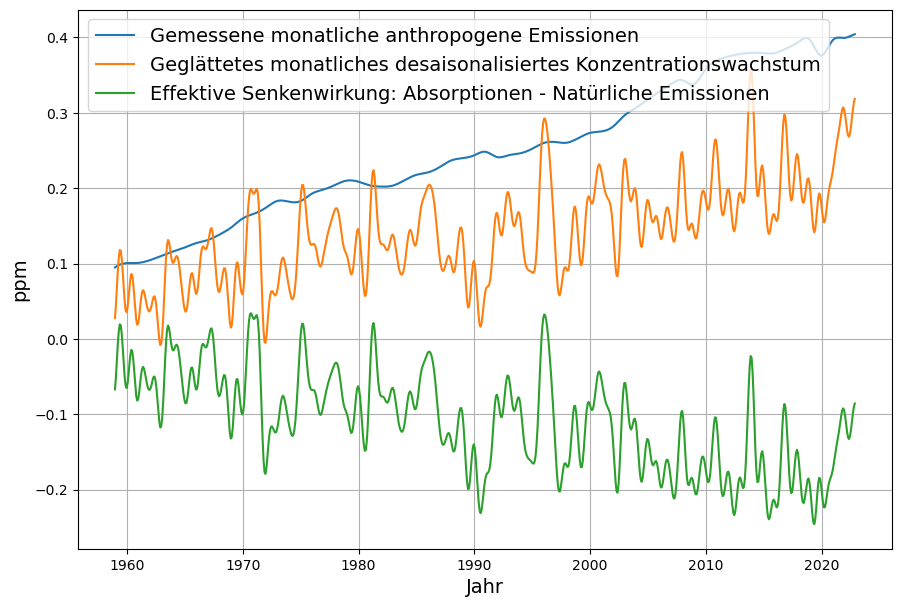
Aus Gleichung 1 folgt unmittelbar, dass die effektive, also direkt messbare Senkenwirkung nicht nur Absorptionen durch die Ozeane und Pflanzen, sondern implizit auch sämtliche natürliche Emissionen enthält:

Daher ist die Senkenwirkung nicht identisch mit der Summe sämtlicher Absorptionen, sondern nur den Anteil der Absorptionen, die nicht durch natürliche Emissionen kompensiert wurden.

Aus der Arbeit „Improvements and Extension of the Linear Carbon Sink Model“ ergibt sich, dass die globale effektive Senkenwirkung durch ein erweitertes Modell aus CO Konzentration und globaler Meeresoberflächentemperatur gut beschrieben wird:

(3)  

Zum Vergleich wird das in der Arbeit „Emissions and CO₂ Concentration—An Evidence Based Approach“ beschriebene einfache Senkenmodell verwendet, das nur von der CO Konzentration abhängt:

(4)  

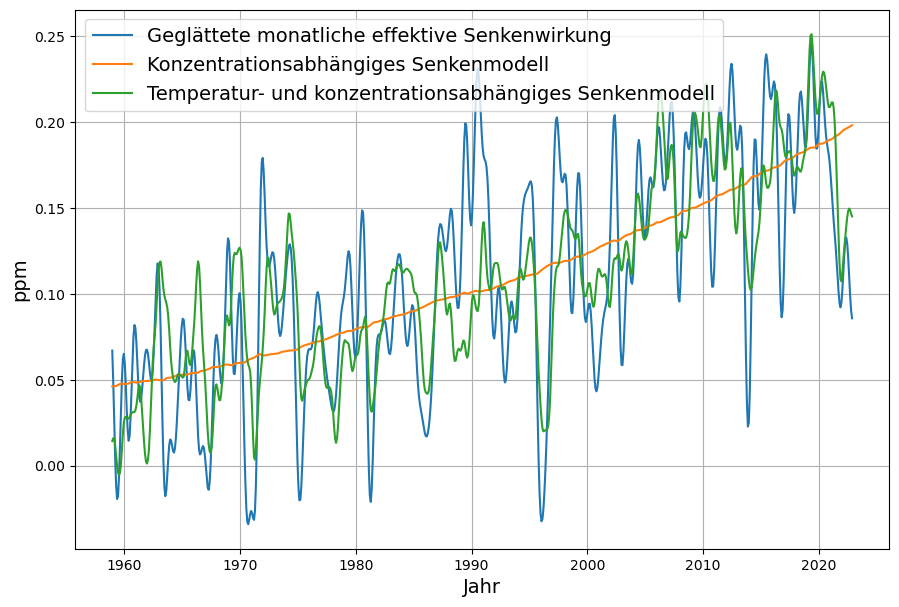
Die Abbildung 2 zeigt, dass das einfache Modell den Trend sehr gut wiedergibt, dass aber die Schwankungen erst durch das erweiterte Modell, also durch Einbeziehen der Meeresoberflächentemperatur beschrieben werden können. Die Parameter für die beste Anpassung des erweiterten Modells sind , ppm/°C, ppm.

Mit den Gleichungen 2 und 3 bzw. 4 lässt sich auch der Konzentrationsanstieg modellieren:

(5)  

Dies wird in Abb. 3 gezeigt. Zum Vergleich auch hier wieder die Rekonstruktion mit dem einfachen Senkenmodell.

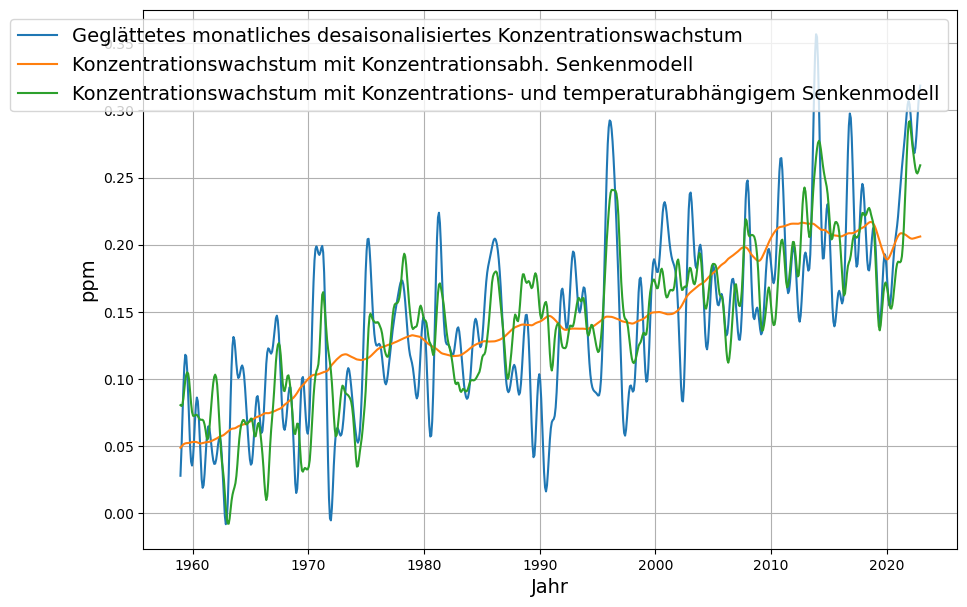
Rekonstruktion der Konzentration, Unterscheidung des Einflusses von Emissionen und Temperatur

Aus dem Konzentrationswachstum lässt sich mit Hilfe der initialen CO Konzentration , hier also der Konzentration im Dezember 1958, der Verlauf der CO Konzentration rekonstruieren.
Nach Gleichung 5 wird das Konzentrationswachstum von den äußeren Zustandsgrößen der anthropogenen Emissionen und der Temperatur gesteuert. Zusammen mit dem ermittelten Parameter ergibt der Term die Veränderung der natürlichen Emissionen aufgrund der Temperaturanomalie .
Daher ist es zunächst interessant, die Größenordnungen beider Emissionsquellen miteinander zu vergleichen. Als Maßeinheit der Emissionen wird GtC verwendet, die sich durch Multiplikation der sonst in ppm gemessenen Größen mit 2,123 ergibt.

Abb. 4 zeigt die anthropogenen Emissionen seit 1959 und die natürlichen Emissionen aufgrund der Temperaturskala der Anomalie der Meeresoberflächentemperaturen. Es fällt auf, dass vor 1975 die Temperaturen und damit die natürlichen Emissionen überwiegend negativ sind. Das hängt mit der willkürlichen Wahl des Nullpunkts der Anomalie-Temperaturskala zusammen.

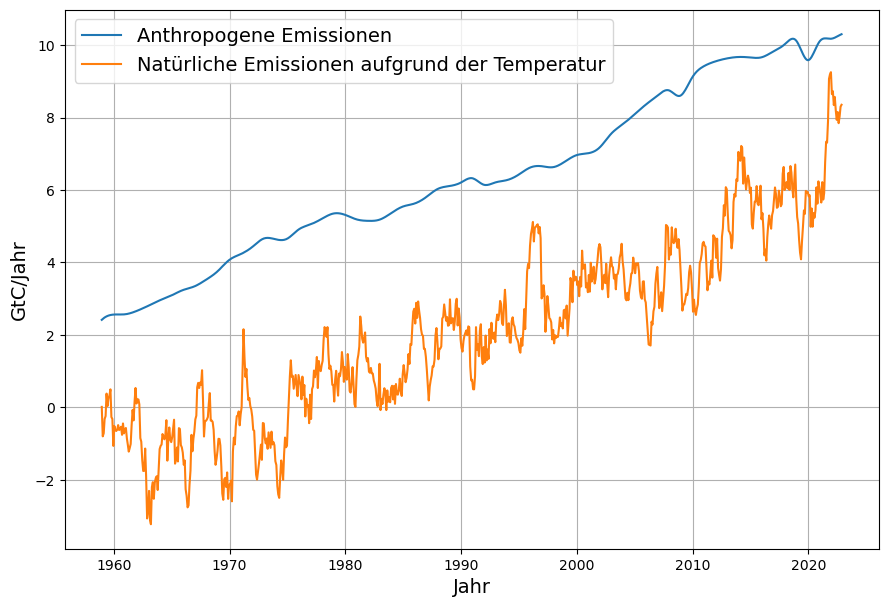
Weiter fällt auf, dass die anthropogenen Emissionen im Schnitt etwa 4 GtC größer sind als die natürlichen. Insgesamt sind die natürlichen Emissionen zahlenmäßig noch sehr viel größer, da der konstante Term von etwa 34 GtC (16\cdot 2,123) auch natürliche Emissionen darstellt. Diese konstanten natürlichen Emissionen definieren laut Gleichung 14 in Improvements and Extension of the Linear Carbon Sink Model die Gleichgewichtskonzentration bei der Temperaturanomalie 0°, mit den aktuellen Zahlen ist diese Gleichgewichtskonzentration 307 ppm. Das ist nicht der vorindustrielle Zustand, dieser hat die Temperaturanomalie -0,48°.

In Abb. 5 sind 3 ausgewählte Modellszenarien dargestellt. Außer den tatsächlich gemessenen Konzentrationswerten zunächst die Rekonstruktion mit dem tatsächlichen Temperatur- und Emissionsverlauf (orange). Diese bleibt erwartungsgemäß sehr nahe an den Messdaten.

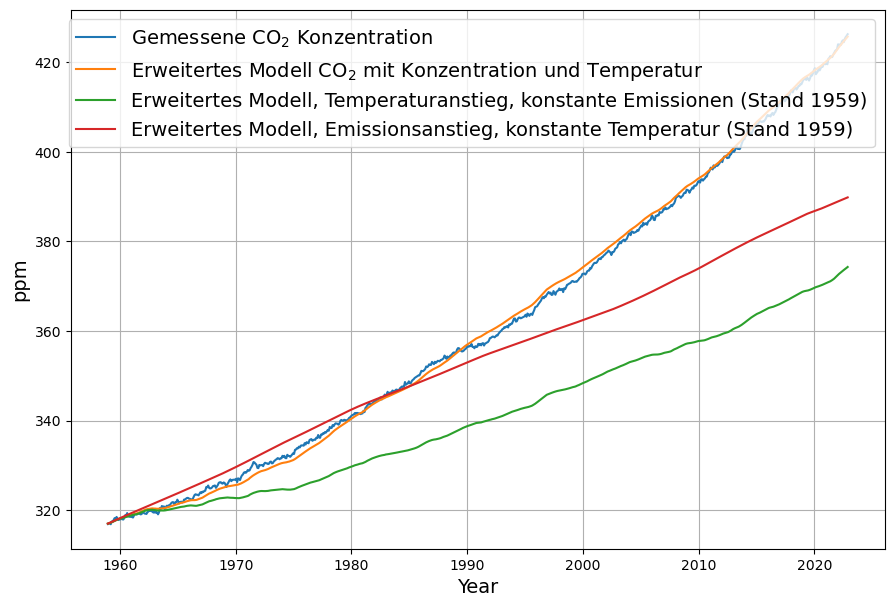
Zusätzlich werden 2 weitere Szenarien dargestellt:

• Die anthropogenen Emissionen bleiben auf dem Stand von 1959 und nur die Temperatur entwickelt sich so weiter wie wir es kennen (grüne Farbe). Die CO Konzentration wächst bis etwa 370 ppm an.
• Die Temperatur bleibt auf dem Stand von 1959, die anthropogenen Emissionen wachsen aber wie gewohnt. Die Konzentration steigt zunächst steiler and als wenn die Temperatur sich auch verändern würde. Das kommt daher, dass die Temperaturanomalie bis Mitte der 70er Jahre unter 0 bleibt. Erst nach 1983 bleibt die resultierende Konzentration unter dem Referenzwert. Insgesamt haben die anthropogenen Emissionen einen größeren Anteil am Konzentrationswachstum als die natürlichen, aber 2023 z.B. kommen der natürliche dem anthropogenen Emissionsanteil sehr nahe.

Es fällt auch auf, dass die Auswirkungen beider Emissionsquellen in Form von resultierender Konzentration sich nicht einfach addieren lassen. Die Konzentration aus der Summe ist geringer als die Summe der Konzentrationen beiden Emissionsanteile. Das hat damit zu tun, dass mit wachsender Konzentration die Absorptionen zunehmen. Beide Emissionsquellen haben zusammen einen kleineren Effekt auf die Konzentration als man vom jeweiligen Einzeleffekt intuitiv erwarten würde.

Fazit

Das erweiterte Senkenmodell erlaubt es, die Auswirkungen von anthropogenen Emissionen und Temperaturerhöhungen auf die CO Konzentration separat zu betrachten. Das Ergebnis widerspricht denjenigen, die der Auffassung sind, dass die anthropogenen Emissionen vollständig die Konzentrationsänderungen seit dem Beginn der Industrialisierung erklären. Aber es widerspricht auch denjenigen, die behaupten, aufgrund des großen Umsatzes des natürlichen Kohlenstoffkreislaufs spielten die anthropogenen Emissionen gar keine Rolle. Die Wahrheit ist, dass beide Faktoren einen größenordnungsmäßig ähnlichen Einfluss haben, die anthropogenen Emissionen allerdings etwas überwiegen.