CO₂ Sensitivität mit Wasserdampf und Wolken

Der häufig verwendete, auf die Untersuchungen von Myhre zurückgehende Wert der CO₂-Sensitivität beträgt etwa . Dieser beruht allerdings auf der Bedingung, dass der Himmel wolkenlos und ohne Wasserdampf ist, was eine Abstrahlung von impliziert, eine für einen globalen Mittelwert völlig unrealistische Annahme. Hier die zugehörige Simulation mit MODTRAN:

Um eine im globalen Mittel realistische Sensitivität zu erreichen, muss mit der tatsächlichen Abstrahlung von gerechnet werden, mit der das globale Strahlungsgleichgewicht erreicht wird.

Um das zu simulieren, müssen sowohl Wolken als auch Wasserdampf berücksichtigt werden.
Hierzu werden folgende, aus Literaturrecherche ermittelte folgende Annahmen getroffen:

• Der Anteil der von Wolken bedeckten Erdoberfläche ist etwa 67%,
• Der global durchschnittliche niederschlagsfähige Wasserdampf (PWV) ist bei Wolkendecke 28 mm und bei wolkenlosem Himmel 21 mm. Im Simulationsprogramm MODTRAN ist der angenommene Defaultwert des Wasserdampfes bei der US Standardatmosphäre etwa 15 mm (dem durchschnittlichen Wert der USA), demzufolge ergibt sich bei Wolken für den „Water Vapor Scale“ Parameter 1.87 und bei wolkenlosem Himmel 1.4.
• Als Wolkenart wird vereinfachend die häufigste Wolkenart der Kumuluswolken gewählt. Die Einbeziehung weiterer Wolkenarten können das Ergebnis noch geringfügig verändern.

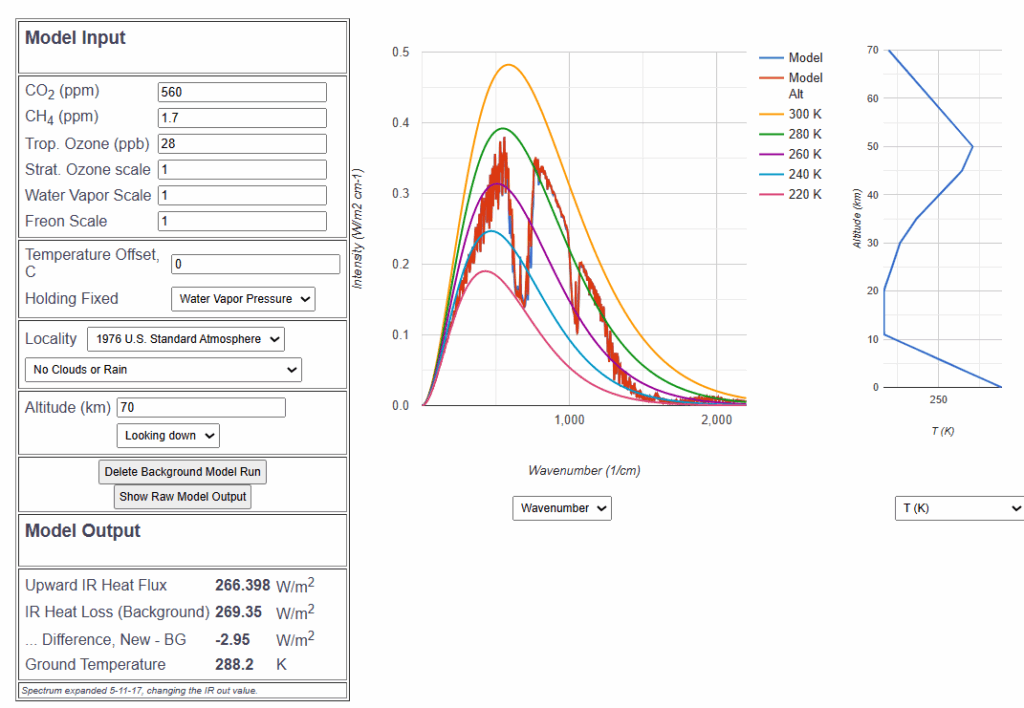
Simulation wolkenloser Himmel

Die Defaultsimulation von MODTRAN wird modifiziert:

• CO2-Konzentration 280 ppm
• Water Vapor Scale: 1.4
• Locality: US Standard Atmosphere 1976

Als IR-Fluss ergeben sich . Dieser Zustand wird gespeichert. Danach wird die CO₂-Konzentration auf 560 ppm verdoppelt:

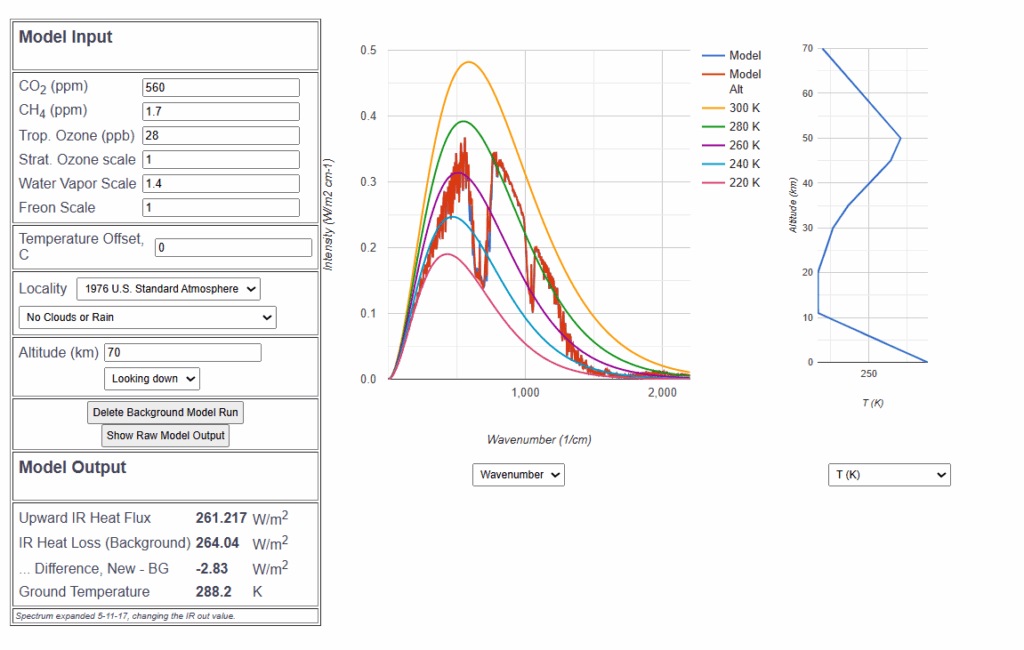
Der Strahlungsantrieb aufgrund der CO₂-Verdoppelung ist also , was trotz der „clear sky“ Annahme bereits deutlich weniger ist als der beim IPCC üblicherweise verwendete Wert von über . Doch es fehlt noch die Berücksichtigung des Anteils der von Wolken bedeckten Erdoberfläche.

Simulation des von Wolken bedeckten Teils der Atmosphäre

Die Defaultsimulation von MODTRAN wird modifiziert:

• CO₂-Konzentration 280 ppm
• Water Vapor Scale: 1.87
• Locality: US Standard Atmosphere 1976
• Als Wolkenbedeckung wird die „Cumulus Cloud Base“ gewählt.

Als IR-Fluss ergeben sich . Dieser Zustand wird gespeichert. Danach wird die CO₂-Konzentration auf 560 ppm verdoppelt:

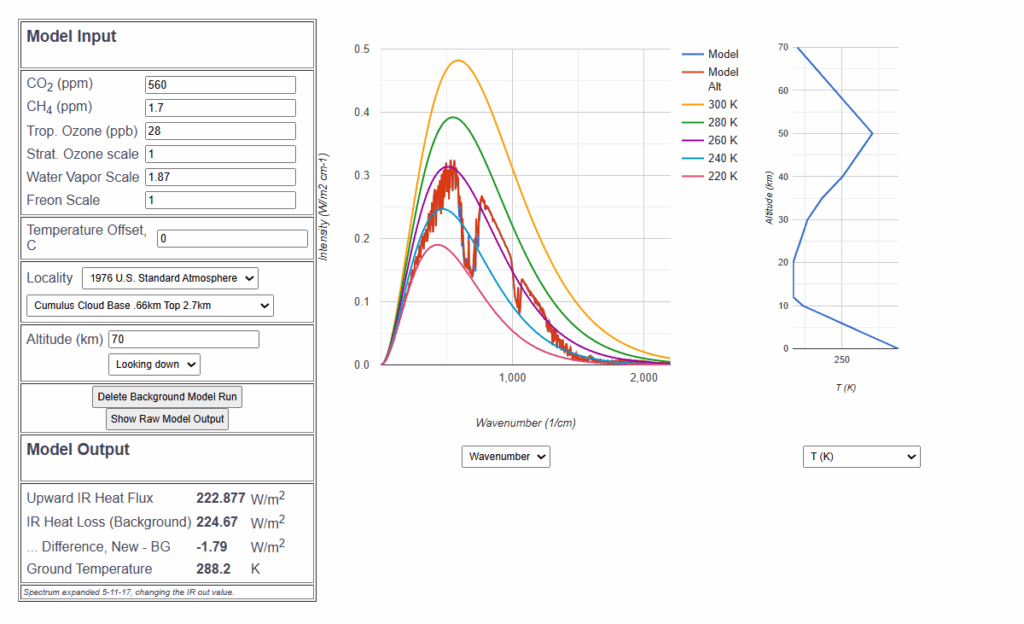
Der Strahlungsantrieb aufgrund der CO₂-Verdoppelung ist unter diesen Bedingungen . Mit der Wahl des Wolkenmodells „Altostratus“ wäre dieser Strahlungsantrieb , der maximale Wert ergibt sich beim „Nimbostratus“ Modell mit .

Validierung des Strahlungsgleichgewichts und Bestimmung der CO₂-Sensitivität

Um das globale Gleichgewicht zwischen Einstrahlung () und Abstrahlung zu überprüfen, wird die mit dem Grad der Wolkenbedeckung gewichtete Summe der IR Flüsse der beiden Modelle gebildet:

Angesichts der möglichen Variabilität der Ausgangsparameter kann dieser Wert als „Punktlandung“ betrachtet werden.
Bei Verwendung anderer Wolkenmodelle muss darauf geachtet werden, dass dieses Strahlungsgleichgewicht eingehalten wird.

Der Gesamtstrahlungsantrieb ist die gewichtete Summe der Antriebe aus dem Wolkenmodell und dem wolkenlosen Modell:

Die CO₂-Sensitivität wird mit der Ableitung der Stefan-Boltzmann-Gleichung aus dem IR Fluss und dem Strahlungsantrieb berechnet:

Demnach reduzieren sowohl Wolken als auch zunehmender Wasserdampfgehalt die CO₂-Sensitvität signifikant. Beides muß für eine realistische Berechnung des Treibhauseffekts berücksichtigt werden.