Der Wendepunkt der CO2-Konzentration

Und steigt und steigt…?

Auf den ersten Blick steigt die atmosphärische CO₂-Konzentration fortwährend an, dargestellt an den Jahresmittelwerten, die in Maona Loa gemessen werden (ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_mm_mlo.txt):

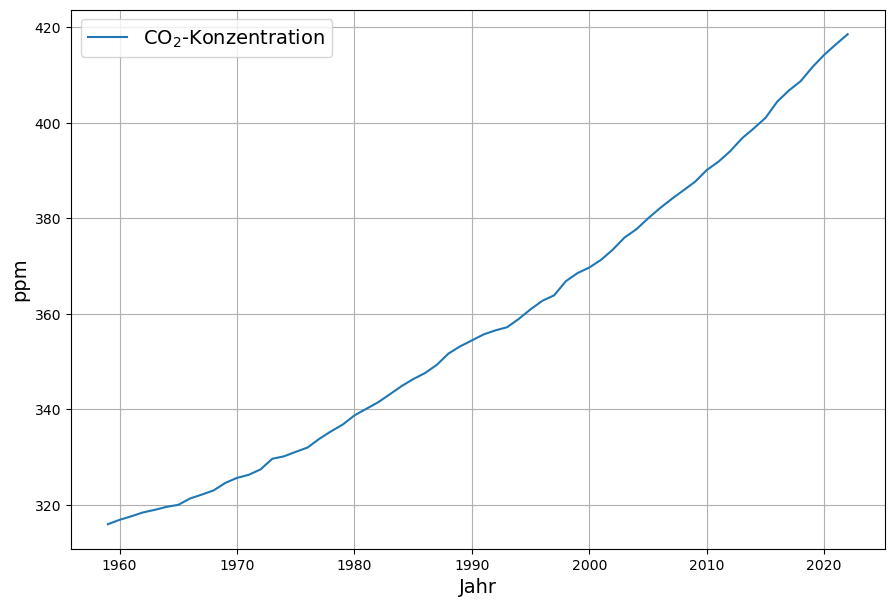
Die zentrale Frage, die sich stellt, ist die, ob die Konzentration immer schneller wächst, d.h. ob jedes Jahr mehr dazukommt? Dann wäre die Kurve konkav, also also nach oben gekrümmt.

Oder wird der jährliche Anstieg der Konzentration immer geringer? Dann wäre sie konvex, also nach unten gekrümmt.

Oder gibt es einen Übergang, also einen Wendepunkt im mathematischen Sinne? Das wäre daran zu erkennen, dass zunächst der jährliche Zuwachs immer größer wird, und ab einem bestimmten Zeitpunkt abnimmt.

Auf den ersten Blick erscheint die Gesamtkurve konkav, was bedeutet dass der jährliche Anstieg der Konzentration mit jedem Jahr augenscheinlich zunimmt.

Die Beantwortung dieser Frage ist entscheidend für die Frage, wie dringend Maßnahmen zur Eindämmung von CO2 Emissionen sind.

Genauere Untersuchung mit dem gemessenen jährlichen Anstieg

Um einen genaueren Eindruck zu bekommen, berechnen wir den jährlichen Anstieg der CO2-Konzentration (Stand 2023):

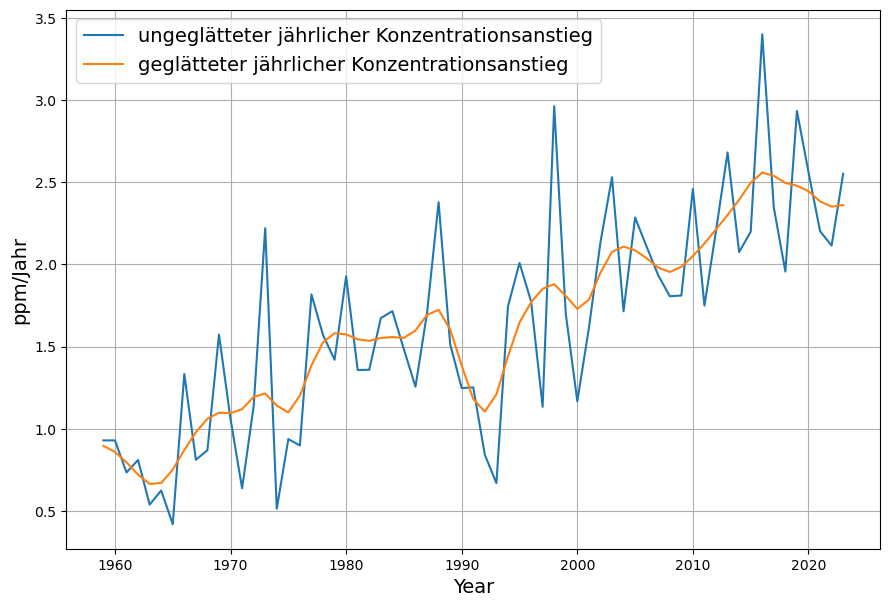
Damit bestätigt sich, dass bis 2016 ein klarer Trend zu immer höherem jährlichen Konzentrationsanstieg bestand, von knapp 0.75 ppm/Jahr im Jahre 1960 bis über 2.5 ppm/Jahr im Jahre 2016.

Seit 2016 geht jedoch der jährliche Anstieg zurück. Dabei spielt gewiss der Corona-bedingte Emissionsrückgang eine Rolle, dieser erklärt aber nicht den bereits 2016 einsetzenden Rückgang.

Es gibt also in der Konzentrationskurve im Jahre 2016 einen Wendepunkt, eine Trendumkehr von zunehmendem Konzentrationswachstum zu abnehmendem Konzentrationswachstum. Gibt es dafür eine zufriedenstellende Erklärung? Dies ist wesentlich, denn wenn wir absehen können, dass der Trend zurückgehenden Anwachsens der Konzentration anhält, dann ist absehbar, dass die Konzentration irgendwann nicht mehr weiter ansteigt und das Ziel des Pariser Klimaabkommens, das Gleichgewicht zwischen CO₂-Quellen und CO₂-Senken erreicht werden kann.

Erklärung durch stagnierende Emissionen

Im Rahmen des Global Carbon Brief Projekts hat Zeke Hausfather 2021 aufgrund neuer Erkenntnisse die Werte der globalen CO₂-Emissionen der letzten 20 Jahre revidiert, mit dem wichtigen Ergebnis, dass die globalen Emissionen seit 10 Jahre im Rahmen der Messgenauigkeit konstant sind:

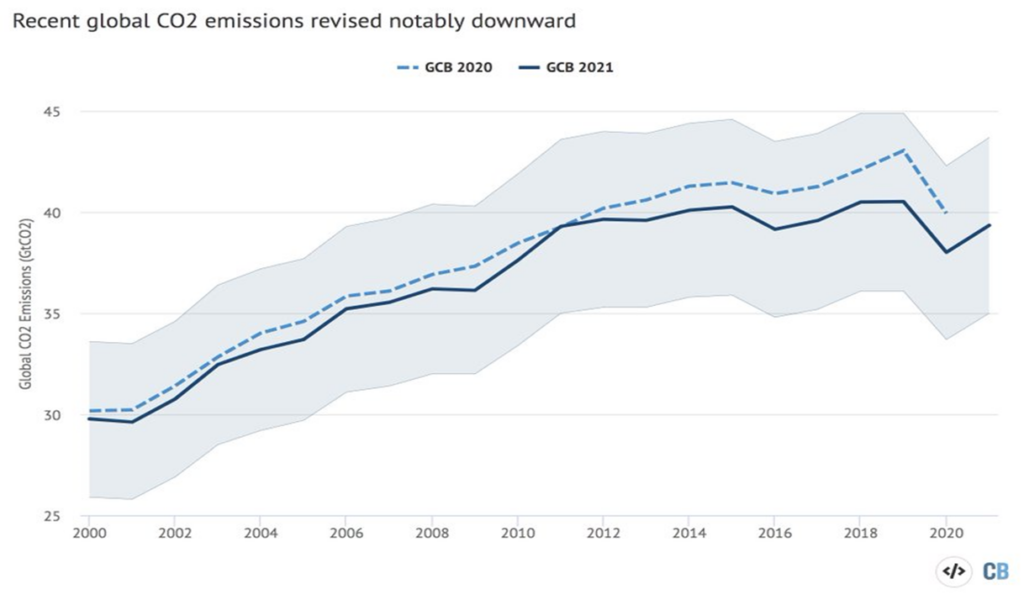
Um die Auswirkungen dieser wichtigen Erkenntnis zu bewerten, muss man den Zusammenhang zwischen Emissionen und CO₂-Konzentration kennen.

Aus meinen eigenen Recherchen dazu in einer Publikation und in einem danach mit neuen Erkenntnissen ergänzten Blogbeitrag folgt, dass sich der Konzentrationsanstieg aus den Emissionen und den Absorptionen ergibt, die proportional zur CO₂-Konzentration sind. Dieses Modell wurde in ähnlicher Form auch von anderen beschrieben und publiziert:

• Prof. Vollmer und Prof. Eberhardt A simple model for the prediction of CO₂ concentrations in the atmosphere, depending on global CO₂ emissions
• Prof. Ganteför in einem Videovortrag darüber,
• Prof. Vahrenholt, in der Publikation „Oceans’ surface pH-value as an example of a reversible natural response to an anthropogenic perturbation„,
• Dr. Roy Spencer in der Blog-Publikation „A Simple Model of the Atmospheric CO2 Budget„,
• Ari Halparin in der Blog-Publikation „Simple Equation of Multi-Decadal Atmospheric Carbon Concentration Change„,
• Peter Dietze in seinem Beitrag zum 3. IPCC Zustandsbericht ( IPCC’s Most Essential Model Errors), seinen vorausgegangenen Publikationen, 1995-1998 (verfügbar mit Quellenangaben unter Little Warming with new Global Carbon Cycle Model und Carbon Model Calculations samt Gutachter-Diskussion http://www.john-daly.com/dietze/cmodcalD.htm , http://www.john-daly.com/dietze/cmodcalc.htm), sowie der neueren der Blog-Publikation „DECARBONISATION? The fatal error caused by false Carbon Models“

Trivialerweise folgt aus der Massenerhaltung, dass die Konzentration am Ende des Jahres aus der Konzentration des Vorjahres , den natürlichen Emissionen , den anthropogenen Emissionen und den Absorptionen ergibt:

(1)  

Daraus ergibt sich unmittelbar die aus Emissionen und gemessenem Konzentrationsanstieg berechneten effektive Absorption:

(2)  

Mit der Definition des Konzentrationswachstums

ergibt sich, dass die gesamte Senkenwirkung sich zwingend aus der Differenz der Emissionen und dem Konzentrationswachstum ergibt – ohne dass man wissen muss, wie diese Senkenwirkung im Detail zustande kommt. Dabei hat diese Gesamtsenkenwirkung zwei Komponenten, und zwar die Jahressumme aller Absorptionen, die zu zusammengefaßt werden, und die als zusammengefaßten sog. „natürlichen Emissionen“, das ist die Jahressumme sämtlicher Emissionen außer den anthropogenen, die separat als geführt werden:

(3)  

Unter der Annahme konstanter jährlicher natürlicher Emissionen

und der linearen Modellannahme, also dass die Absorptionen proportional zur Konzentration des Vorjahres sind,

wird das Absorptionsmodell als lineares Modell der Konzentration erstellt (diese beiden Annahmen werden ausführlich in der Publikation begründet):

(4)  

Mit läßt sich die Modellgleichung umformulieren, es ergibt sich damit die Gleichgewichtskonzentration für den Fall von Nullemissionen, also die vorindustrielle Gleichgewichtskonzentration :

(5)  

Die Regressionsrechnung dieses Gleichungssystems mit den aktuellen CO₂ Emissionsdaten (Selektion country = World) liefert das Ergebnis und . Bei dieser Berechnung werden die Emissionen aufgrund von Landnutzungsänderungen nur anteilig (23%) berücksichtigt. Dies erklärt die zahlenmäßigen Unterschiede des Ergebnisses mit denen der zitierten Publikationen. Das geringe Wichtung der Landnutzungsänderungen ist gerechtfertigt:

• Alle Quellen stimmen darin überein, dass die veröffentlichten Werte der Emissionen durch Landnutzungsänderung stark fehlerbehaftet sind,
• Mit der Wichtung der Emissionen durch Landnutzungsänderungen von etwa 25% führt das Modell zu einer Gleichgewichtskonzentration 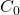, die der vorindustriellen Gleichgewichtskonzentration von etwa 280 ppm entspricht.

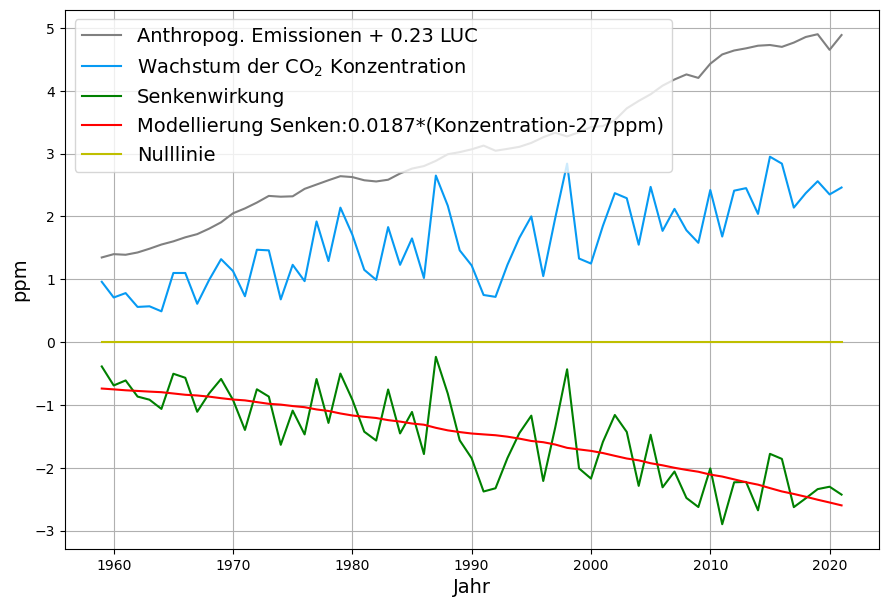
Mit

können aus der modellierten Absorption die variablen jährlichen natürlichen Nettoemissionen ermittelt werden. Deren Mittelwert ist die Konstante .

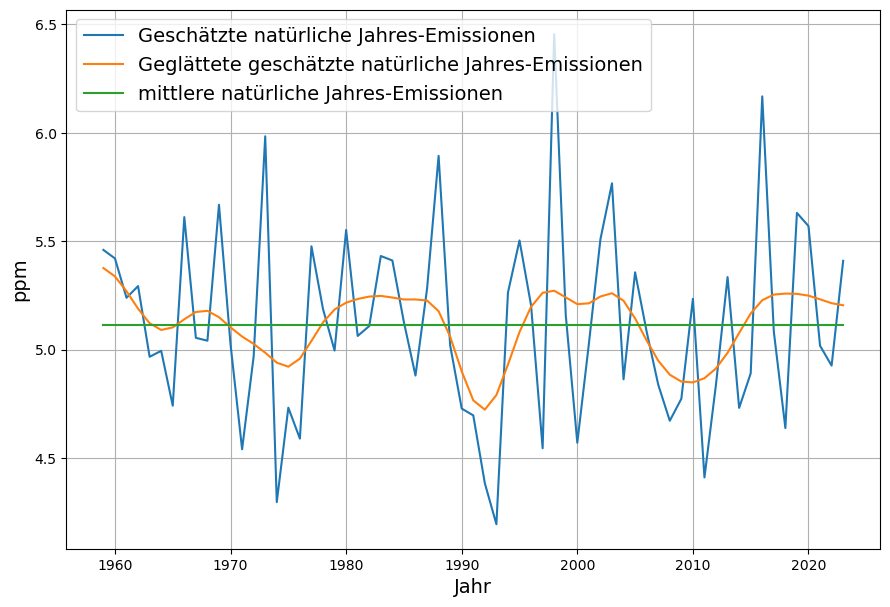
Daraus ist erkennbar, dass die residualen natürlichen Emissionen eine zyklische Komponenten enthalten, die mit dem El Nino und kontingenten Ereignissen wie dem Ausbruch des Pinatubo zusammenhängt.

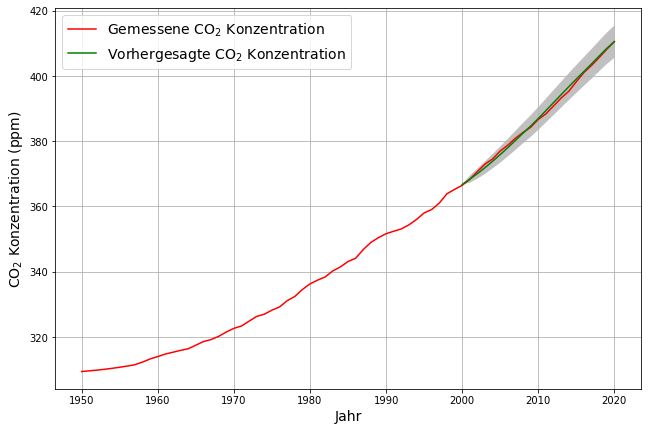
Mit diesem Modell wird die bekannte Konzentration zwischen 2000 und 2020 aus den Daten zwischen 1950-2000 sehr genau prognostiziert. Da das Modell zwar einen linearen Trend, aber keine zyklischen Schwankungen vorsieht – diese landen alle in der Variabilität der natürlichen Emissionen – , zeigt auch die modellierte Konzentration keine zyklischen Schwankungen:

Wachstumsrate der modellierten Konzentration

Die Wachstumsrate der modellierten Konzentration ergibt sich durch Umstellung der Modellgleichung:

Diese zeigt nun auch nicht mehr die zyklischen Schwankungen:

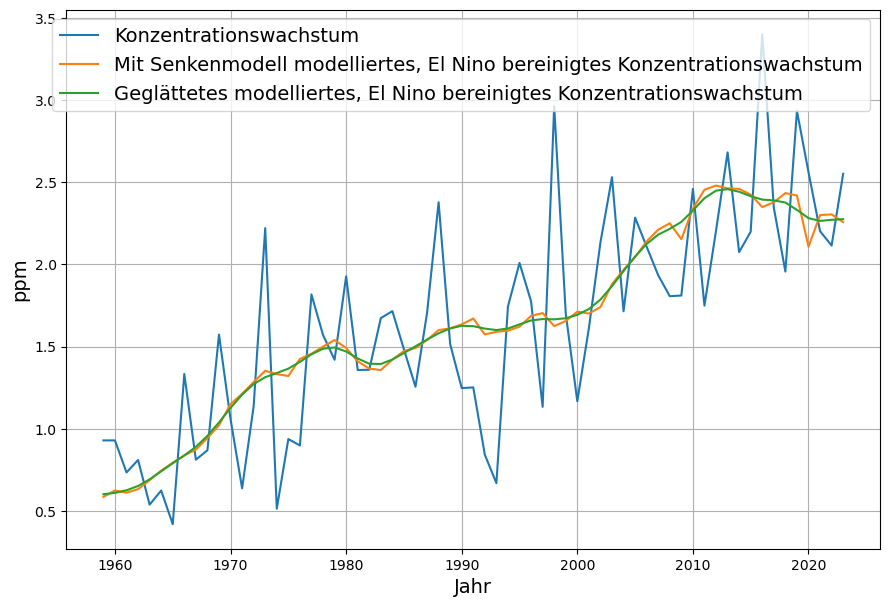
Es bleibt nach wie vor ein globales Maximum, das Jahr des Maximums ist allerdings von 2016 nach 2013 gewandert.
Diese El Nino bereinigte Konzentrationsänderungen bestätigen die Aussage von Zeke Hausfather, dass in der Tat die Emissionen bereits seit 10 Jahre konstant sind.

Entwicklung der CO₂-Konzentration bei konstanten Emissionen

Um den Wendepunkt der CO₂-Konzentration zu verstehen, wollen wir mit der Annahme konstanter Emissionen und den Gleichungen (3) und (5) den prognostizierten Verlauf berechnen:

(6)  

Die linke Seite beschreibt den Anstieg der Konzentration. Auf der rechten Seite wird von den konstanten Emissionen ein mit wachsender Konzentration wachsender Betrag abgezogen, demnach nimmt der Konzentrationszuwachs mit wachsender Konzentration ab. Dies kann mit einem speziellen Bankkonto veranschaulicht werden. Sobald die Konzentration den Wert erreicht, ist der Gleichgewichtszustand erreicht, bei dem die Konzentration nicht mehr weiter anwächst, also die oft verwendete „Netto-Null“ Situation.

Mit den aktuellen Emissionen von 4.7 ppm wäre „Netto-Null“ bei 515 ppm, während sich beim „Stated-Policies“ Emissionsscenario der Internationalen Energieagentur (IEA), das eine leichte Reduktion von 3% pro Dekade in der Zukunft vorsieht, ein Gleichgewicht bei 475 ppm einstellt, wie in der obigen Publikation beschrieben. Mit den Prognosedaten der IEA wird dies voraussichtlich 2080 der Fall sein:

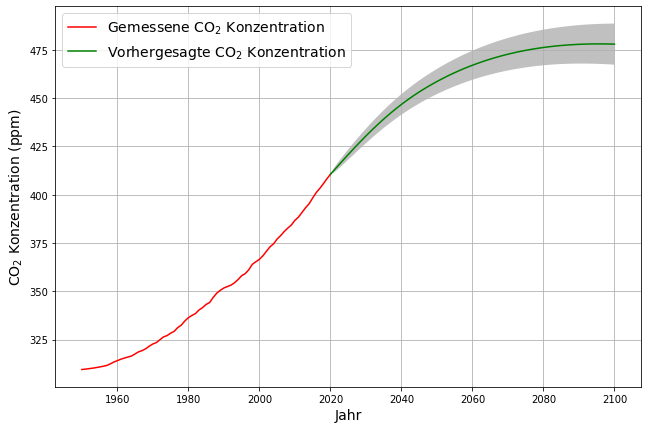
Demnach sind konstante Emissionen eine hinreichende Begründung für einen konvexen Verlauf der CO₂-Konzentration, wie wir ihn seit 2016 vorfinden. Gleichzeitig wird damit belegt, dass CO₂-Absorptionen in der Tat mit zunehmender Konzentration zunehmen.