Temperaturabhängigkeit der natürlichen CO2 Quellen und Senken

Bei dem in diesem Blog und anderswo publizierten einfachen Modell der CO₂-Senken und der natürlichen Emissionen tauchte in der Diskussion darüber immer wieder die Frage auf: Wie wird die — offensichtliche — Temperaturabhängigkeit der natürlichen CO₂-Quellen, beispielsweise die ausgasenden Ozeane, oder der Senken wie die Photosynthese, berücksichtigt? Denn in dem Modell kommt keine langfristige Temperaturabhängigkeit vor, allenfalls ein kurzfristig zyklische. Ein langfristiger Trend der Temperaturabhängigkeit ist in den letzten 70 Jahren auch bei sorgfältiger Analyse nicht erkennbar.
In der zugrunde liegenden Publikation wurde ausgeschlossen, dass der Absorptionskoeffizient temperaturabhängig sein kann (Kapitel 2.5.3). Allerdings blieb dabei offen, ob nicht doch eine direkte Temperaturabhängigkeit der Quellen oder Senken möglich ist. Und warum diese nicht aus der statistischen Analyse erkennbar ist. Dies wird in dem vorliegenden Beitrag behandelt.

Ursprüngliches temperaturunabhängiges Modell

Die vereinfachte Form der CO₂ Massenerhaltung in der Atmosphäre (siehe Gleichungen 1,2,3 der Publikation) mit anthropogenen Emissionen im Jahre , den sonstigen, überwiegend natürlichen Emissionen (zur Vereinfachung werden die Landnutzungsemissionen den natürlichen Emissionen zugeschlagen), dem Zuwachs des CO₂ in der Atmosphäre ( ist atmosphärische CO₂ Konzentration) und den Absorptionen ist:

Die Differenz der Absorptionen und der natürlichen Emissionen wurde linear modelliert mit einem konstanten Absorptionskoeffizienten und einer Konstante für die jährlichen natürlichen Emissionen:

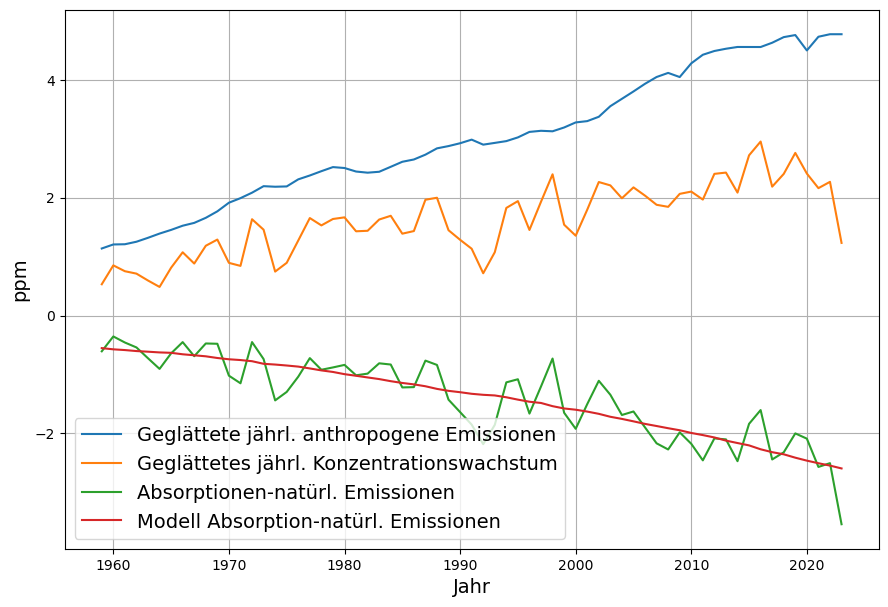
Während die Absorptionskonstante und der lineare Zusammenhang zwischen Absorption und Konzentration physikalisch sehr gut begründet und belegt ist, erscheint die Annahme der konstanten natürlichen Emissionen willkürlich. Daher ist es erhellend, statt eines konstanten Ausdrucks stattdessen aus den Messdaten und der berechneten Absorptionskonstanten das Residuum

zu betrachten:

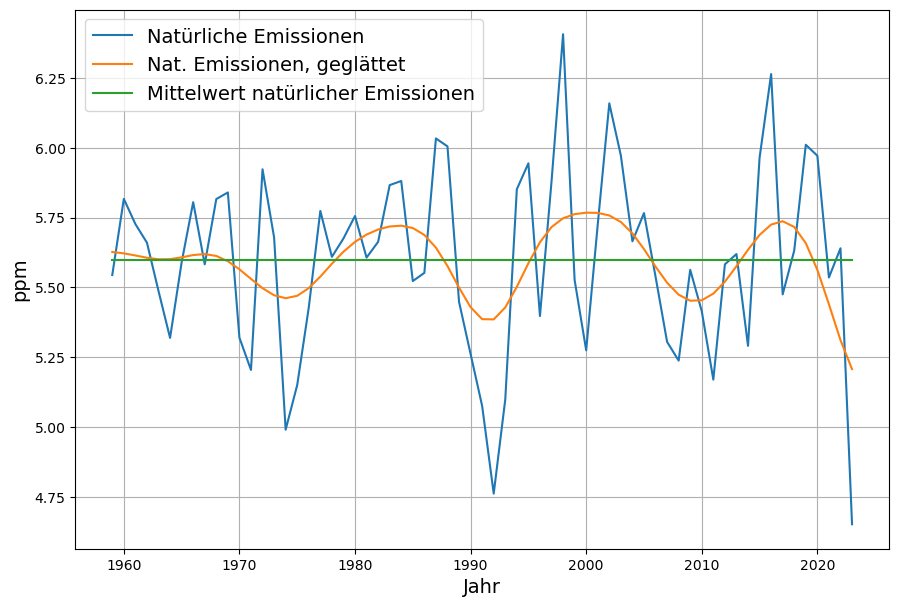
Der Mittelwert von ergibt den konstanten Modellterm . Mit einer leichten Glättung ergibt sich ein periodischer Verlauf. Roy Spencer hat diese Schwankungen mit dem El Nino begründet, wobei nicht eindeutig ist, ob die Schwankungen den Absorptionen oder den natürlichen Emissionen zuzuordnen sind. Aber es ist keinerlei langfristiger Trend erkennbar. Daher ist die Frage zu klären, warum zwar kurzfristige Temperaturabhängigkeiten vorhanden sind, aber die langfristige globale Erwärmung im Modell anscheinend keine Entsprechung hat.

Temperaturabhängiges Modell

Nun erweitern wir das Modell, indem wir sowohl für die Absorptionen als auch für die natürlichen Emissionen zusätzlich eine lineare Temperaturabhängigkeit zulassen. Da unsere Messdaten nur deren Differenz liefern, können wir die Temperaturabhängigkeit dieser Differenz in einer einzigen linearen Funktion der Temperatur , also darstellen. Gesetzt den Fall, dass sowohl also auch temperaturabhängig sind, ist die Differenz der dazugehörigen linearen Ausdrücke wieder einen linearen Ausdruck. Demnach hat das erweiterte Modell diese Gestalt.

Im Prinzip könnten und zu einer einzigen Konstanten zusammengefasst werden. Da aber von der verwendeten Temperaturskala abhängt, und von der Maßeinheit der CO₂ Konzentration, belassen wir es bei 2 Konstanten.

CO₂ Konzentration als Proxy für Temperatur

Wie bereits in der Publikation im Kapitel 2.3.2 dargelegt, gibt es zwischen der CO₂-Konzentration und der Temperatur einen Zusammenhang mit hoher Korrelation. Woher dieser Zusammenhang kommt, d.h. ob es einen kausalen Zusammenhang gibt (und in welcher Richtung) ist für diese Untersuchung unerheblich. Allerdings stellen wir hier nicht den Zusammenhang zwischen und her, sondern den zwischen (Temperatur) und (CO₂ Konzentration ohne Logarithmus).

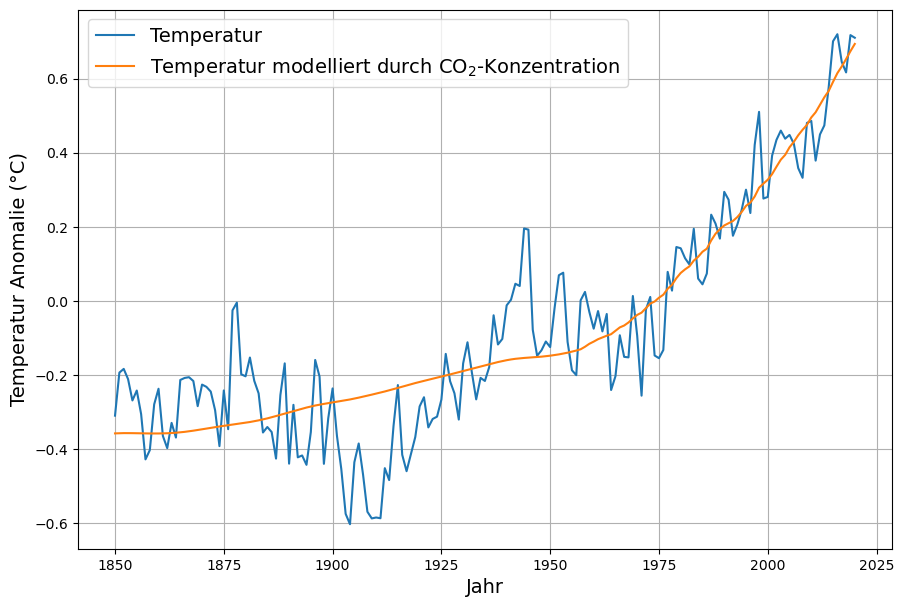
Demzufolge kann die Temperatur-Anomalie aus der Konzentration mit der linearen Funktion

mit

approximiert werden.

Verwendung des CO₂-Proxy in der temperaturabhängigen Gleichung

Setzt man für die Temperatur deren Proxy-Funktion in die temperaturabhängige Gleichung ein, so ergibt sich folgende Gleichung:

bzw.

Der Ausdruck auf der rechten Seite hat jetzt wieder die gleiche Gestalt wie die ursprüngliche Gleichung, also

mit

Schlussfolgerungen

Daher können bei einer linearen Abhängigkeit der Temperatur von der CO₂-Konzentration Temperatureffekte der Senken und Quellen nicht von Konzentrationseffekten unterschieden werden, beide gehen in die „effektive“ Absorptionskonstante und die Konstante der natürlichen Emissionen ein. Daher enthält das einfache lineare Quellen- und Senkenmodell sämtliche linearen Temperatureinflüsse.
Das erklärt die erstaunliche Unabhängigkeit des Modells von der globalen Temperaturerhöhung der letzten 70 Jahre.
Außerdem legt dieser Zusammenhang nahe, dass sich das Absorptionsverhalten der beiden atmosphärischen Senken auch in Zukunft nicht ändert.

Will man allerdings wissen, wie sich die Temperatur genau auf die Quellen und Senken auswirkt, müssen andere Datenquellen herangezogen werden. Für die Prognose künftiger CO₂-Konzentration aus anthropogenen Emissionen ist dieses Wissen aufgrund des gefundenen Zusammenhangs nicht notwendig, vorausgesetzt der lineare Zusammenhang zwischen Temperatur und CO₂-Konzentration bleibt uns noch eine Weile erhalten.