Der Senkeneffekt der A-Bombentests und das Diffusionsmodell

Dies ist ein Versuch, den gemessenen Senkeneffekt des $^{14}$ C nach dem Jahr 1963 mit dem Diffusionsmodell der Tiefsee nach Siegenthaler und Oeschger in Einklang zu bringen. Um Missverständnisse auszuschließen, wird hier nicht das vollständige Modell behandelt, sondern nur ein einziger Teilprozess betrachtet, nämlich der Diffusionsprozess der Aufnahme von CO $_2$ in den tiefen Ozean. Andere Prozesse wie Emissionen durch Ausgasung, Phytoplankton und eventuelle Temperaturabhängigkeiten bleiben unberücksichtigt. Die Landpflanzen werden durch eine grobe Abschätzung berücksichtigt.

Die Messdaten des Bombentests

In diesem Preprint zeigt John Reid aufgrund der $^{14}$ C-Messungen in der Atmosphäre durch Darstellung der atmosphärischen $^{14}$ C Konzentration auf einer logarithmischen Skala, dass die Absorption von $^{14}$ C nach 1963 ein Prozess 1. Ordnung ist, d.h. die Zerfallsrate des atmosphärischen $^{14}$ C ist strikt proportional zur Konzentration, und daraus ergibt sich ein exponentieller Zerfall:

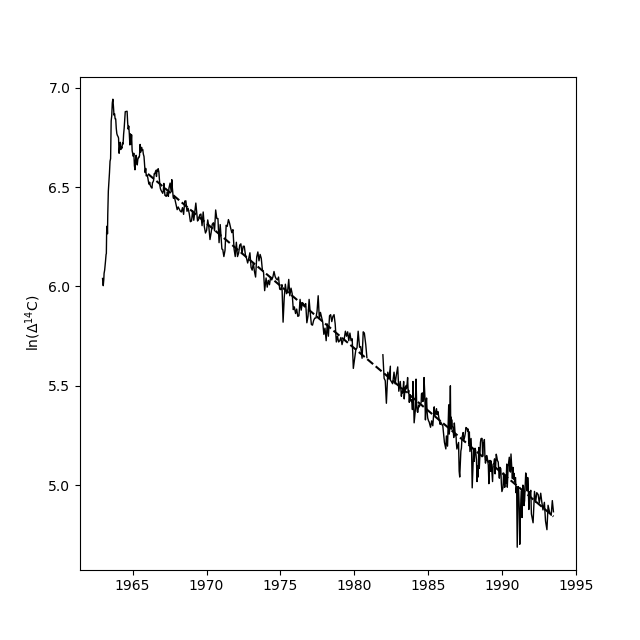
Durch lineare Regression ergibt sich aus der logarithmischen Repräsentation eine Abkling-Halbwertszeit von 11 Jahren (Zeitkonstante $\tau = 15.9$ Jahre), über einen Zeitraum von 30 Jahren ohne Sättigungseffekt.

Das $^{14}$ C dringt aber nicht nur in die 75m dicken Deckschicht des Ozeans ein, denn die Zeitkonstante für den Austausch zwischen Atmosphäre und Deckschicht ist maximal 2 Jahre. Die Messungen ergeben aber ganz klar eine Zeitkonstante von 15,9 Jahren.
Demzufolge entspricht die Zeitkonstante des atmosphärischen Zerfalls der CO $_2$ -Aufnahme in die Tiefsee. Und da $^{14}$ C bei den physikalischen Transportmechanismen nicht anders behandelt wird als $^{12}$ C und $^{13}$ C, können wir davon ausgehen, dass die Senkenwirkung für das gesamte CO $_2$ die gleiche ist wie für das $^{14}$ C-haltige. Wir können also die Messdaten der Senkenwirkung des $^{14}$ C auf das gesamte CO $_2$ hochrechnen.

Daraus ergibt sich, dass der jährliche Senkeneffekt für $^{14}$ C $1/15.9 = 6,3\%$ der über der Gleichgewichtskonzentration hinausgehenden CO $_2$ Konzentration sein muß.
Davon muß der Verdünnungseffekt abgezogen werden, der dadurch zustande kommt, dass das anthropogene CO $_2$ aus fossilen Quellen stammt, das so gut wie kein $^{14}$ C enthält. Wir gehen also davon aus dass der komplette Konzentrationsanstieg zur $^{14}$ C-Verdünnung führt. Wenn wir den Zeitraum 1960-1990 betrachten liegt 1975 grade in der Mitte. Der mittlere Konzentrationsanstieg 1975 war etwa 1.4 ppm/Jahr bei einer CO $_2$ -Konzentration von 330 ppm, das sind 0.4%/Jahr. Daher reduziert sich der tatsächliche Senkeneffekt nach Abzug dieser Verdünnung auf 5.9%/Jahr.

Weiterhin müssen wir davon ausgehen, dass ein Teil des $^{14}$ C von der Landsenke absorbiert wurde. Es zählt aber nur der Teil, der über die Saison hinaus dauerhaft gebunden bleibt. Dieser „Netto“-Anteil ergibt sich aus der in dieser Graphik dargestellten Landsenke:

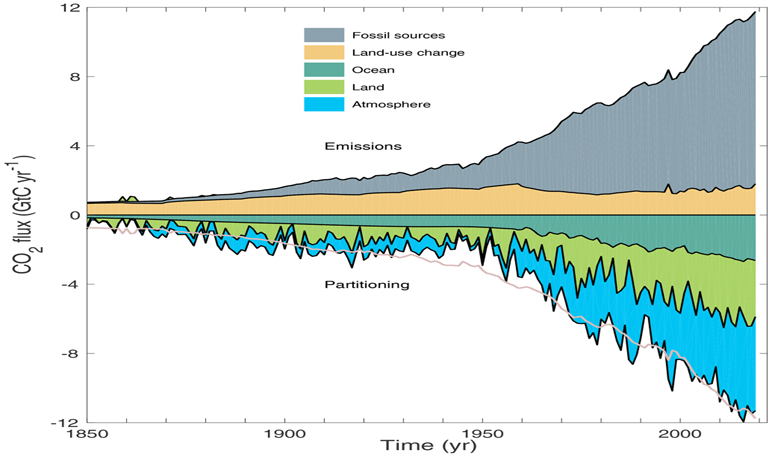
Vom gesamten Netto-Senkeneffekt von etwa 2% der über die Gleichgewichtskonzentration hinausgehenden Konzentration ist der Anteil der Landsenke etwas mehr als die Hälfte, also im Schnitt etwa 1.2%. Für den Senkeneffekt in die Ozeane verbleiben dann noch 4.7%.

Es ist nicht verwunderlich, dass die Senkenwirkung für den einmaligen $^{14}$ C-Impuls größer ist als die Netto-Senkenwirkung unter Berücksichtigung aller Prozesse. Denn wir ignorieren hier alle natürlichen Emissionen in Form von CO $_2$ -Ausgasungen aus den Ozeanen („upwelling“), denn diese enthalten kein zusätzliches $^{14}$ C.
1963 war die CO $_2$ Konzentration 320 ppm. Wir gehen also konservativerweise davon aus, dass der jährliche Senkeneffekt 1963 in den Ozean $S$ 4.7% der Differenz 320ppm – 280 ppm gewesen war.

(1) $\begin{eqnarray*}S^{global}&=& 0.047*(320-280) ppm/a\\&=&1.88 ppm/a\\&=&1.88\cdot 2.12GtC/a\\&\approx&4 GtC/a\end{eqnarray*}$

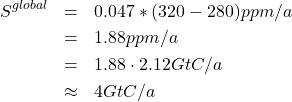
Die gesamte Meeresoberfläche beträgt etwa (71% der gesamten Erdoberfläche):
$0.71 \cdot 510\cdot 10^{12} m^2 = 362\cdot 10^{12} m^2$ .
Pro $m^2$ war 1963 der jährlich vom Meer aufgenommene Senkenfluss $F$ des CO $_2$ aufgrund der Bombentestdaten demnach
$F(C)_{1963}=\frac{4\cdot 10^{15}g/a}{362\cdot 10^{12}m^2} = 11 \frac{g}{m^2\cdot a}$

Generell ist bei einer atmosphärischen Konzentration $C^{Atmosphäre}$ der aufgrund der $^{14}$ C-Messdaten notwendigerweise vom Meer aufzunehmende Senkenfluss pro Quadratmeter:

(2) $\begin{equation*}F(C)=0.047\cdot (C^{Atmosphäre}-280 ppm)\cdot\frac{2.12\cdot 10^{15}g}{ppm}\frac{1}{362\cdot 10^{12}m^2}\end{equation*}$

Annahmen für das weitere Vorgehen

Zum Weiterrechnen müssen einige Annahmen über die Deckschicht und den tiefen Ozean getroffen werden:

Die Deckschicht erstreckt sich bis in die Tiefe von 75 m, hat also ein Volumen von etwa
$362\cdot 10^{12}m^2\cdot 75 m = 27.2\cdot 10^{15} m^3$
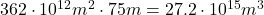
Die Deckschicht enthält heute 900 PgC¹, pro Kubikmeter also $\frac{900\cdot 10^{15}g}{27.2\cdot 10^{15}m^3}=33 \frac{g}{m^3}$
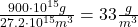
Die Deckschicht ist durch die turbulente Durchmischung im Konzentrationsgleichgewicht mit der Atmosphäre. Die heutige Konzentration in der Deckschicht entspricht also der atmosphärischen Konzentration von 420 ppm.
Demnach enthielt die Deckschicht zu Beginn der Industrialisierung bei einer atmosphärischen Konzentration von 280 ppm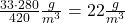
$\frac{33\cdot 280}{420}\frac{g}{m^3} = 22 \frac{g}{m^3}$
und 1963 bei 320 ppm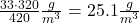
$\frac{33\cdot 320}{420}\frac{g}{m^3} = 25.1 \frac{g}{m^3}$
Allgemein erfolgt die Umrechnung der atmosphärischen Konzentration in die Deckschichtkonzentration mit:
(3) $\begin{equation*} $C^{Deckschicht} =33\frac{g}{m^3} \cdot \frac{C^{Atmosphäre}}{420 ppm} \end{equation*}$
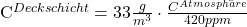
Die Ozeane sind im Schnitt etwa 3700 m tief. Daher ergibt sich für die Tiefsee eine Tiefe von 3625 m.

Modellierung der Tiefsee mit dem Diffusionsmodell

Aus den Voraussetzungen, dass

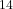sich das gesamte CO $_2$ bezüglich des Senkeneffekts genauso verhält wie das $^{14}$ C-haltige,
der Eintrag des „Bomben- 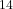$^{14}$ C“ als einmaliger Impuls betrachtet werden kann,
die Deckschicht als gut gemischt mit der Atmosphäre betrachtet werden kann,

folgt, dass wir bei der Diffusion in der Tiefsee einen CO $_2$ -Fluss gemäß Gleichung 2 aus der Deckschicht in die Tiefsee über mindestens einen Zeitraum von 30 Jahren ab 1963 garantieren müssen.

Dieser Fluss in das Diffusionssystem ist mit diskreten Koordinaten definiert als²
$F_{md} = - D\cdot\frac{\Delta C}{\Delta z}$
Als Diffussionskonstante wird zunächst wie im Berner Modell $D=3900 \frac{m^2}{a}$ angenommen.

Es wird eine diskrete Approximation der Diffusionsgleichung verwendet:
$C(t+1,z) = C(t,z) + s\cdot(C(t,z+1)-2C(t,z)+C(t,z-1))$
Mit der algorithmisch robusten Wahl der Diffusionszahl $s=0.25$ ergibt sich die besonders einfache und intuitive Form
$C(t+1,z)=0.25\cdot C(t,z+1) + 0.5\cdot C(t,z) + 0.25\cdot C(t,z-1)$

Am Rand werden 2 Fälle unterschieden:

Da die oberen Werte, also für 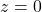$z=0$ , aus der Deckschicht vorgegeben sind, entfällt die Berechnung von $C(t+1,0)$ .
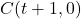Am unteren Rand wird die Neumann-Randbedingung mit 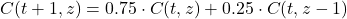$C(t+1,z)= 0.75\cdot C(t,z) + 0.25\cdot C(t,z-1)$ realisiert.

Der Zusammenhang zwischen der Diffusionszahl $s$ und der Diffusionskonstanten $D$ der allgemeinen Diffusionsgleichung ist
$s = D\cdot\frac{\Delta t}{\Delta z^2}$

Daraus ergibt sich mit $\Delta t = 1 a$ , $s=0.25$ und $D= 3900 \frac{m^2}{a}$ die räumliche Granularität $\Delta z$ :
$\Delta z = \sqrt{\frac{D}{s}\cdot \Delta t} = 2\cdot \sqrt{D\cdot\Delta t } = 2\cdot\sqrt{3900\cdot 1} m \approx 125 m$ .
Wenn bei sehr großen Diffusionskonstanten die Granularität von $z$ zu groß ist, kann dies durch Verkleinerung von $\Delta t$ und entsprechend mehr Iterationen kompensiert werden

Simulation vor und bis 30 Jahre nach den Bombentests

Bei Beginn des untersuchten Zeitraums 1963 gab es bereits anthropogene Einträge und daher war zu diesem Zeitpunkt der tiefe Ozean nicht mehr im Initialzustand der konstanten Konzentration von 22 $\frac{g}{m^3}$ . Deswegen muss das Diffusionsmodell im vorindustriellen Gleichgewichstszustand bei 280 ppm bzw. 22 $\frac{g}{m^3}$ in der Deckschicht gestartet werden.

Als Input des Diffusionsmodells werden die Konzentrationsdaten der Deckschicht verwendet, von 1850-1993 (30 Jahre nach dem Ende der Bombentests):

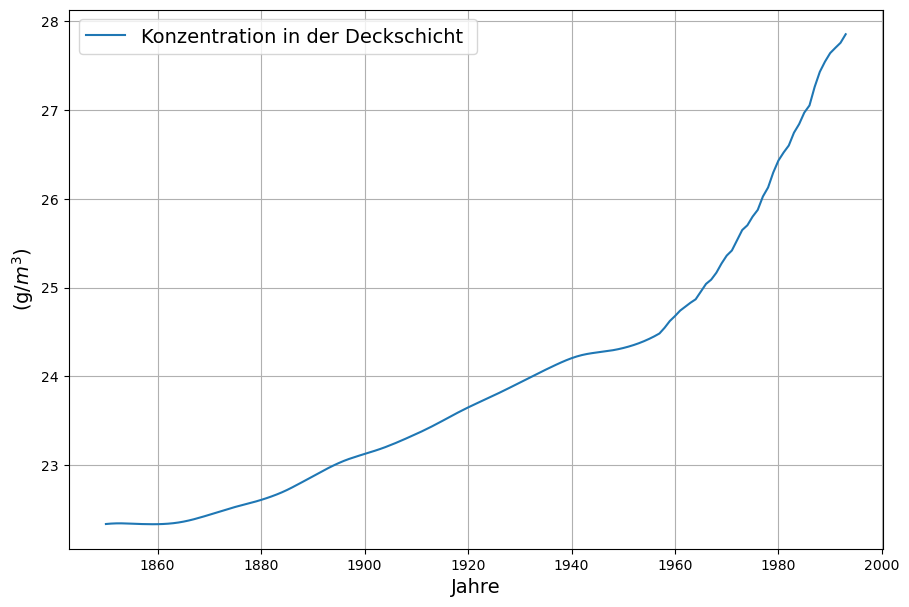
Mit der Diffusionskonstante $D=3900 m^2/a$ wird allerdings der für den $^{14}$ C-Senkeneffekt notwendige Fluss aus der Deckschicht in das Diffusionssystem der Tiefsee nicht erreicht:

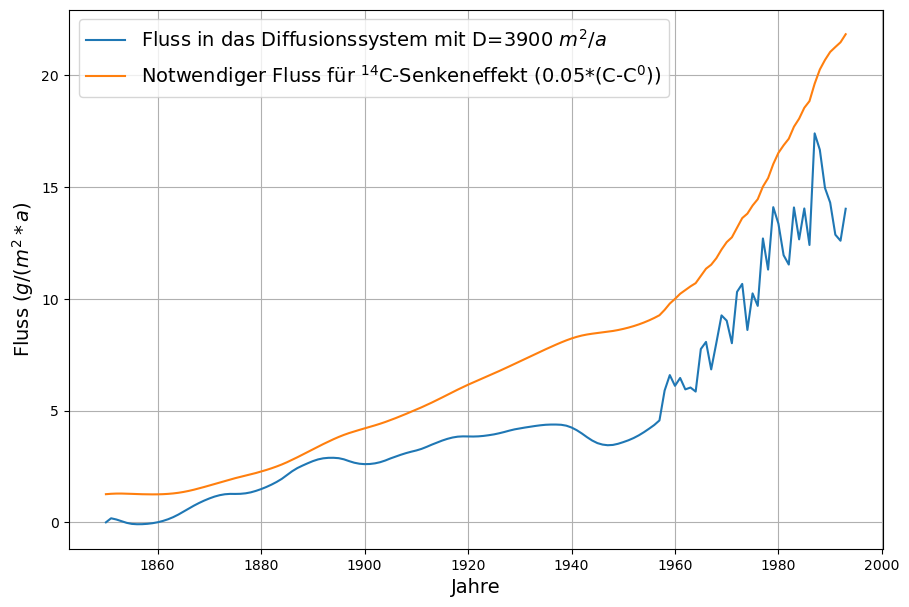
Anders ist es mit der Diffusionskonstante $D=10000 m^2/a$ . Damit stimmt der Fluss in das Diffusionssystem der Tiefsee mit dem notwendigen Fluss für den $^{14}$ C-Senkeneffekt in den Jahren 1963-1993 hinreichend überein.

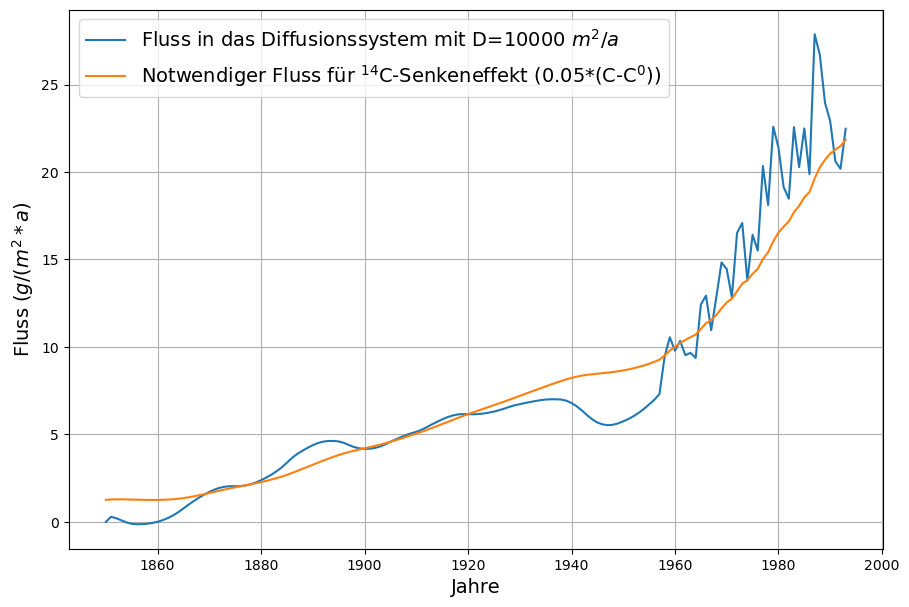
In der Arbeit „Uncertainties of predictions of future atmospheric CO₂ concentrations“ haben H. Oeschger und M. Heimann den Wert $D=10000 m^2/a$ bereits als Möglichkeit in Erwägung gezogen. Dieser Wert ist mit den atmosphärischen $^{14}$ C-Meßdaten kompatibel, im Gegensatz zu dem in sonstigen Publikationen des Berner Modells verwendeten Wert von $D=3900 m^2/a$ .

Es wäre von großem Interesse zu wissen, wie sich die Änderung der Diffusionskonstanten zu $D=10000 m^2/a$ auf die Prognosen des Berner Modells auswirken wird.

Simulationen des atmosphärischen CO2 mit einem einfachem globalen Kohlenstoffmodell, Martin Heimann,April 2024 (private Kopie) ↩︎
Simulationen des atmosphärischen CO2 mit einem einfachem globalen Kohlenstoffmodell, Martin Heimann,April 2024 (private Kopie) ↩︎