Die zentrale Frage der ganzen Klimadiskussion dreht sich um ein einziges Thema: Wie ändert sich das Klima, insbesondere die Welt-Durchschnittstemperatur, wenn sich der ![]() -Gehalt der Atmosphäre verdoppelt. Dies nennt man die sogenannte Klima-Sensitivität, die Stellschraube aller Klimapolitik. Ausgehend von den unterschiedlichen Modellvorstellungen des Internationalen Klimarates, des IPCC, droht uns bis Ende des Jahrhunderts eine durchschnittliche Temperaturerhöhung von 2°-5° C. Das politische „Optimalziel“ des Pariser Klimaabkommens ist eine Beschränkung auf 1.5° C.
-Gehalt der Atmosphäre verdoppelt. Dies nennt man die sogenannte Klima-Sensitivität, die Stellschraube aller Klimapolitik. Ausgehend von den unterschiedlichen Modellvorstellungen des Internationalen Klimarates, des IPCC, droht uns bis Ende des Jahrhunderts eine durchschnittliche Temperaturerhöhung von 2°-5° C. Das politische „Optimalziel“ des Pariser Klimaabkommens ist eine Beschränkung auf 1.5° C.
Das Problem ist, dass die sich daraus ergebenden Vorgaben hinsichtlich ![]() -Vermeidung auf einer angenommenen Klimasensitivität von 2°-3° C bei Verdopplung des
-Vermeidung auf einer angenommenen Klimasensitivität von 2°-3° C bei Verdopplung des ![]() -Gehaltes beruhen.
-Gehaltes beruhen.
Ist das korrekt? Ungeheure Kosten, der Industriestandort Deutschland und die dadurch bedingte Verarmung, nicht zuletzt unsere Freiheit hängen von der richtigen Antwort auf diese Frage ab.
Ein einfaches Klimamodell
Wir wollen die bewährte MODTRAN-Simulation als eindimensionales Mini-Klimamodell verwenden, um die Frage der Klima-Sensitivität zu beantworten. Diese Vereinfachung ist insofern legitim, weil das Strahlungsgleichgewicht im Prinzip an jedem Ort der Erde berechnet werden kann und wenn unter den verschiedenen Bedingungen ein konsistentes Endergebnis herauskommt, dann halten wir es für verlässlich. Das Programm ist öffentlich zugänglich, daher ist alles überprüfbar. Wir wollen uns heute auf eine Beispielrechnung mit der Standardatmosphäre beschränken.
Dazu stellen wir das MODTRAN Programm so ein, wie die Atmosphäre 1850 etwa gewesen war, insbesondere war der ![]() Gehalt damals 280 ppm. Alle anderen Luftbestandteile bleiben auf dem voreingestellten „Standard“-Durchschnittswert. Das Atmosphärenmodell ist die sogenannte US Standard-Atmosphäre, wie sie auch in der Internationalen Luftfahrt verwendet wird. Als Wolkenmodell habe ich diejenigen Wolken gewählt, die am häufigsten vorkommen, die Cumulus-Wolken zwischen 660m und 2700m Höhe. Der Wasserdampfgehalt wird dann so eingestellt, dass die Infrarot-Abstrahlung gerade den korrekten Wert von etwa 240
Gehalt damals 280 ppm. Alle anderen Luftbestandteile bleiben auf dem voreingestellten „Standard“-Durchschnittswert. Das Atmosphärenmodell ist die sogenannte US Standard-Atmosphäre, wie sie auch in der Internationalen Luftfahrt verwendet wird. Als Wolkenmodell habe ich diejenigen Wolken gewählt, die am häufigsten vorkommen, die Cumulus-Wolken zwischen 660m und 2700m Höhe. Der Wasserdampfgehalt wird dann so eingestellt, dass die Infrarot-Abstrahlung gerade den korrekten Wert von etwa 240 ![]() bekommt. Das ist mit einem durchschnittlichen relativen Wasserdampfgehalt von 0.25 gegeben. Die angenommene Durchschnitts-Oberflächentemperatur der Standardatmosphäre ist 15.2° C.
bekommt. Das ist mit einem durchschnittlichen relativen Wasserdampfgehalt von 0.25 gegeben. Die angenommene Durchschnitts-Oberflächentemperatur der Standardatmosphäre ist 15.2° C.
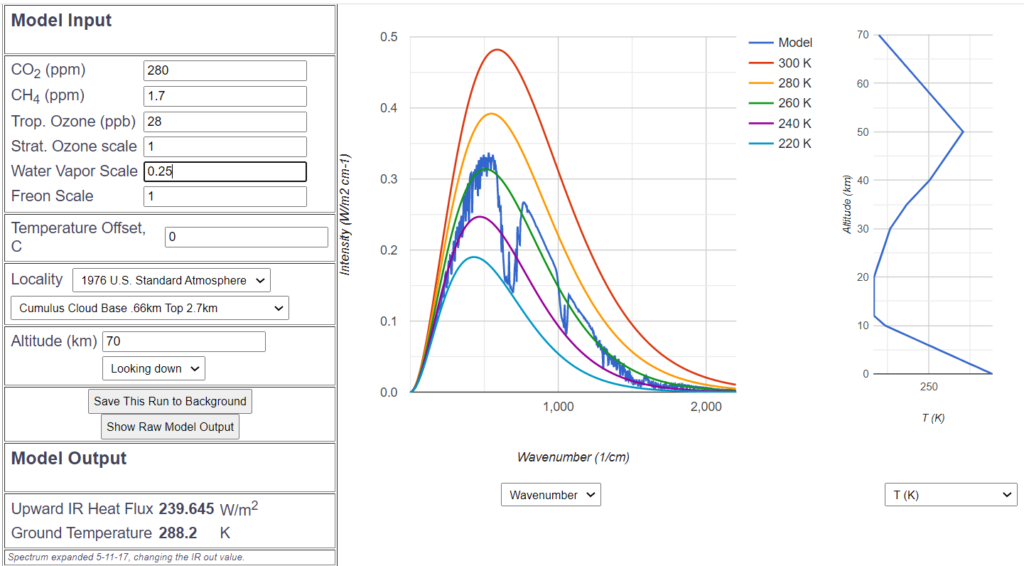
Das dunkelblaue Spektrum zeigt das bereits besprochene Verhalten. Das ![]() -Loch ist sehr ähnlich wie wir es schon kennen, der Einfluss des Wasserdampfes am rechten und am linken Rand ist ebenfalls gut erkennbar. Als Hilfslinien sind zusätzlich die Kurven eingetragen, die das ideale Strahlungsverhalten ohne Treibhausgase bei den Temperaturen 220° K bis 300° K kennzeichnen. Damit kann man die Abstrahltemperatur und damit die Energie an jeder Stelle des Spektrums schätzen.
-Loch ist sehr ähnlich wie wir es schon kennen, der Einfluss des Wasserdampfes am rechten und am linken Rand ist ebenfalls gut erkennbar. Als Hilfslinien sind zusätzlich die Kurven eingetragen, die das ideale Strahlungsverhalten ohne Treibhausgase bei den Temperaturen 220° K bis 300° K kennzeichnen. Damit kann man die Abstrahltemperatur und damit die Energie an jeder Stelle des Spektrums schätzen.
Als nächsten Test wollen wir den heutigen ![]() -Gehalt von 415 ppm einstellen. Die Kurve von 1850 bleibt als blaue Referenz-Kurve im Hintergrund, und die rote Kurve von heute wird „darüber“ gezeichnet.
-Gehalt von 415 ppm einstellen. Die Kurve von 1850 bleibt als blaue Referenz-Kurve im Hintergrund, und die rote Kurve von heute wird „darüber“ gezeichnet.
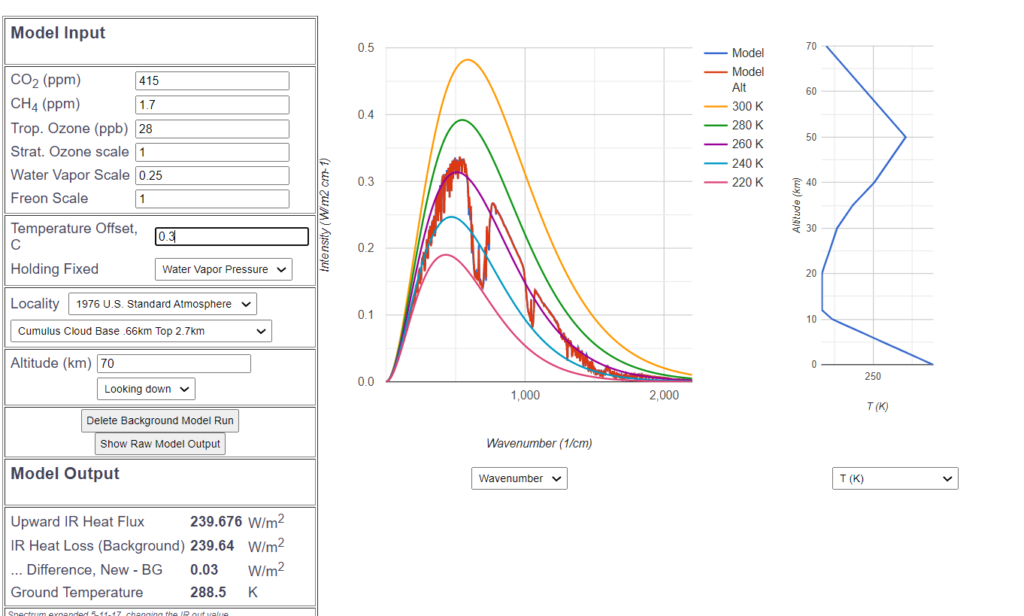
Was als erstes auffällt, ist, dass die Kurven fast identisch sind, und mit bloßem Auge nicht zu unterscheiden. Die rote Kurve verdeckt die blaue fast vollständig. Nur in den berechneten Werte links sieht man einen leichten Unterschied. Die um etwa 1 ![]() geringere Abstrahlung wird durch eine Temperaturerhöhung der Erdoberfläche von 0.3° kompensiert. Diese durchschnittlich 0.3° sind der effektive Treibhauseffekt seit Beginn der Industrialisierung bis heute, aufgrund des weithin akzeptierten MODTRAN Modells.
geringere Abstrahlung wird durch eine Temperaturerhöhung der Erdoberfläche von 0.3° kompensiert. Diese durchschnittlich 0.3° sind der effektive Treibhauseffekt seit Beginn der Industrialisierung bis heute, aufgrund des weithin akzeptierten MODTRAN Modells.
Wie ist es nun, wenn wir eine Verdoppelung des ![]() Gehaltes von 280 ppm auf 560 ppm annehmen? Wiederum wird die neue Kurve der ursprünglichen blauen Kurve überlagert.
Gehaltes von 280 ppm auf 560 ppm annehmen? Wiederum wird die neue Kurve der ursprünglichen blauen Kurve überlagert.
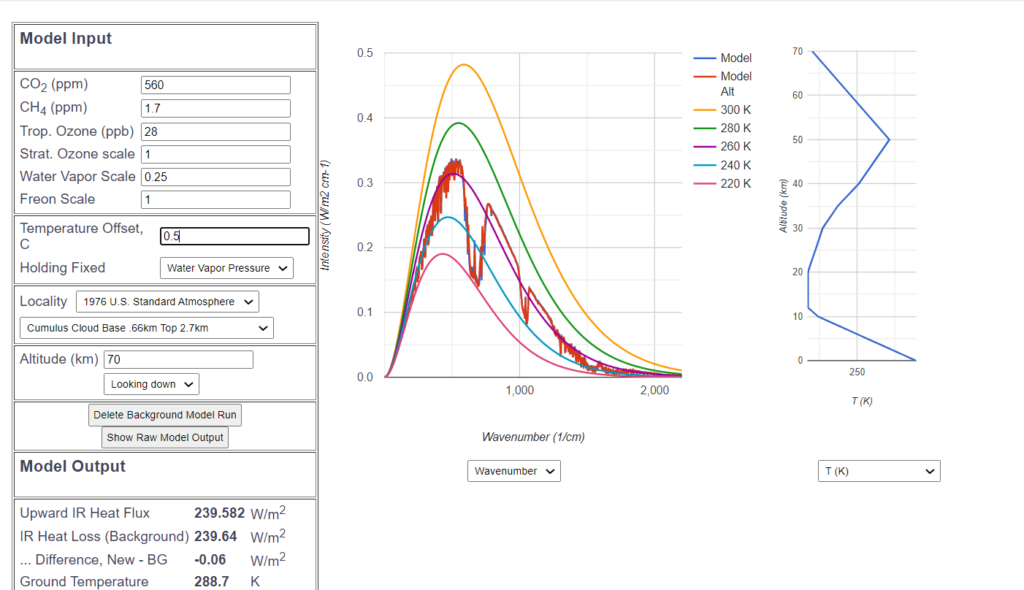
Und wiederum sind mit bloßem Auge kaum Unterschiede zu erkennen – einige kleine blaue Spitzen schauen bei der Wellenzahl 500 heraus, und die „![]() „-Wanne ist einen Hauch breiter geworden. Um die aufgrund dieses minimalen Treibhauseffektes verminderte Infrarot-Abstrahlung zu kompensieren, wird die Bodentemperatur um insgesamt 0.5° C erhöht. Damit beträgt die Klimasensitivität mit der vorgenommenen MODTRAN Simulation ziemlich genau ein halbes Grad. Ein mögliches Erklärungsmodell für diese gemessene Sensitivität wird in diesem Artikel beschrieben.
„-Wanne ist einen Hauch breiter geworden. Um die aufgrund dieses minimalen Treibhauseffektes verminderte Infrarot-Abstrahlung zu kompensieren, wird die Bodentemperatur um insgesamt 0.5° C erhöht. Damit beträgt die Klimasensitivität mit der vorgenommenen MODTRAN Simulation ziemlich genau ein halbes Grad. Ein mögliches Erklärungsmodell für diese gemessene Sensitivität wird in diesem Artikel beschrieben.
Demnach besteht keinerlei Grund zu irgendeinem Alarmismus. Dieser Wert ist weit unterhalb der niedrigsten Annahmen des Weltklimarates.
Warum kommt der Weltklimarat zu anderen Ergebnissen
Die natürliche Frage nach diesen Überlegungen ist, warum der Weltklimarat, in dem ja die besten Klimaforscher vertreten sind, zu so viel pessimistischeren Ergebnissen kommen?
Ein zentrales Problem dabei ist, dass deren Klimamodelle extrem komplex sind und den Anspruch haben, die gesamte Komplexität des Klimageschehens abzubilden. Es gibt gute Gründe anzunehmen, dass dies unter den heutigen Voraussetzungen grundsätzlich nicht möglich ist, z.B. weil turbulente energiereiche Phänomene wie Meeresströmungen oder Tropenstürme in diesen Modellen nicht angemessen abbildbar sind. Ähnliche Modelle werden zur Wettervorhersage verwendet, und diese versagen bekanntlich bereits häufig bei Vorhersagen, die über wenige Tage hinausgehen.
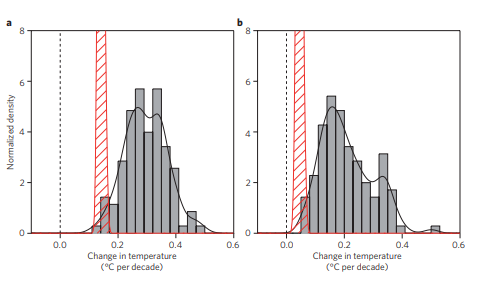
Ein wichtiger Grund, die Gültigkeit der „globalen Zirkulationsmodelle“, kurz GCM genannt, anzuzweifeln, ist der, dass sie in zurückliegenden Vorhersagen für vergangene Klimadaten zu hohe Werte vorhergesagt haben.
Links die durchschnittliche Temperaturentwicklung (roter Balken) 1993-2012 – 0.15°/10 Jahre, rechts dasselbe im Zeitraum 1998-2012 – 0.03°/10 Jahre, und dazu die Ergebnisse von 110 verschiedenen Klimamodellen. Fast alle hatten deutlich höhere Temperaturen geschätzt.
Simulation der IPCC-Annahmen
Mit dem MODTRAN Simulationsprogramm kann man aufgrund der von IPCC-nahen Autoren publizierten Daten allerdings deren Denkweise nachvollziehen. Dazu wird zunächst eine Atmosphäre ganz ohne Wasserdampf und ohne die anderen Treibhausgase angenommen, und dort die ![]() Sensitivität gemessen.
Sensitivität gemessen.
Mit der MODTRAN Simulation wird diese Situation erreicht, wenn in der Standard-Atmosphäre alles bis auf den ![]() Gehalt auf 0 gesetzt wird, also auch keine Wolken, kein Wasserdampf.
Gehalt auf 0 gesetzt wird, also auch keine Wolken, kein Wasserdampf.
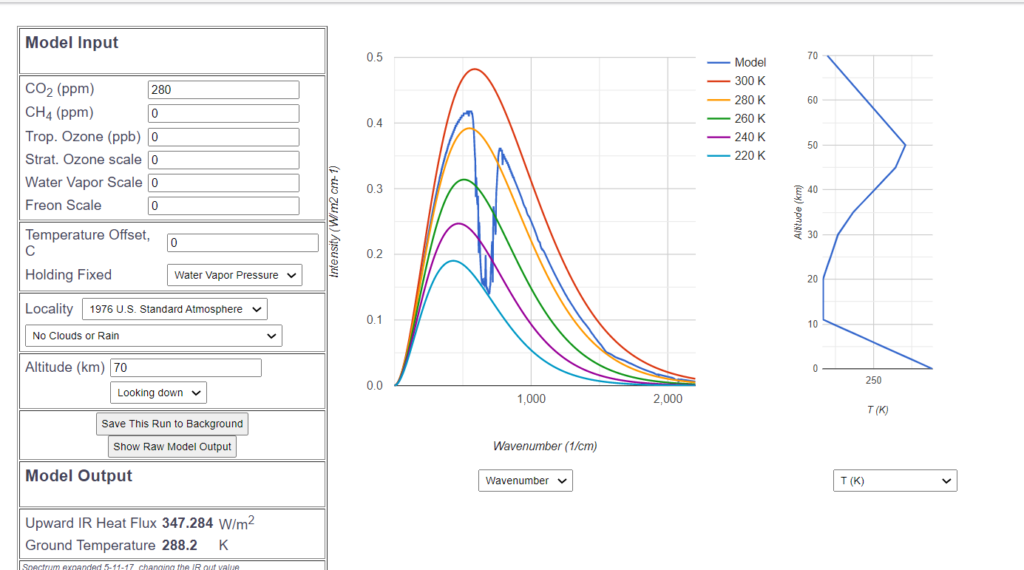
Damit steigt natürlich die hypothetische Abstrahlung auf einen unrealistisch hohen Wert von 347 ![]() . Deutlich ist als einzige Abweichung von der „Idealkurve“ das bekannte
. Deutlich ist als einzige Abweichung von der „Idealkurve“ das bekannte ![]() -Loch zu erkennen.
-Loch zu erkennen.
Bei Verdoppelung des ![]() -Gehalts und gleichbleibender Bodentemperatur sinkt aufgrund des Treibhauseffekts jetzt die Abstrahlung um 3.77
-Gehalts und gleichbleibender Bodentemperatur sinkt aufgrund des Treibhauseffekts jetzt die Abstrahlung um 3.77 ![]() .
.
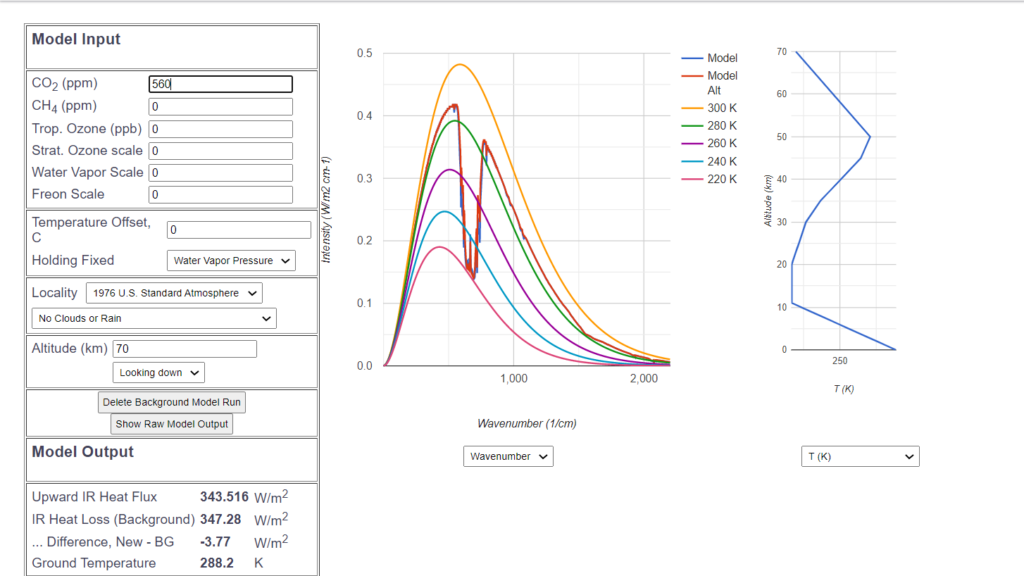
Das ist ziemlich genau der vom Weltklimarat veröffentlichte Wert des ![]() bedingten „Strahlungsantriebs“ („radiative forcings“). Die verminderte Abstrahlung wird durch Temperaturerhöhung kompensiert:
bedingten „Strahlungsantriebs“ („radiative forcings“). Die verminderte Abstrahlung wird durch Temperaturerhöhung kompensiert:
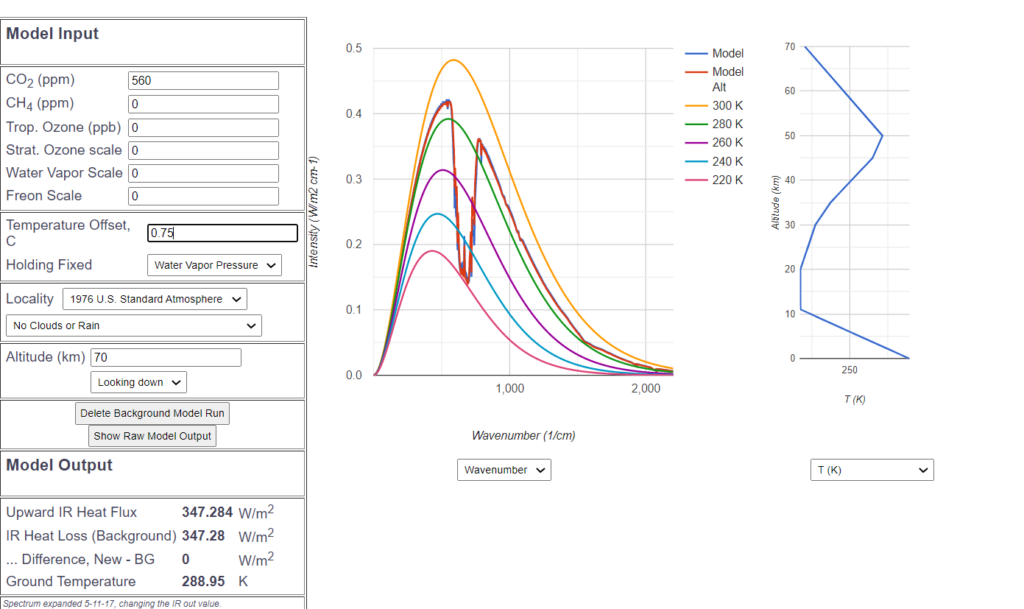
Demnach gleicht eine Temperaturerhöhung von 0.75° die Verdoppelung von ![]() wieder aus, das wäre laut MODTRAN die Sensitivität. Viele Wissenschaftler kommen allerdings auf eine noch höhere Sensitivität von etwa 1°.
wieder aus, das wäre laut MODTRAN die Sensitivität. Viele Wissenschaftler kommen allerdings auf eine noch höhere Sensitivität von etwa 1°.
Diese Sensitivität wird aber — in gewisser Weise zu Recht — von den IPCC nahen Wissenschaftlern als die „reine ![]() -Sensitivität“ bezeichnet, weil dabei noch nicht der Einfluss des Wasserdampfes berücksichtigt ist. Da aber Wasserdampf ein noch stärkeres Treibhausgas ist, und durch die
-Sensitivität“ bezeichnet, weil dabei noch nicht der Einfluss des Wasserdampfes berücksichtigt ist. Da aber Wasserdampf ein noch stärkeres Treibhausgas ist, und durch die ![]() -bedingte Temperatur-Erhöhung mehr Wasserdampf erzeugt wird, wird in dieser Denkweise die
-bedingte Temperatur-Erhöhung mehr Wasserdampf erzeugt wird, wird in dieser Denkweise die ![]() Sensitivität dadurch effektiv verdoppelt. So ist es möglich, zu einer Sensitivität von 2° zu kommen, die man dann durch andere Katastrophen-Szenarien wie das hypothetische Abschmelzen des Polareises noch willkürlich steigern kann. Völlig unberücksichtigt lassen sie dabei die Cumulus-Wolkenbildung, die ebenfalls durch Vergrößerung des Wasserdampfgehaltes verstärkt würde und die zur Reduzierung der einfallenden Energie führen würde, also zu einer starken negativen Rückkopplung. Allenfalls wird das Thema Wolken dadurch genutzt, indem argumentiert wird, dass die sehr hohen Zirrus-Wolken u.U. zu einer Verstärkung des Treibhauseffektes führen.
Sensitivität dadurch effektiv verdoppelt. So ist es möglich, zu einer Sensitivität von 2° zu kommen, die man dann durch andere Katastrophen-Szenarien wie das hypothetische Abschmelzen des Polareises noch willkürlich steigern kann. Völlig unberücksichtigt lassen sie dabei die Cumulus-Wolkenbildung, die ebenfalls durch Vergrößerung des Wasserdampfgehaltes verstärkt würde und die zur Reduzierung der einfallenden Energie führen würde, also zu einer starken negativen Rückkopplung. Allenfalls wird das Thema Wolken dadurch genutzt, indem argumentiert wird, dass die sehr hohen Zirrus-Wolken u.U. zu einer Verstärkung des Treibhauseffektes führen.
Nach meiner Auffassung ist aber das Auseinanderreißen von ![]() , Wolken und Wasserdampf bei der Berechnung der
, Wolken und Wasserdampf bei der Berechnung der ![]() Sensitivität nicht berechtigt. Werden alle Faktoren simultan berücksichtigt, führt das zu der oben genannten geringen Sensitivitität von 0.5°.
Sensitivität nicht berechtigt. Werden alle Faktoren simultan berücksichtigt, führt das zu der oben genannten geringen Sensitivitität von 0.5°.

Frage: Es wird immer nur mit Strahlung gearbeitet, ist aber in Bodennähe nicht vielmehr die Konvektion dominierend für den Wärmetransport ( wie übrigens auch im Treibhaus) ?
Da stimme ich Ihnen zu, siehe https://klima-fakten.net/?page_id=269 und https://klima-fakten.net/?p=2863&lang=en.
Aber bedenken Sie, nach Einsteins Arbeit „Zur Quantentheorie der Strahlung“ (http://hannah2.be/optische_communicatie/EINSTEIN/EINSTEIN.PDF) ist das Strahlungsgleichgewicht strikt konsistent mit dem thermodynamischen Gleichgewicht. Das erlaubt es, so zu tun, als könnte man den gesamten Energieaustausch aus der Strahlungsperspektive betrachten, obwohl de facto fast 90% des Energieaustauschs thermodynamischer Natur ist. Die Ergebnisse sind aber, sofern man es korrekt macht, die gleichen: https://ia800503.us.archive.org/21/items/RadiationPhysicsConstraintsOnGlobalWarmingCo2IncreaseHasLittleEffect/RadiationPhysicsConstraintsOnGlobalWarmingfor-submission-plus-9.pdf
Deswegen sehen Sie rechts vom MODTRAN Strahlungsdiagram ein Temperaturdiagramm. Die Temperaturen werden – zumindest in der Troposphäre – thermodynamisch bestimmt, sie dienen der Kopplung zwischen Thermodynamik und der Strahlungsphysik.
Jetzt verstehe ich Ihren Trick: Sie parametrisieren sich eine zu 100% bewölkte Erde mit einer sehr geringen Luftfeuchtigkeit zurecht, die nur diese eine Bedingung erfüllen muß: 240W/m². Kein Wunder, daß da die Wirkung von CO2 schlecht aussieht. So ersparen Sie sich immerhin das Nachdenken darüber, was es mit der „Surface Budget Fallacy“ [2 oben] auf sich hat.
An Ihrer Stelle hätte ich entweder eine gewichtete Summe aus allen simulierbaren Erdregionen gebildet (der ozeanreiche Süden fehlt in MODTRAN) oder die 25% Wolkenbedeckung so gerechnet: 0,2 * bewölktes Spektrum + 0,8 * unbewölktes Spektrum.
Dass man die Abstrahlbedingung 240 W/m^2 auf verschiedenen Wegen erreichen kann, steht außer Frage. Wie wäre es, wenn Sie sich die Mühe machen, Ihr vorgeschlagenes Szenario durchzurechnen? Als Randbedingung fordere ich nur, dass am Ende die mittlere Abstrahlung 240 W/m^2 beträgt, was der Realität (Albedo=0,3) entspricht. Ich biete Ihnen an, dies als eigenständigen Beitrag mit Ihrem Namen hier zu publizieren.
Sehr geehrter Herr Dengler,
sind Sie sicher, daß Sie für Ihre Argumentation den Bewölkungsgrad ändern müssen, indem Sie die Wassermenge in der Luft auf ein Viertel absenken?
Bei CO2 = 280ppm und „Water Vapor Scale“ = 0,25 erhalten Sie das MODTRAN-Diagramm „Simulation der vorindustriellen Atmosphäre“ mit „Upward IR Heat Flux“ = 239,65 W/m².
Auf Ihrer Hauptseite zeigen Sie bei einer vergleichbaren Ausgangssimulation, allerdings mit „Water Vapor Scale“ = 1, bei CO2 = 280ppm das MODTRAN-Diagramm „Abstrahlungsmodell für 280 ppm CO_2-Anteil (Jahr 1850)“ mit „Upward IR Heat Flux“ = 269,35 W/m².
Entsprechendes ist zu finden bei CO2 = 410ppm und 560ppm.
Wie erklären Sie die Differenz von rund 30 W/m² in der Strahlungsflußdichte bei derselben Oberflächentemperatur von 15,0°C?
Beste Grüße
Georg Nowak
Danke für diesen Hinweis. Dafür gibt es eine sehr schlichte Erklärung – die Webseiten sind historisch gewachsen, und am Anfang (das ist die „Hauptseite“) habe ich noch nicht auf jedes Detail geachtet, insbesondere noch nicht darauf, dass man für realistische Sensitivitätsbetrachtungen die reale IR-Abstrahlung verwenden muß (IPCC macht das übrigens auch nicht, für deren CO2 Sensitivität ist die Abstrahlung über 300 W/m^2, was schon allein den größten Teil des zu hohen Wertes erklärt). Um diese Unschärfen präziser zu behandeln, erstelle ich die speziellen Seiten wie z.B. die mit der Sensitivität. Die Luftfeuchtigkeit und Wolkendecke sind grade so gewählt, dass die notwendigen 240 W/m^2 als IR-Abstrahlung bei einer Bodentemperatur von 15° herauskommen. Sie können das in gewissen Grenzen variieren. Die Wolkenmodelle sind bei MODTRAN halt nicht kontinuierlich veränderbar, dadurch ist die Zahl der möglichen Kombinationen eingeschränkt – es gibt, glaube ich, nur 2 Wolkenmodelle, mit denen die 240 W/m^2 überhaupt erreichbar sind, zum Fine-Tuning bleibt dann nur noch die Luftfeuchtigkeit.
Wenn ich Zeit finde (die ist im Moment etwas knapp, weil ich an einer größeren Publikation arbeite), dann korrigiere ich die Hauptseite, damit alles wieder einigermaßen konsistent ist.
Man kann sich noch darüber streiten, ob es legitim ist, den weltweiten Mittelwert zu verwenden, ich neige aus empirischen (habe viele nicht veröffentlichte Berechnungen gemacht) und analytischen Gründen (fast alle Prozesse lassen sich hinreichend genau lokal linearisieren) dazu, das die Mittelung des Strahlungsgleichgewichts legitim ist.
Sehr geehrter Herr Dengler,
Ihre Vorgehensweise wirkt auf den Laien merkwürdig:
Sie wählen willkürlich eine Region, obwohl es um den globalen Treibhauseffekt geht. Sie senken die Luftfeuchtigkeit (Water Vapor Scale) auf ein Viertel. Sie suchen eine passende Wolkenbedeckung (Cumulus) aus, um auf eine gewünschte Ausgangssituation zu kommen.
Die Konsequenz dieser Vorgehensweise: Vollzieht man dies mit MODTRAN nach, bekommt man eine fast maximale Gegenstrahlung zu sehen, egal welche Region man für dieses Gedankenexperiment auswählt. Die Gegenstrahlung kommt dadurch zum großen Teil von der Unterseite der Wolken; die Ausgangsstrahlung Richtung Weltraum stammt von der Oberseite der Wolken und nicht vom Erdboden.
Globales Klima ist die zeitliche und räumliche Mittelung über alle Regionen auf der Erdoberfläche. Entsprechend sollte man auch rechnerisch vorgehen. Dafür gibt es Klimamodelle und Klimamodellierer.
Versuch einer Begründung, warum die Klima-Sensitivität nicht auf den CO2-Anteil reduziert werden kann – anhand einer MODTRAN-Simulation:
– Vorgaben „Tropical Atmosphere“, „Holding Fixed: Water Vapor“
– Simulation mit CO2=280ppm und CO2=560ppm.
Hierbei ändert sich die Strahlungsflußdichte sowohl oben (TOA) Richtung Weltraum als auch nach unten auf den Boden bzw. die Ozeanoberfläche. Die Landoberfläche wird durch diese Erwärmung vielleicht stellenweise trockener. Der Ozean erwärmt sich und verdunstet mehr Wasser. Konvektion bringt das Wasser in die Höhe der nun gewachsenen Troposphäre. Von dort strömt die Feuchtigkeit Richtung Pole ab (Hadley-Zelle [1]). Dies setzt sich fort mit Auswirkungen auf den gesamten Globus.
Der reale Anstieg geht nicht plötzlich vor sich. Die Steigerung von CO2-Konzentration und Erwärmung laufen stetig ab, aber mit einer Verzögerung.
Jedes nicht-kondensierende Treibhausgas wirkt sich in dieser Weise auf den Wasserhaushalt aus. CO2-Sensitivität OHNE den H2O-Beitrag abzuhandeln, ist unvollständig: „Plass and the Surface Budget Fallacy“ [2].
Es gibt Gase, die sich besonders kritisch in dieser Hinsicht verhalten: FCKW und N2O [3][4].
Beste Grüße
Georg Nowak
[1] https://de.wikipedia.org/wiki/Hadley-Zelle
[2] https://www.realclimate.org/index.php/archives/2010/01/plass-and-the-surface-budget-fallacy/
[3] https://www.heise.de/news/Ozonschicht-FCKW-Verbot-hat-noch-drastischere-Klimaerwaermung-verhindert-6169281.html
[4] https://www.lancaster.ac.uk/news/scientists-reveal-how-landmark-cfc-ban-gave-planet-fighting-chance-against-global-warming
Irgendwie haben Sie da was missverstanden. Nirgendwo ist in meinen Betrachtungen von einer speziellen Region die Rede. Weil es eine globale Betrachtung ist, habe ich die Standardatmosphäre gewählt. Welches Wolkenmodell und welche Luftfeuchtigkeit gewählt wird, ist völlig zweitrangig. Hauptsache, die global durchschnittliche Abstrahlung in den Weltraum mit 240 W/m^2 ist korrekt. Das ist mein spezifischer Beitrag in der Klimadiskussion – dieser Aspekt wird meist ignoriert, ist aber m.E. entscheidend, siehe meine Diskussion über die vom IPCC verbreitete CO2-Sensitivität. Genau dadurch kommt implizit die Bedeutung des Wasserdampfes und der Wolken zur Geltung:
– Wolkenalbedo wird berücksichtigt durch Fixierung der Abstrahlung auf 240 W/m^2
– H20 Treibhauseffekt durch Wolkenmodell und Wasserdampf-Berücksichtigung.
Über die Gegenstrahlung möchte ich an dieser Stelle nicht diskutieren. Für die mich interessierende Energiebilanz zwischen Atmosphäre und Weltraum ist die Gegenstrahlung irrelevant.