Klima-Sensitivität
[latexpage]
Die zentrale Frage der ganzen Klimadiskussion dreht sich um ein einziges Thema: Wie ändert sich das Klima, insbesondere die Welt-Durchschnittstemperatur, wenn sich der $CO_2$-Gehalt der Atmosphäre verdoppelt. Dies nennt man die sogenannte Klima-Sensitivität, die Stellschraube aller Klimapolitik. Ausgehend von den unterschiedlichen Modellvorstellungen des Internationalen Klimarates, des IPCC, droht uns bis Ende des Jahrhunderts eine durchschnittliche Temperaturerhöhung von 2°-5° C. Das politische „Optimalziel“ des Pariser Klimaabkommens ist eine Beschränkung auf 1.5° C.
Das Problem ist, dass die sich daraus ergebenden Vorgaben hinsichtlich $CO_2$-Vermeidung auf einer angenommenen Klimasensitivität von 2°-3° C bei Verdopplung des $CO_2$-Gehaltes beruhen.
Ist das korrekt? Ungeheure Kosten, der Industriestandort Deutschland und die dadurch bedingte Verarmung, nicht zuletzt unsere Freiheit hängen von der richtigen Antwort auf diese Frage ab.
Ein einfaches Klimamodell
Wir wollen die bewährte MODTRAN-Simulation als eindimensionales Mini-Klimamodell verwenden, um die Frage der Klima-Sensitivität zu beantworten. Diese Vereinfachung ist insofern legitim, weil das Strahlungsgleichgewicht im Prinzip an jedem Ort der Erde berechnet werden kann und wenn unter den verschiedenen Bedingungen ein konsistentes Endergebnis herauskommt, dann halten wir es für verlässlich. Das Programm ist öffentlich zugänglich, daher ist alles überprüfbar. Wir wollen uns heute auf eine Beispielrechnung mit der Standardatmosphäre beschränken.
Dazu stellen wir das MODTRAN Programm so ein, wie die Atmosphäre 1850 etwa gewesen war, insbesondere war der $CO_2$ Gehalt damals 280 ppm. Alle anderen Luftbestandteile bleiben auf dem voreingestellten „Standard“-Durchschnittswert. Das Atmosphärenmodell ist die sogenannte US Standard-Atmosphäre, wie sie auch in der Internationalen Luftfahrt verwendet wird. Als Wolkenmodell habe ich diejenigen Wolken gewählt, die am häufigsten vorkommen, die Cumulus-Wolken zwischen 660m und 2700m Höhe. Der Wasserdampfgehalt wird dann so eingestellt, dass die Infrarot-Abstrahlung gerade den korrekten Wert von etwa 240 $\frac{W}{m^2}$ bekommt. Das ist mit einem durchschnittlichen relativen Wasserdampfgehalt von 0.25 gegeben. Die angenommene Durchschnitts-Oberflächentemperatur der Standardatmosphäre ist 15.2° C.
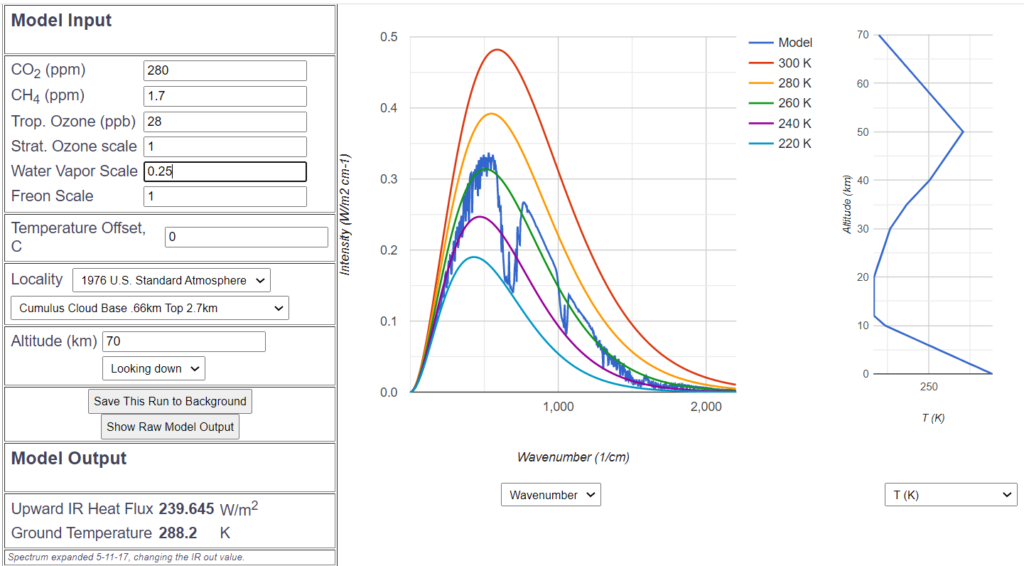
Das dunkelblaue Spektrum zeigt das bereits besprochene Verhalten. Das $CO_2$-Loch ist sehr ähnlich wie wir es schon kennen, der Einfluss des Wasserdampfes am rechten und am linken Rand ist ebenfalls gut erkennbar. Als Hilfslinien sind zusätzlich die Kurven eingetragen, die das ideale Strahlungsverhalten ohne Treibhausgase bei den Temperaturen 220° K bis 300° K kennzeichnen. Damit kann man die Abstrahltemperatur und damit die Energie an jeder Stelle des Spektrums schätzen.
Als nächsten Test wollen wir den heutigen $CO_2$-Gehalt von 415 ppm einstellen. Die Kurve von 1850 bleibt als blaue Referenz-Kurve im Hintergrund, und die rote Kurve von heute wird „darüber“ gezeichnet.
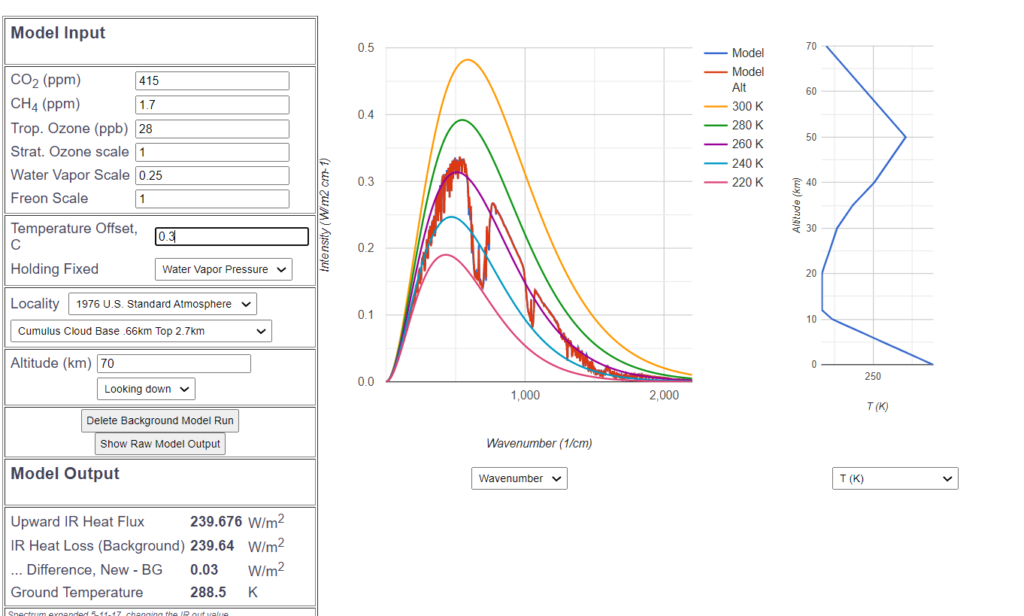
Was als erstes auffällt, ist, dass die Kurven fast identisch sind, und mit bloßem Auge nicht zu unterscheiden. Die rote Kurve verdeckt die blaue fast vollständig. Nur in den berechneten Werte links sieht man einen leichten Unterschied. Die um etwa 1 $\frac{W}{m^2}$ geringere Abstrahlung wird durch eine Temperaturerhöhung der Erdoberfläche von 0.3° kompensiert. Diese durchschnittlich 0.3° sind der effektive Treibhauseffekt seit Beginn der Industrialisierung bis heute, aufgrund des weithin akzeptierten MODTRAN Modells.
Wie ist es nun, wenn wir eine Verdoppelung des $CO_2$ Gehaltes von 280 ppm auf 560 ppm annehmen? Wiederum wird die neue Kurve der ursprünglichen blauen Kurve überlagert.
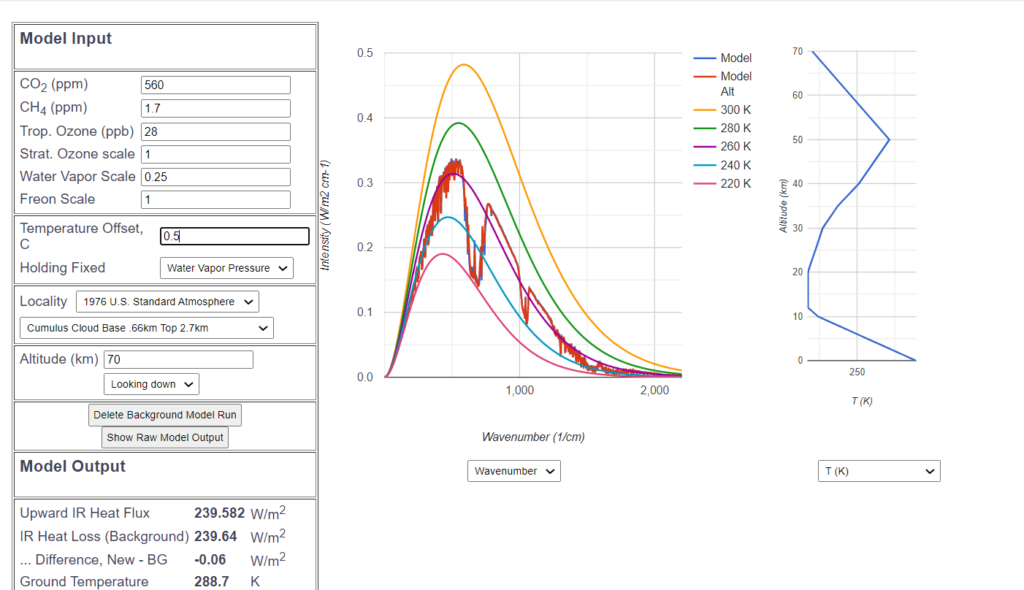
Und wiederum sind mit bloßem Auge kaum Unterschiede zu erkennen – einige kleine blaue Spitzen schauen bei der Wellenzahl 500 heraus, und die „$CO_2$“-Wanne ist einen Hauch breiter geworden. Um die aufgrund dieses minimalen Treibhauseffektes verminderte Infrarot-Abstrahlung zu kompensieren, wird die Bodentemperatur um insgesamt 0.5° C erhöht. Damit beträgt die Klimasensitivität mit der vorgenommenen MODTRAN Simulation ziemlich genau ein halbes Grad. Ein mögliches Erklärungsmodell für diese gemessene Sensitivität wird in diesem Artikel beschrieben.
Demnach besteht keinerlei Grund zu irgendeinem Alarmismus. Dieser Wert ist weit unterhalb der niedrigsten Annahmen des Weltklimarates.
Warum kommt der Weltklimarat zu anderen Ergebnissen
Die natürliche Frage nach diesen Überlegungen ist, warum der Weltklimarat, in dem ja die besten Klimaforscher vertreten sind, zu so viel pessimistischeren Ergebnissen kommen?
Ein zentrales Problem dabei ist, dass deren Klimamodelle extrem komplex sind und den Anspruch haben, die gesamte Komplexität des Klimageschehens abzubilden. Es gibt gute Gründe anzunehmen, dass dies unter den heutigen Voraussetzungen grundsätzlich nicht möglich ist, z.B. weil turbulente energiereiche Phänomene wie Meeresströmungen oder Tropenstürme in diesen Modellen nicht angemessen abbildbar sind. Ähnliche Modelle werden zur Wettervorhersage verwendet, und diese versagen bekanntlich bereits häufig bei Vorhersagen, die über wenige Tage hinausgehen.
Ein wichtiger Grund, die Gültigkeit der „globalen Zirkulationsmodelle“, kurz GCM genannt, anzuzweifeln, ist der, dass sie in zurückliegenden Vorhersagen für vergangene Klimadaten zu hohe Werte vorhergesagt haben.
Links die durchschnittliche Temperaturentwicklung (roter Balken) 1993-2012 – 0.15°/10 Jahre, rechts dasselbe im Zeitraum 1998-2012 – 0.03°/10 Jahre, und dazu die Ergebnisse von 110 verschiedenen Klimamodellen. Fast alle hatten deutlich höhere Temperaturen geschätzt.
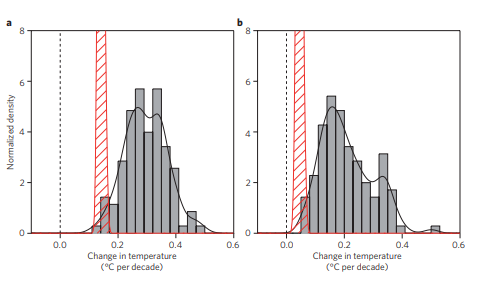
Simulation der IPCC-Annahmen
Mit dem MODTRAN Simulationsprogramm kann man aufgrund der von IPCC-nahen Autoren publizierten Daten allerdings deren Denkweise nachvollziehen. Dazu wird zunächst eine Atmosphäre ganz ohne Wasserdampf und ohne die anderen Treibhausgase angenommen, und dort die $CO_2$ Sensitivität gemessen.
Mit der MODTRAN Simulation wird diese Situation erreicht, wenn in der Standard-Atmosphäre alles bis auf den $CO_2$ Gehalt auf 0 gesetzt wird, also auch keine Wolken, kein Wasserdampf.
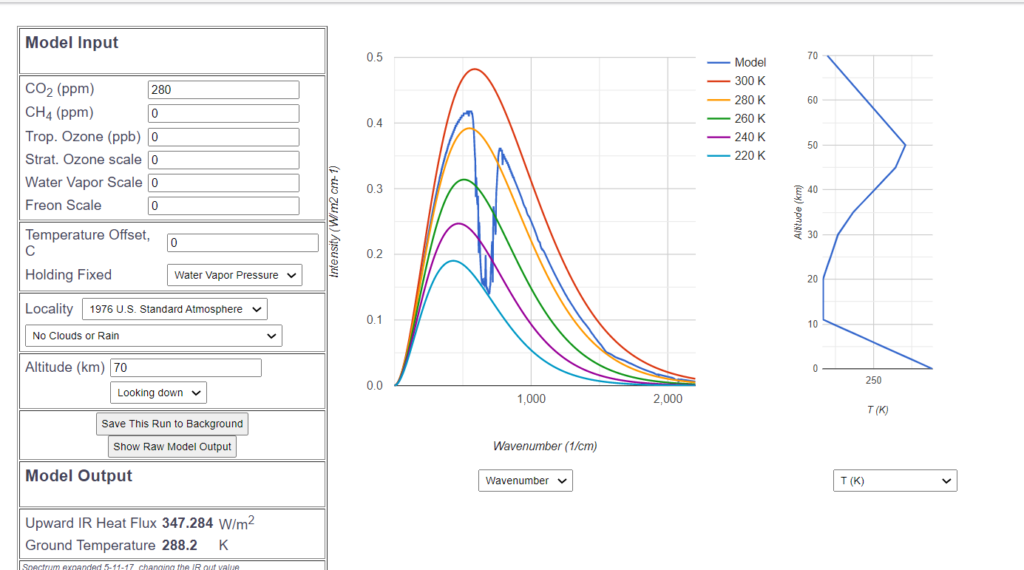
Damit steigt natürlich die hypothetische Abstrahlung auf einen unrealistisch hohen Wert von 347 $\frac{W}{m^2}$. Deutlich ist als einzige Abweichung von der „Idealkurve“ das bekannte $CO_2$-Loch zu erkennen.
Bei Verdoppelung des $CO_2$-Gehalts und gleichbleibender Bodentemperatur sinkt aufgrund des Treibhauseffekts jetzt die Abstrahlung um 3.77 $\frac{W}{m^2}$.
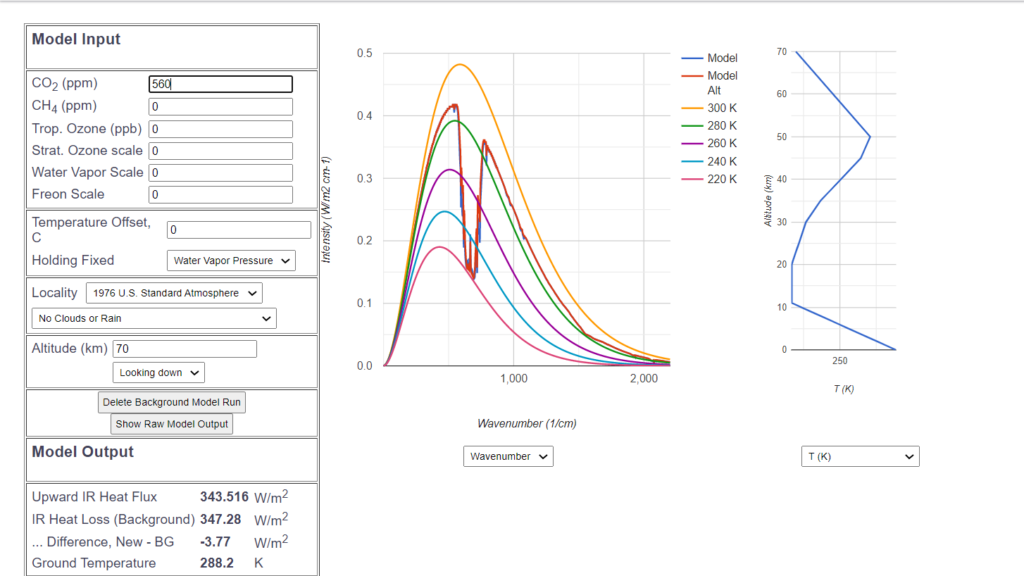
Das ist ziemlich genau der vom Weltklimarat veröffentlichte Wert des $CO_2$ bedingten „Strahlungsantriebs“ („radiative forcings“). Die verminderte Abstrahlung wird durch Temperaturerhöhung kompensiert:
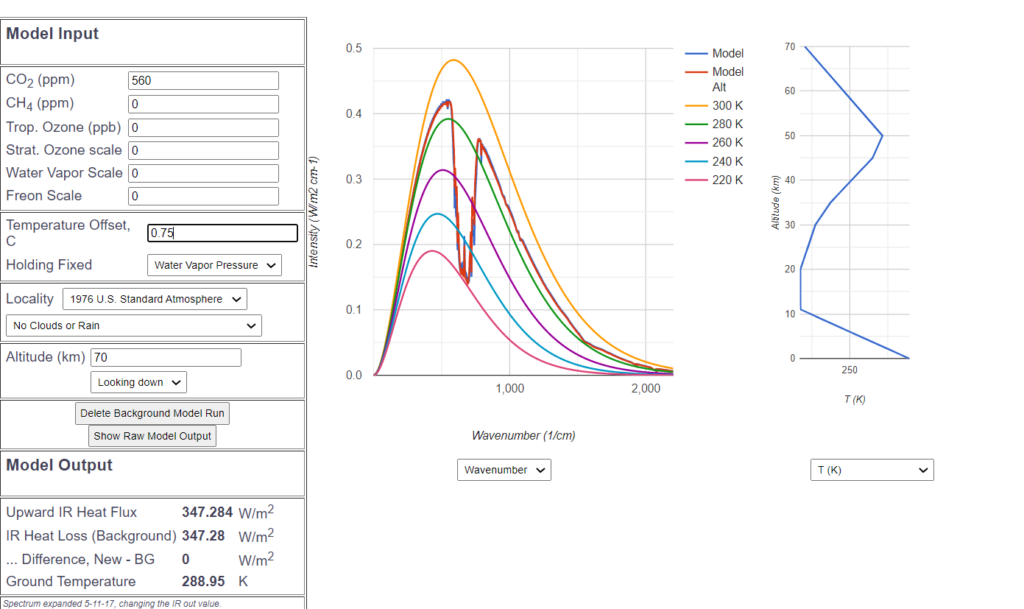
Demnach gleicht eine Temperaturerhöhung von 0.75° die Verdoppelung von $CO_2$ wieder aus, das wäre laut MODTRAN die Sensitivität. Viele Wissenschaftler kommen allerdings auf eine noch höhere Sensitivität von etwa 1°.
Diese Sensitivität wird aber — in gewisser Weise zu Recht — von den IPCC nahen Wissenschaftlern als die „reine $CO_2$-Sensitivität“ bezeichnet, weil dabei noch nicht der Einfluss des Wasserdampfes berücksichtigt ist. Da aber Wasserdampf ein noch stärkeres Treibhausgas ist, und durch die $CO_2$-bedingte Temperatur-Erhöhung mehr Wasserdampf erzeugt wird, wird in dieser Denkweise die $CO_2$ Sensitivität dadurch effektiv verdoppelt. So ist es möglich, zu einer Sensitivität von 2° zu kommen, die man dann durch andere Katastrophen-Szenarien wie das hypothetische Abschmelzen des Polareises noch willkürlich steigern kann. Völlig unberücksichtigt lassen sie dabei die Cumulus-Wolkenbildung, die ebenfalls durch Vergrößerung des Wasserdampfgehaltes verstärkt würde und die zur Reduzierung der einfallenden Energie führen würde, also zu einer starken negativen Rückkopplung. Allenfalls wird das Thema Wolken dadurch genutzt, indem argumentiert wird, dass die sehr hohen Zirrus-Wolken u.U. zu einer Verstärkung des Treibhauseffektes führen.
Nach meiner Auffassung ist aber das Auseinanderreißen von $CO_2$, Wolken und Wasserdampf bei der Berechnung der $CO_2$ Sensitivität nicht berechtigt. Werden alle Faktoren simultan berücksichtigt, führt das zu der oben genannten geringen Sensitivitität von 0.5°.