Versagen die CO2-Senken — oder deren Modelle?
[latexpage]
Einleitung – das Modell-Dilemma
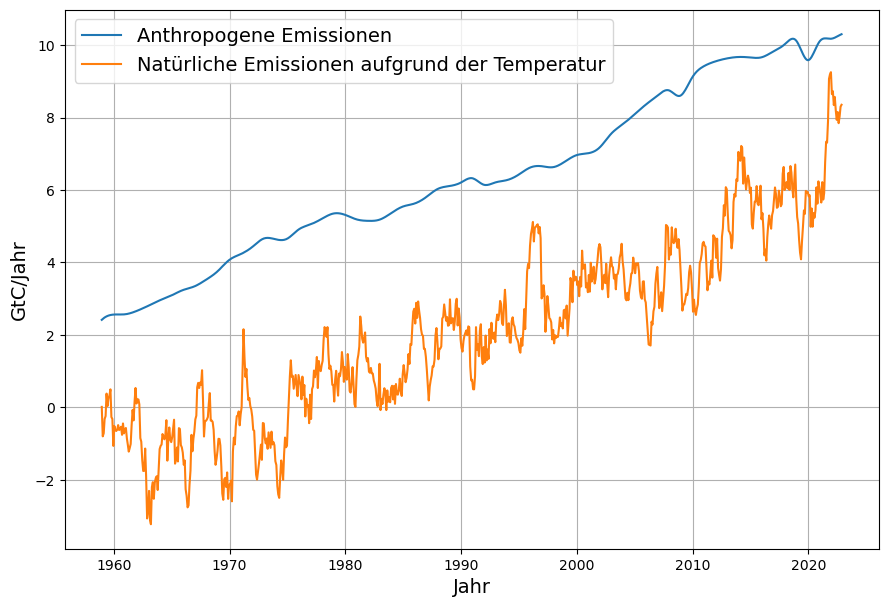
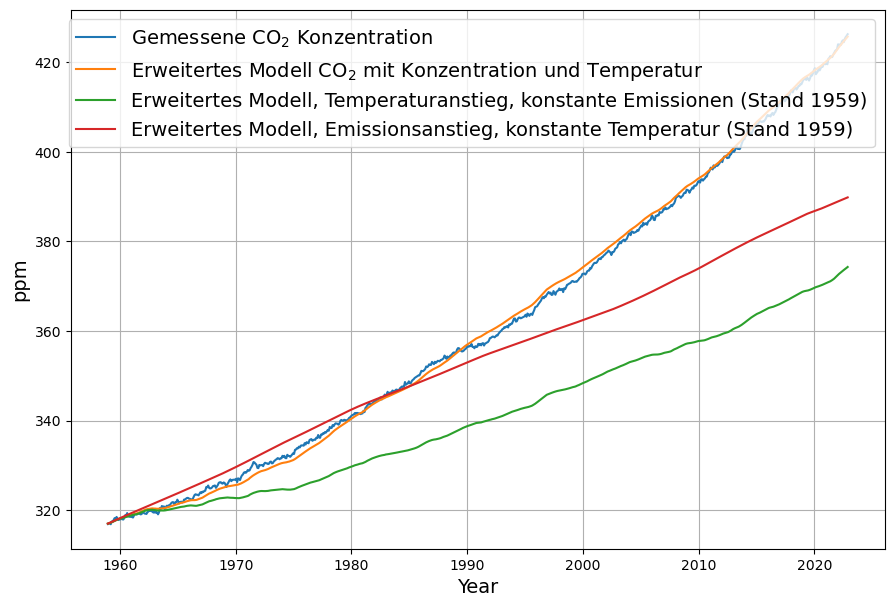
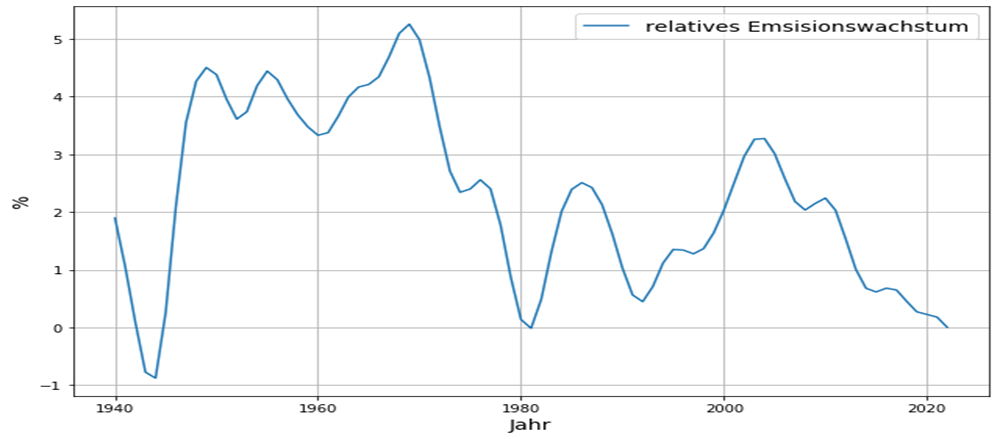
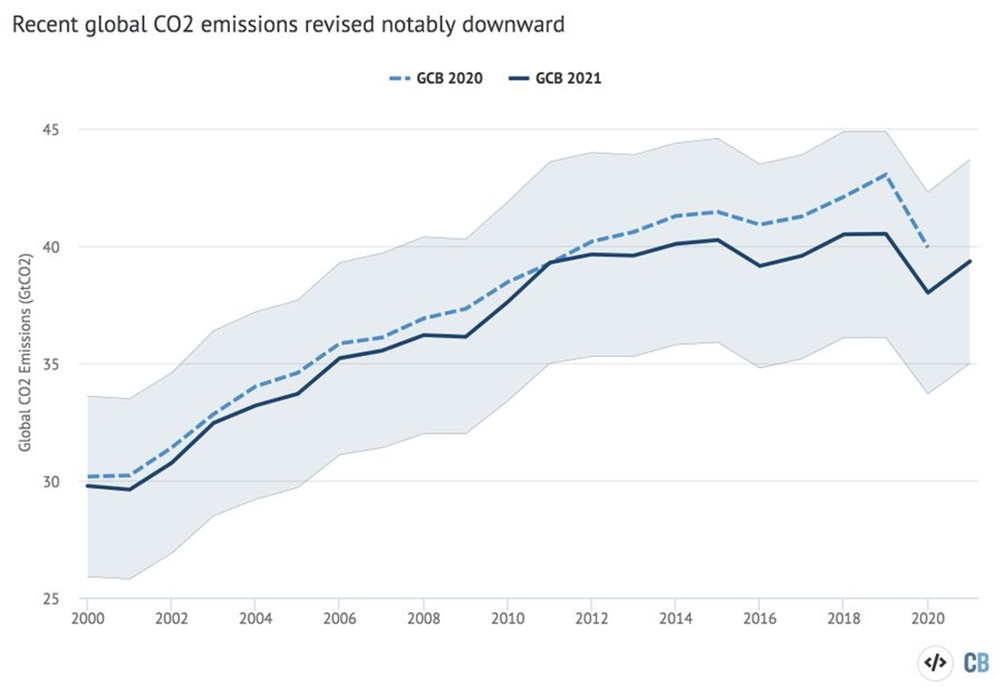
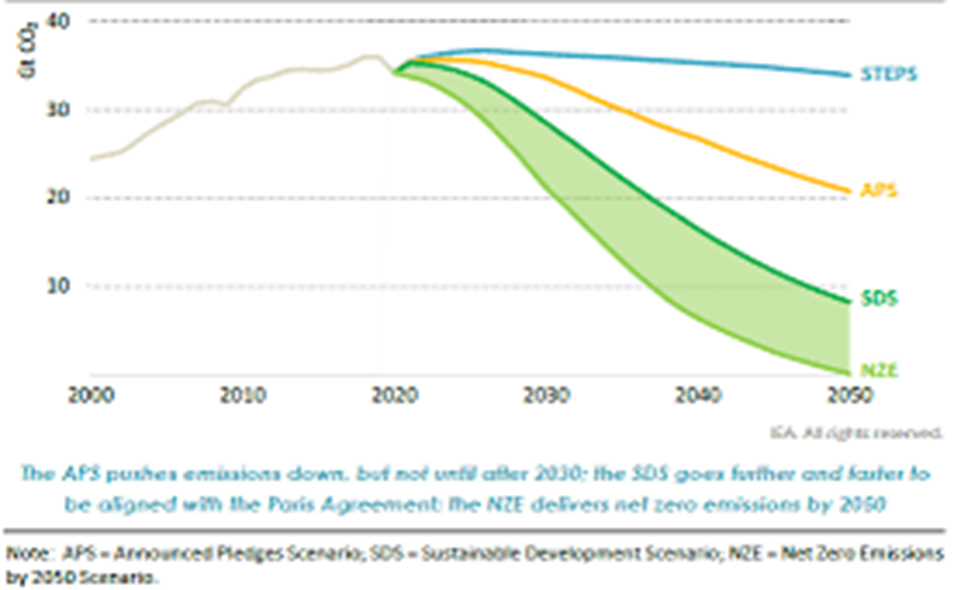
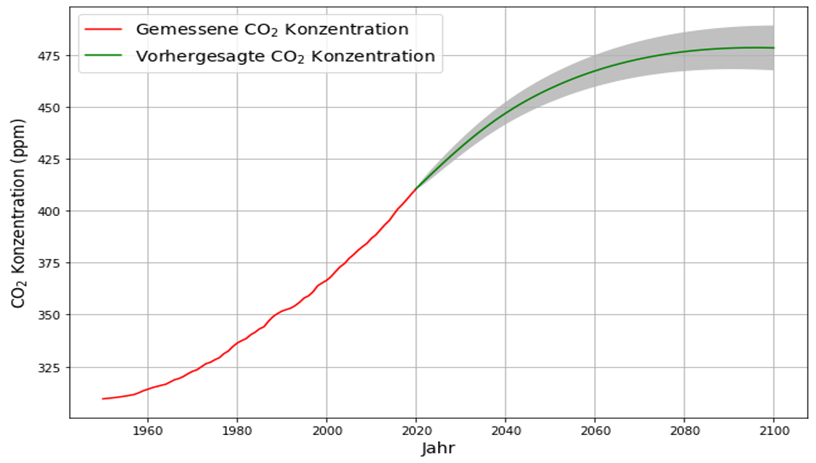
Es besteht weithin Konsens darüber, dass die seit 1850 angestiegenen CO2-Konzentration in der Atmosphäre von den seither stark angewachsenen anthropogenen CO2-Emissionen herrührt. Seit rund 10 Jahren sind die anthropogenen Emissionen im Rahmen der Messgenauigkeit konstant, und im weiteren Verlauf ist keine größere Abweichung von diesem Trend zu erwarten. Zum Zweck der Veranschaulichung werden für das Zukunftsszenario konstante Emissionen angenommen, in Anlehnung an das Stated Policy Szenario der IEA. Diese bestreitbare Annahme ist für die eigentliche Rechnung irrelevant, da diese ausschließlich mit Messungen vergangener Daten erfolgt. Die gemessenen Emissionen und das angenommene künftige Emissionsszenario wird in Abb. 1 gezeigt. Die Verwendung der etwas ungewöhnlichen Maßeinheit ppm für Emissionen ist der Notwendigkeit des Vergleichs von Emissionen und Konzentration geschuldet ((1 ppm = 2,123 Gt C = 7,8 Gt CO2).
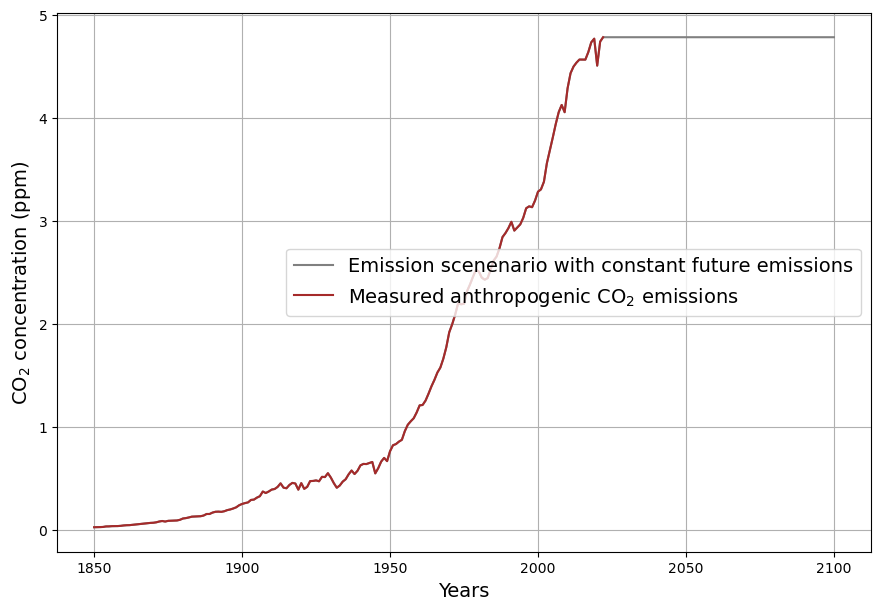
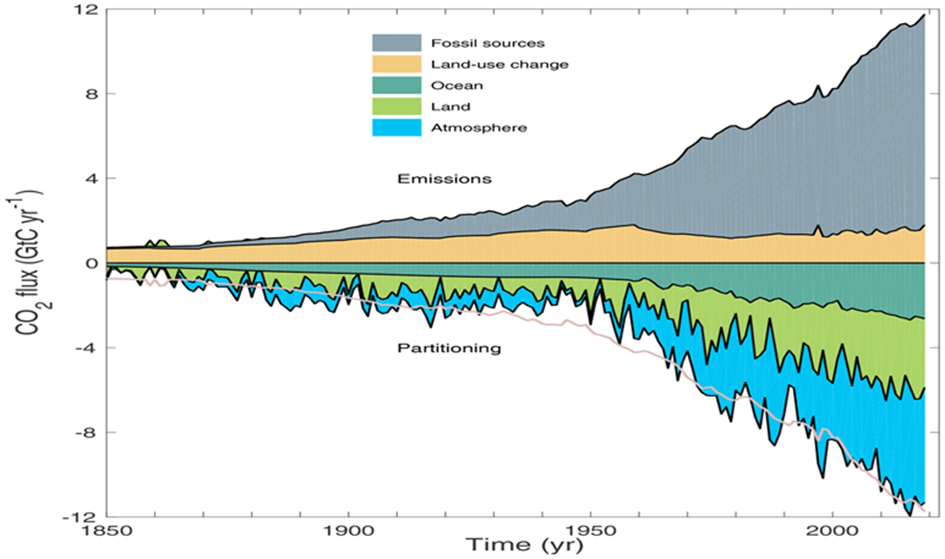
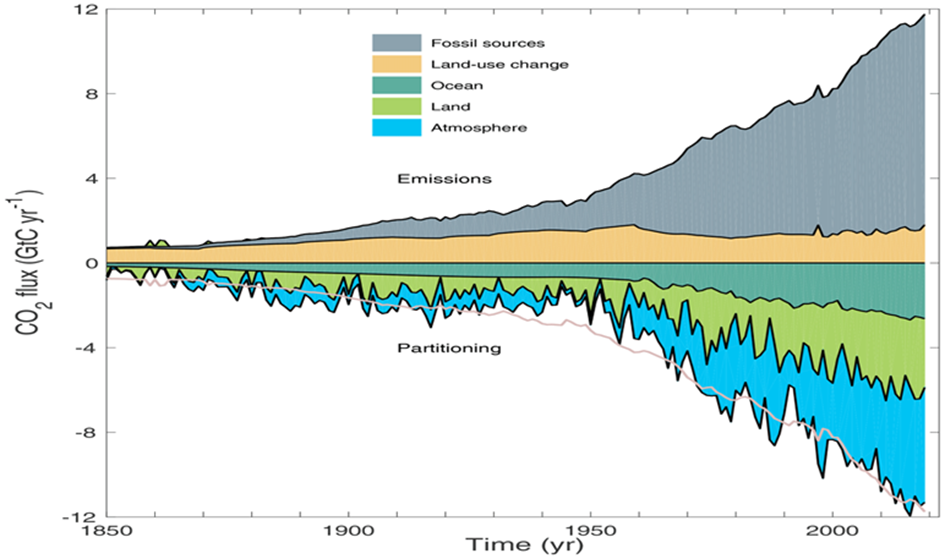
Die anthropogenen Emissionen verbleiben nicht vollständig in der Atmosphäre. Deren Konzentration wächst bislang ungefähr nur halb so stark an, als wenn alle anthropogenen Emissionen in der Atmosphäre blieben, wie in Abb. 2 dargestellt. Dieser Zusammenhang gilt seit etwa 1950, als die Phase des stärkstens Emissionswachstums von etwa 4% pro Jahr begann, die bis in Mitte der 70-er Jahre anhielt.
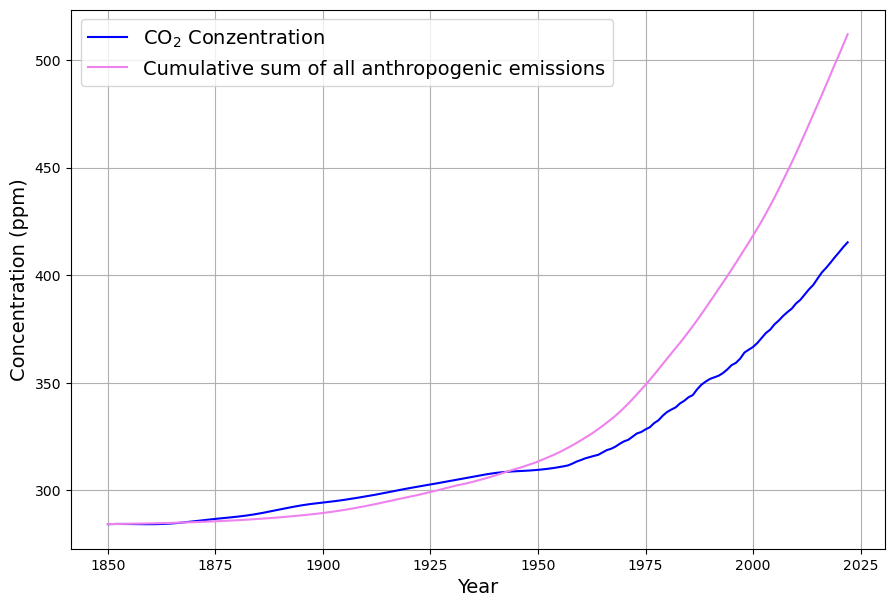
Der etwas merkwürdige Umstand, dass zwischen 1875 und 1945 die tatsächliche Konzentration größer ist als die hypothetische Konzentration, bei der alle anthropogenen Emissionen in der Atmosphäre bleiben, ist wahrscheinlich darauf zurückzuführen, dass die in der ersten Hälfte des 20. Jahrhunderts signifikant großen Emissionen aufgrund von Landnutzungsänderungen hier nicht berücksichtigt wurden. Auch dies spielt für die hier vorgenommenen Rechnung nur sehr bedingt eine Rolle, weil für die Berechnung des Ergebnisses nur Daten nach 1960 verwendet werden.
Das verminderte Ansteigen der Konzentration im Vergleich zu den anthropogenen Emissionen hat seine Ursache in den beiden großen Senkensystemen, den Landpflanzen und den Weltmeeren, die beide beträchtliche Mengen an CO2 absorbieren. Die wichtige Frage ist, wovon diese Absorption abhängt, und noch wichtiger ist, wie sich die Stärke der Absorption weiterentwickelt. Dies wird reflektiert in den verschiedenen Senkenmodellen. Von den vielen Spielarten dieser Modelle werden hier zwei wichtige, prinzipiell verschiedene Repräsentanten untersucht:
- das lineare Senkenmodell, bei dem die Senkenwirkung eine strikt lineare Funktion der CO2-Konzentration ist,
- das Berner Modell, das davon ausgeht, dass etwa 20% der Emissionen für sehr lange Zeit in der Atmosphäre verbleiben.
Welches der Modelle richtig ist, hat schwerwiegende Auswirkungen auf den Umgang mit CO2. Wenn ein Teil davon quasi für immer in der Atmosphäre bleibt, impliziert das letzten Endes die Notwendigkeit der Reduktion der anthropogenen Emissionen auf 0, also eine Budgetierung, was in Deutschland und der EU aktuell politische Zielvorstellung ist. Wäre hingegen das lineare Modell korrekt, könnten wir uns darauf verlassen, dass mit steigender Konzentration auch entsprechend mehr CO2 absorbiert wird und das Pariser Klimaziel, das Gleichgewicht von CO2 Quellen und Senken auch bei kaum verändertem Emissionsverhalten in der 2. Hälfte dieses Jahrhunderts erreicht wird.
Deswegen beschäftigt sich dieser Beitrag damit, ein Kriterium zu finden, um mit existierenden Messdaten die Korrektheit des einen oder anderen Modells zu belegen.
Was sind Senken? Eine formale Beschreibung
Zunächst wird die messbare Senkenwirkung $S_i$ des Jahres $i$ als Bilanzgleichung als Folge der Erhaltung der Gesamtmasse des CO2 mit der Kontinuitätsgleichung bestimmt. Der Konzentrationszuwachs $G_i$ der Atmosphäre ergibt sich als Differenz aller Emissionen, also der anthropogenen Emissionen $E_i$ sowie der natürlichen Emissionen $N_i$, und der gesamten Absorptionen $A_i$ (anschaulich wie sich der (Jahres-)Gewinn aus Einnahmen und Ausgaben bei einem Konto ergibt):
$G_i= C_i – C_{i-1} = E_i + N_i – A_i$ (Gleichung 1)
Die globale Senkenwirkung $S_i$ ist der Teil der anthropogenen Emissionen $E_i$, die nicht zum Anwachsen der Konzentration $G_i$ beitragen:
$S_i = E_i – G_i$ (Gleichung 2)
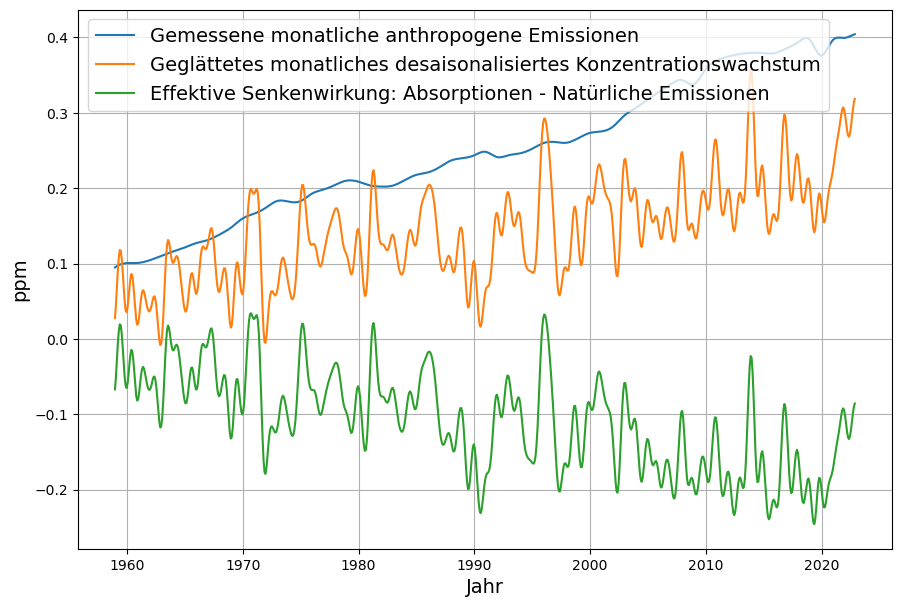
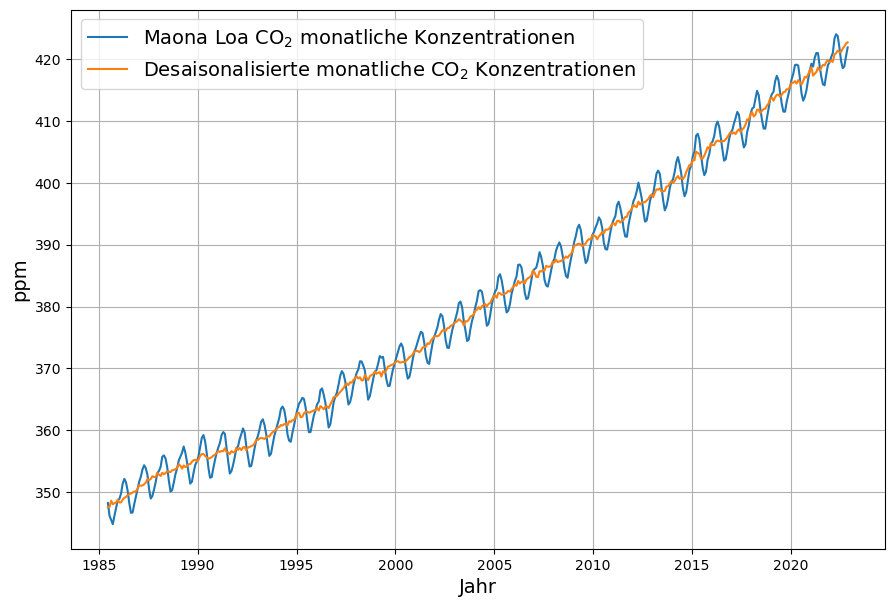
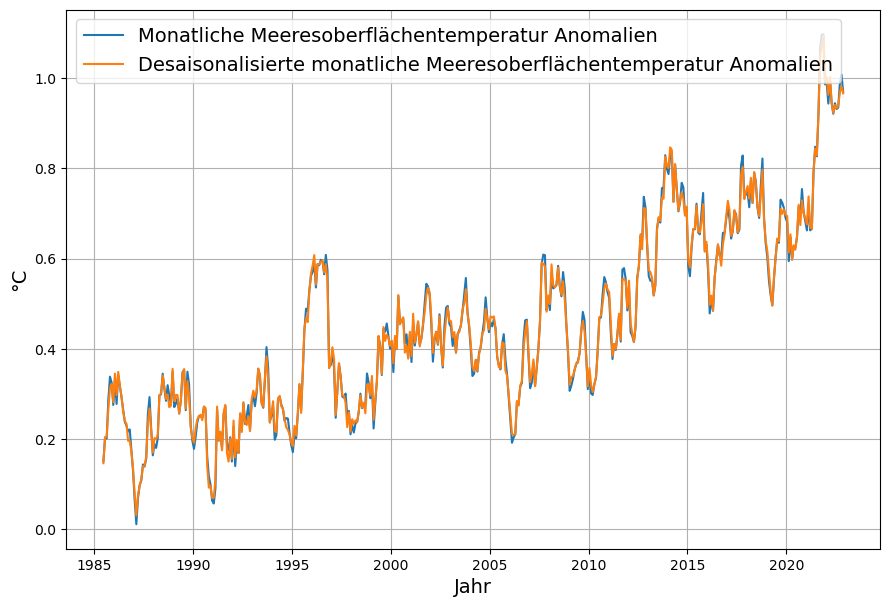
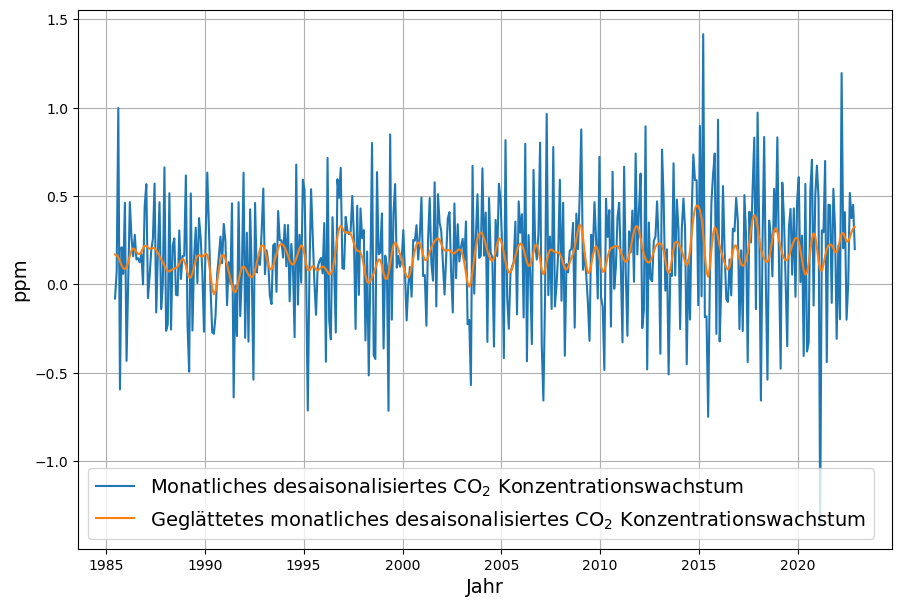
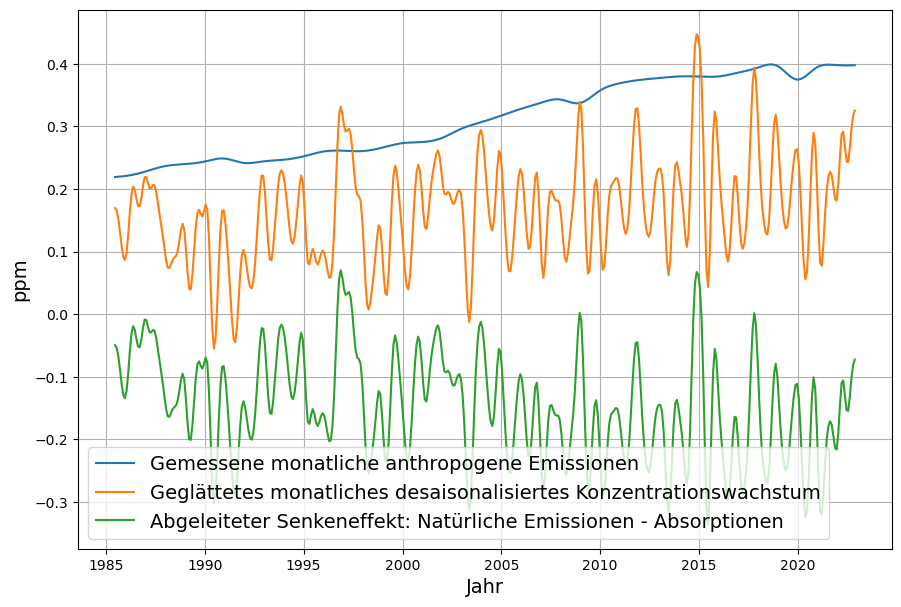
Diese Senkenwirkung ist aus den verfügbaren Emissions- und CO2-Konzentrations-Daten (monatliche Konzentrationsdaten von Mauna Loa) ohne Modellierung berechenbar und ist in Abbildung 3 als Zeitserie ab 1960 gezeigt. Die Daten des monatlich gemessenen Konzentrationszuwachses sind desaisonalisiert, indem jeweils die Differenz zum gleichen Vorjahresmonat bestimmt wird. Emissionen und Konzentration sind in der gleichen Maßeinheit ppm gemessen (1 ppm = 2,123 Gt C = 7,8 Gt CO2)
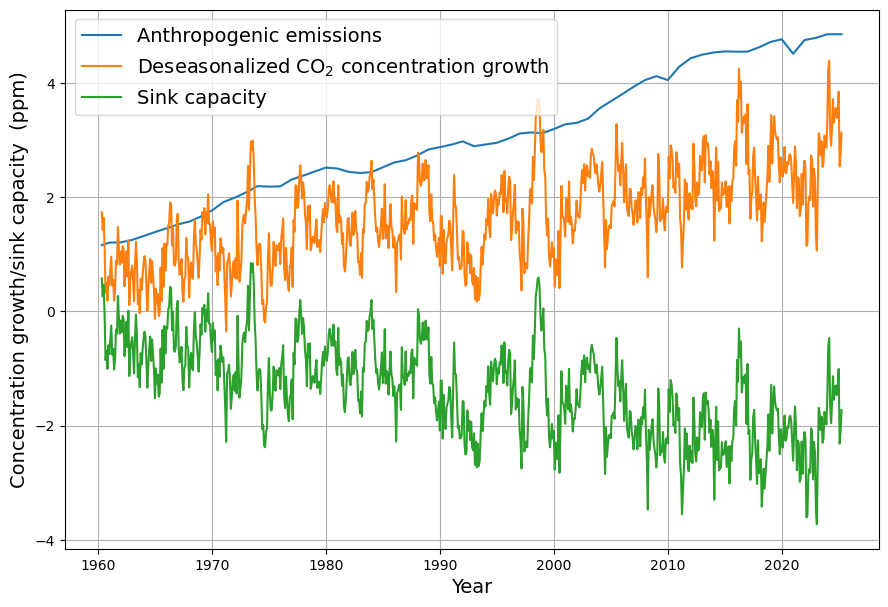
Demzufolge ist die Senkenwirkung auch die Differenz zwischen Absorptionen $A_i$ und natürlichen Emissionen $N_i$
$S_i = A_i -N_i $ (Gleichung 3)
Daraus folgt auch, dass die — mit großen Unsicherheiten behafteten — Emissionen durch Landnutzungsänderungen als zu den unbekannten natürlichen Emissionen gehörig gerechnet werden.
Die so definierte globale Senkenwirkung ist also einer einfachen Messung zugänglich. Daher wird eine Methode gesucht, um mit dieser gemessenen Senkenwirkung das jeweilige Senkenmodell zu bewerten. Ziel dieser Untersuchung ist nicht, die Korrektheit der jeweiligen Modelle aufgrund deren jeweils angenommenen kausalen Mechanismen zu bewerten, sondern einzig und allein, ein mathematisch statistisches Kriterium zu finden, um aufgrund von Messdaten zu entscheiden, welches Modell besser mit der Realität übereinstimmt1.
Die beiden Senkenmodelle
Das lineare Senkenmodell
Es werden 2 Senkenmodelle gegenübergestellt. Das eine, das „lineare Senkenmodell“ oder auch „Badewannenmodell“ geht davon aus, dass die Senkenwirkung im Jahre $i$, $S_i$ streng linear mit der CO₂-Konzentration (des Vorjahrs) $C_{i-1}$ anwächst (eine genauere Analyse ergibt, dass der Erwartungswert der Zeitdifferenz zwischen Konzentration und Senkenwirkung etwa 15-18 Monate beträgt):
$S_i = a\cdot C_{i-1} + b = a\cdot(C_{i-1} – C^0)$ (Gleichung 4)
wobei $C^0=-b/a$ die angenommene präindustrielle Gleichgewichtskonzentration ohne anthropogene Emissionen darstellt.
Aus den Daten des Zeitraums 1960-2025 ergeben sich diese Schätzwerte:
$a=0,0174, b=-4,87, C^0 =280 $ ppm
Der Schätzwert der Gleichgewichtskonzentration $C^0$ stimmt bemerkenswert gut mit der gewöhnlich angenommenen präindustriellen Konzentration von 280 ppm überein.
Bei der Modellgleichung handelt es sich um eine diskretisierte Version einer Differenzialgleichung 1. Ordnung mit der Impulsantwort (IRF=“impulse response function“)
$IRF^{linear}(t)=e^{-\frac{t}{\tau}}$
mit $\tau=1/a\approx 57 $ Jahre.
Entscheidend ist, dass die Impulsantwort des linearen Systems vollständig auf 0 abklingt, was bedeutet, dass das atmosphärische CO₂ mit der Zeit vollständig von den Senken absorbiert wird.
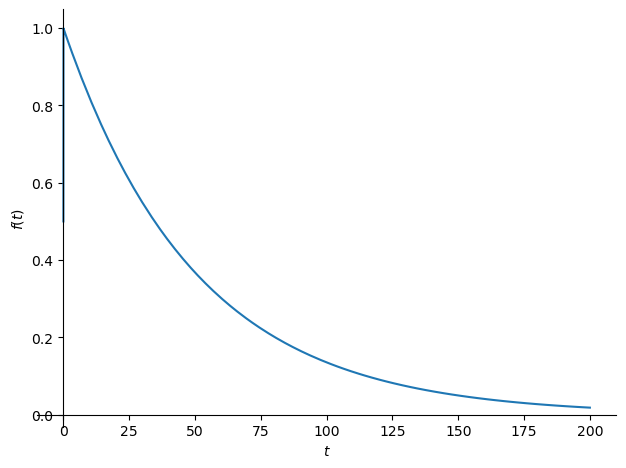
Das Berner Modell
Um nicht voreilig falsche Schlussfolgerungen aus dem Berner Modell zu ziehen, erscheint es wichtig, zunächst einen Vorläufer des Berner Modells zu betrachten, das sogenannte 2-Boxen-Modell. Ausgangspunkt des 2-Boxen-Modells ist die im Prinzip richtige Überlegung, dass auch die CO₂-Senken, die Ozeane und die Landpflanzen, endlich sind und nur eine begrenzte Menge an CO₂ aufnehmen können. Das einfachste Modell, das diesen Umstand berücksichtigt, ist das 2-Boxen-Modell gemäß Abb. 5, wonach die Atmosphäre die eine Box darstellt, die Ozeane zusammen mit den Landpflanzen die 2. Box.
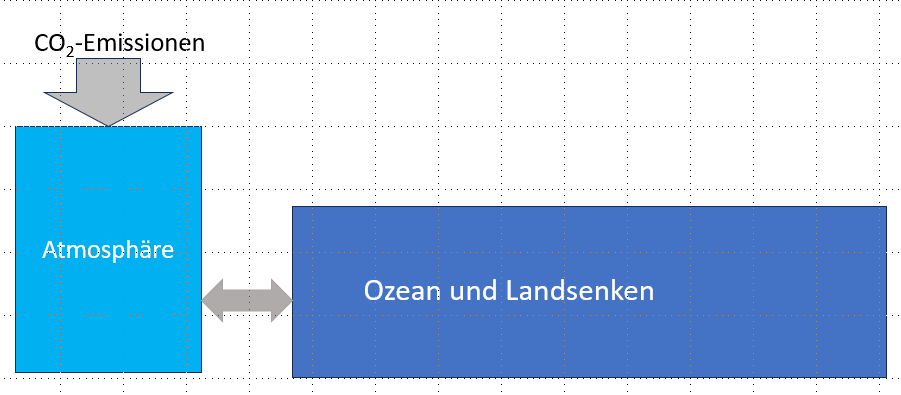
Diese 2. Box ist um den Faktor $k$ größer als die erste Box. Um den Effekt zu verdeutlichen, wird $k=3$ angenommen. Es erscheint extrem, dass die Ozeane und die Landpflanzen zusammen nur 3-mal größer angenommen werden als die Atmosphäre. Aber das ist tatsächlich der Wert, von dem die aktuelle Klimaforschung (z.B. Prof. Marotzke bei Markus Lanz, 10. Juli 2025, Minute 21:30) ausgeht, obwohl bekannt ist, dass alleine die Ozeane insgesamt etwa 50-mal so viel CO₂ gebunden haben wie die Atmosphäre. Beim Berner Modell ist der Faktor $k$ eher bei 4. Wenn man sich vorstellt, dass der aufnehmende Container tatsächlich nur 3-mal größer ist als die Atmosphäre, dann ist auch klar, dass von jedem zusätzlichen CO₂-Eintrag in die Atmosphäre am Ende, d.h. im Gleichgewichtszustand, 25% in der Atmosphäre zurückbleiben, und nur 75% von den Senken aufgenommen werden können. Dies wird mit der Impulsantwort des 2-Boxen Modells in Abb. 6 verdeutlicht.
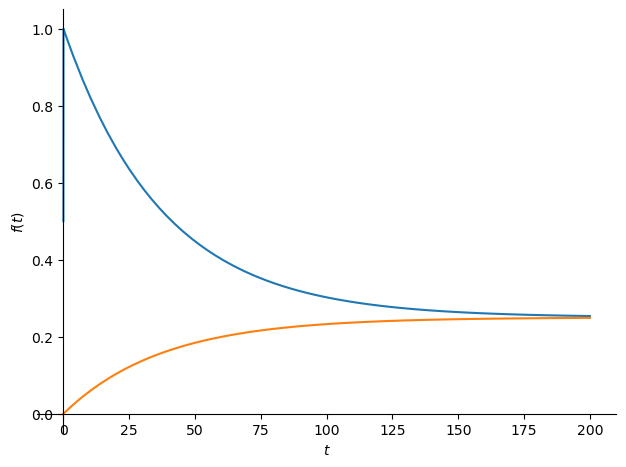
Das Berner Modell ist ein 4-Boxen-Modell, skizziert in Abb. 7. Es unterteilt den Ozean in 2 Teile. Während in dem oberen Teil der Gasaustausch mit einer ähnlichen Zeitkonstante wie beim linearen Modell geschieht (da dafür nur die oberste Schicht „Mixed Layer“ berücksichtigt wird, ist der Austausch noch schneller als beim linearen Modell) , geschieht der Fluss in die Tiefsee durch eine sehr langsame Diffusion. Die 4. Box repräsentiert die Landpflanzen. Dadurch, dass die Tiefsee durch den langsamen Diffusionsprozess für Hunderte von Jahren „abgeschirmt“ ist, erklärt sich die vermeintlich kleine „Ozean-Box“ und der daher große konstante Rest von über 20% in der Atmosphäre.
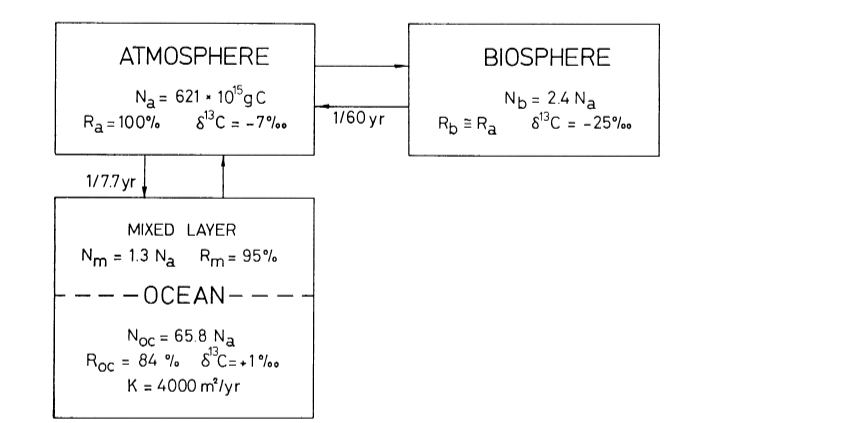
Die publizierte Näherungsgleichung des Bern-Modells ist
$ IRF^{Bern}(t) =a_0 + \sum_{i=1}^3 a_i\cdot e^{-\frac{t}{\tau_i}}$ (Gleichung 5)
mit
$a_0=0.21787, a_1=0.22896, a_2=0.28454, a_3=0.26863$,
$\tau_1=381.33, \tau_2=34.785, \tau_3=4.1237$.
Die mathematische Form der Näherungslösung und die zitierte Publikation suggerieren, dass es sich um 4 parallele Prozesse handelt. Das ist aber nicht so, es ist nur eine Näherungslösung eines komplexen 4-Boxen-Prozesses, um damit den Prozess einfacher als gewichtete Summe linearer Prozesse formulieren zu können.
Abb. 6 zeigt die Impulsantworten (IRF) des Bern-Modells (orange) im Vergleich zum obigen linearen Modell (grün) und zum 2-Boxen-Modell (magenta).
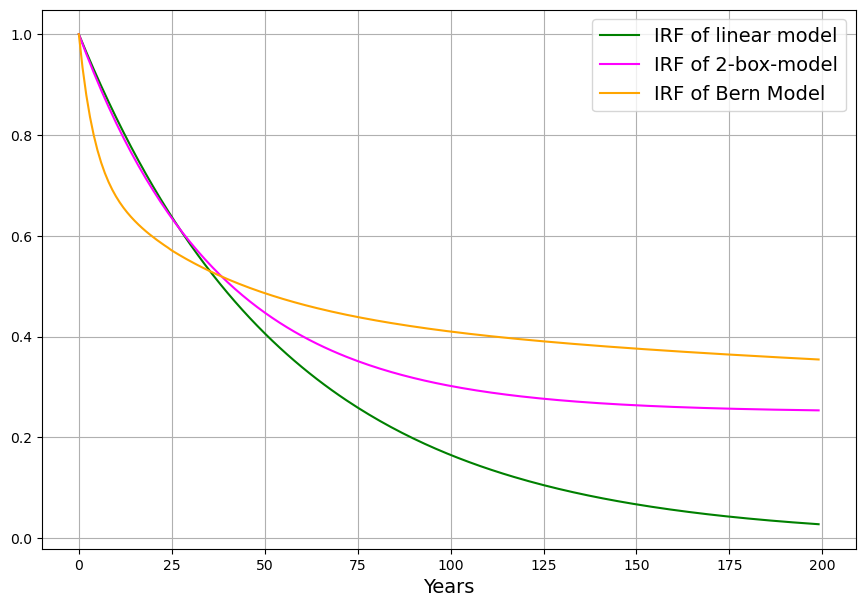
Während zu Beginn der Konzentrationsabfall des Berner Modells stärker ist als beim linearen Modell, wird der Verlauf bald flacher, sodass nach 100 Jahren nur 60% absorbiert sind, beim linearen Modell sind es da bereits 85%. Das 2-Boxen-Modell liegt vom Verlauf her zwischen dem linearen und dem Berner Modell, langfristig geht es ähnlich wie das Berner Modell in die Sättigung, d.h. es bleibt ein substantieller Teil des CO₂ in der Atmosphäre.
Anwendung auf den realen Emissionsverlauf
Der entscheidende Test erfolgt mit den echten gemessenen Daten, den gemessenen anthropogenen Emissionen gemäß Abb. 1.
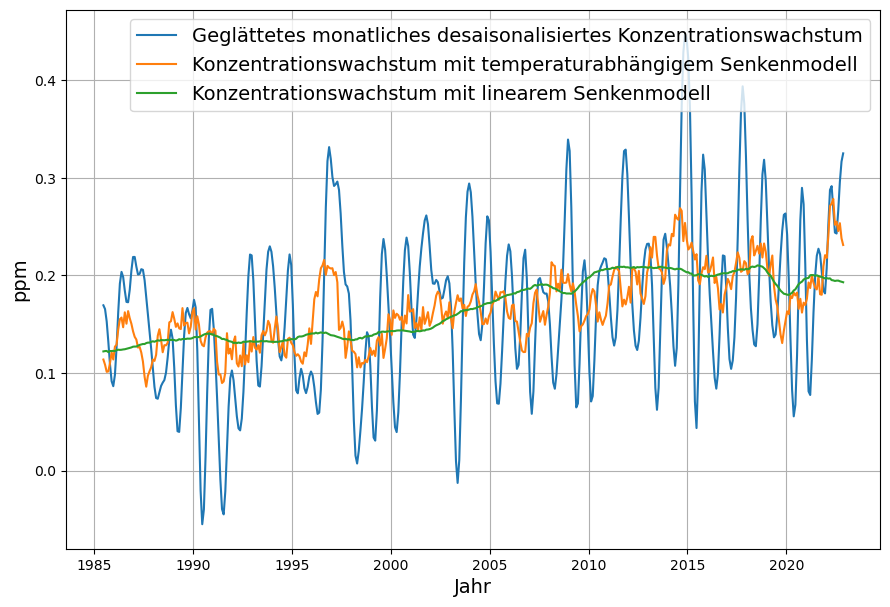
Durch Faltungen mit den beschriebenen jeweiligen Impulsantworten ergeben sich die Konzentrationsverläufe der beiden Modelle und einer natürlichen Gleichgewichtskonzentration von 285 ppm (Abb. 9). Mit den Zeitreihen bis Ende 2024 sind die Unterschiede der Modelle bei der Rekonstruktion der gemessenen CO2-Konzentration sehr gering (Da die Messdaten vor 1960 ohnehin unzuverlässig sind, sind die Abweichungen vor 1960 von untergeordnetem Interesse). Zwischen 1960 und 2020 stimmen nicht nur die beiden Modelle untereinander überein, sondern auch mit den gemessenen Konzentrationsdaten2.
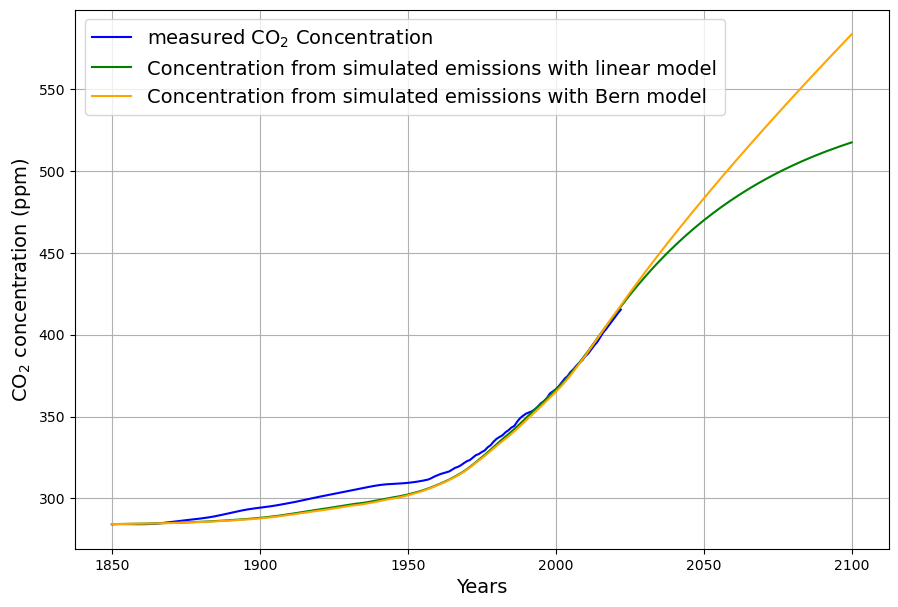
Es ist aus Abb. 9 aber deutlich erkennbar, dass die Senkenwirkung des Berner Modells im Vergleich zum linearen Modell auf lange Sicht deutlich nachlässt und als Folge davon die Konzentration ab 2030 stärker anwächst als beim linearen Modell. Beim direkten Vergleich der Konzentrationen liegt die Entscheidbarkeit, welches Modell die Wirklichkeit korrekt abbildet, leider in der Zukunft. Es wird ein empfindlicheres Kriterium benötigt. Deswegen wird für beide Modelle die Senkenwirkung als Vergleichskriterium berechnet, auf die gleiche Weise wie bei den realen Messdaten.
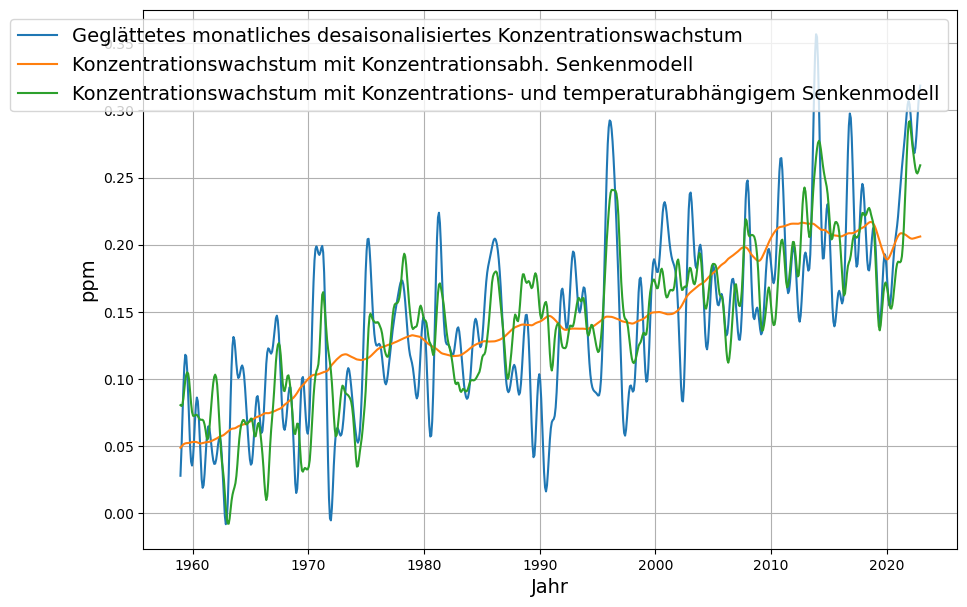
Durch Differenzbildung jeweils benachbarter Datenpunkte aus dem modellierten Konzentrationsverlauf wird das Konzentrationswachstum mit Gleichung (1) bestimmt. Die für das Unterscheidungskriterium wichtige gemessene Senkenwirkung wird aus der Differenz zwischen gemessenen Emissionen und dem so bestimmten Konzentrationswachstum nach Gleichung (2) bestimmt. Die daraus ermittelten jeweiligen Senkenwirkungen sind in Abbildung 10 zusammengefasst.
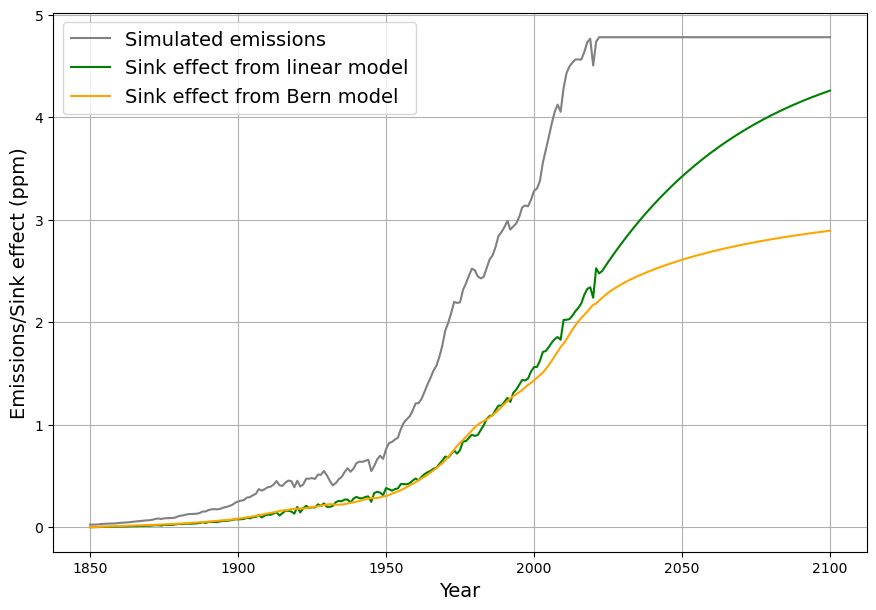
Wiederum zeigt sich, dass das lineare Modell und das Berner Modell sich bis 2020 nur sehr geringfügig unterscheiden. Allerdings werden die Unterschiede danach sehr groß, die Senkenwirkung des Berner Modells geht bis Ende des Jahrhundert nahezu in die Sättigung (aber nicht gegen 0), während die Senkenwirkung des linearen Modells sich den anthropogenen Emissionen im Sinne des Gleichgewichts von Senken und Quellen vom Pariser Klimaabkommens nähert.
Um schon heute eine Aussage zur Gültigkeit des jeweiligen Modells machen zu können, wird ein Kriterium benötigt, mit dem sich aus Daten der Vergangenheit bereits ein messbarer Unterschied der jeweiligen Senkenwirkung feststellen läßt.
Kriterium zur Unterscheidung des linearen Modells von den „abflachenden“ Modellen
Ausgehend von Gleichung (4), kann der relative Senkeneffekt bzw. das Senkenverhältnis eines beliebigen Senkenmodells zu jedem Zeitpunkt dadurch beschrieben werden, indem die Absorptionskonstante $a$ des linearen Modells zu einer zeitabhängigen Variablen $a_i$ modifiziert wird:
$S_i = a_i\cdot(C_{i-1} – C^0)$
Der Wert dieses zeitabhängigen Senkenverhältnisses $a_i$ ist definiert als Verhältnis der aus Emissionen und Konzentrationswachstum abgeleiteten Senkenwirkung $S_i$ und der über die präindustrielle Gleichgewichtskonzentration $C^0$ ppm hinausgehende Konzentration des Vorjahres3:
$a_i = \frac{S_i}{C_{i-1}-C^0} = \frac{E_i – (C_i – C_{i-1})}{C_{i-1}-C^0}$
Demzufolge ist das Senkenverhältnis $a_i$ eine Größe, die außer von der Konstanten $C^0$ nur von den gemessenen anthropogenen Emissionen und den modellierten oder gemessenen Konzentrationen $C_i$ abhängt.
In Abb. 11 wird das „Senkenverhältnis“ $a_i$ für das lineare Modell (grün) und das Bern-Modell (orange) dargestellt.
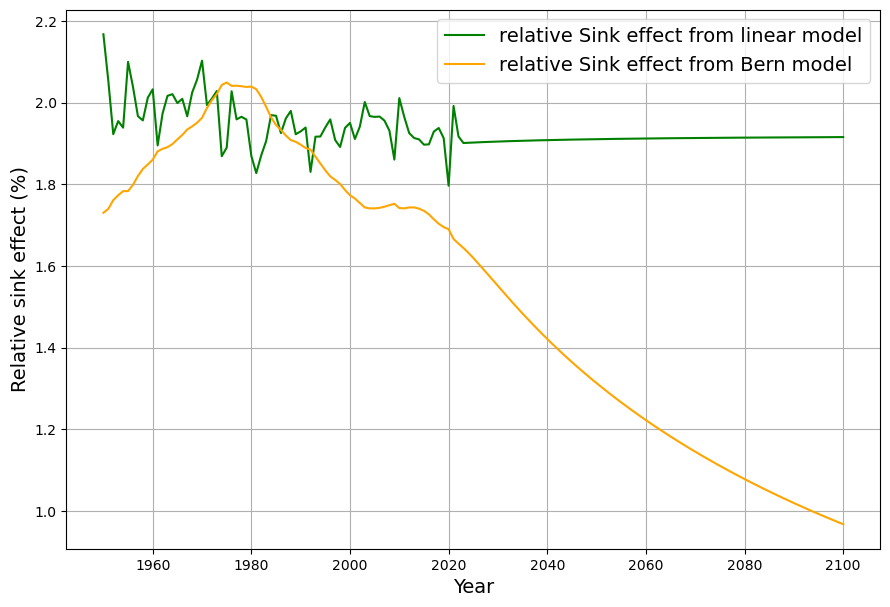
Nach einem leichten Anstieg des Senkenverhältnisses während der Phase exponentiellen Emissionswachstums bis 1975 ist beim Berner Modell ab 1980 ein deutlicher Abfall des Senkenverhältnisses erkennbar, währen das Senkenverhältnis beim linearen Modell erwartungsgemäß weitgehend konstant ist.
Um aus dieser graphischen Veranschaulichung mit Daten der Vergangenheit statistisch auswertbare Messdaten zu erhalten, wird der Verlauf der relativen Senkenwirkung im Zeitraum der 42 Jahre von 1980 bis 2022 jeweils mit einer Geraden approximiert (Abb. 12):
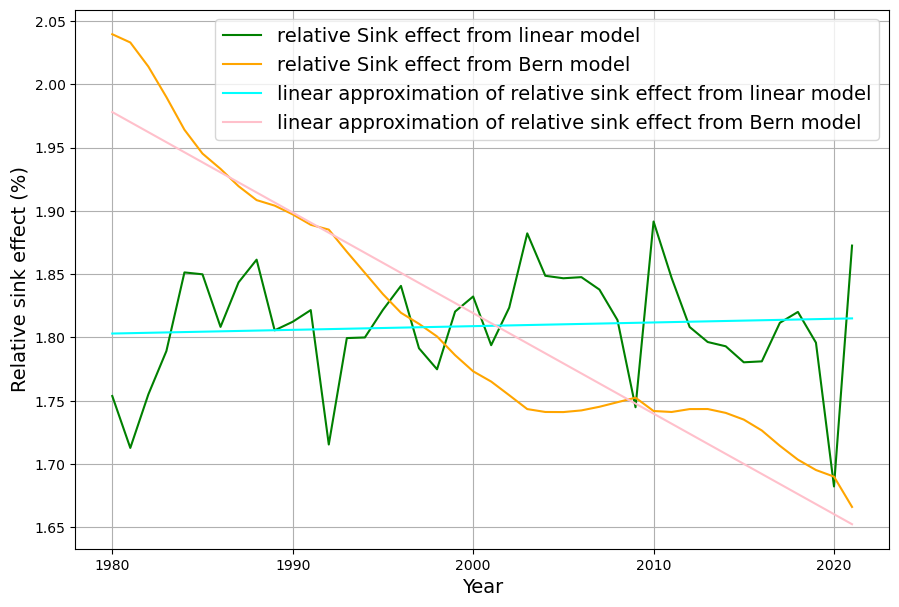
Der Trend der beiden Kurven wird durch die Steigung der Geraden gut wiedergegeben. Die Steigung dieser Geraden ist daher das gesuchte signifikante Unterscheidungskriterium der beiden Modelle. Aus der Kleinste-Quadrat Schätzung der Geradengleichung ergibt sich auch der Standard-Fehler der Steigung. Diese beiden Messwerte werden nun mit ihren Fehlerverteilungen in einem Diagramm (Abb 13) aufgetragen. Um ein dimensionsloses Ergebnis zu erhalten, wird der Quotient der Steigung und des Erwartungswertes am Mittelpunkt des Zeitraums aufgetragen und als relative Steigung (in %) als Wert auf der X-Achse von Abb. 13 verwendet. Das Diagramm zeigt die Wahrscheinlichkeitsverteilungen für die relative Steigung des Senkenverhältnisses beider Modelle.
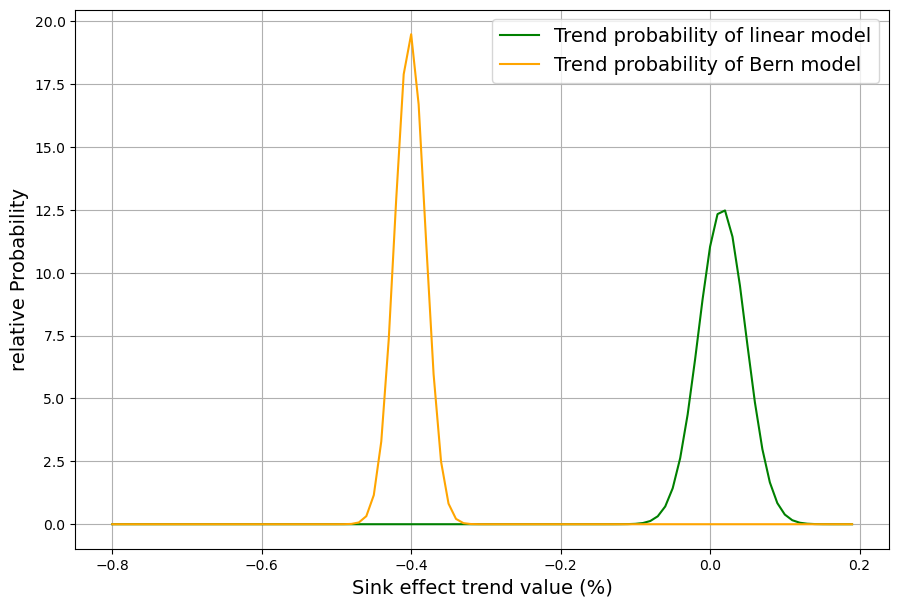
Die beiden Wahrscheinlichkeitsverteilungen sind so deutlich disjunkt, dass damit ein Kriterium gefunden ist, in dem sich die beiden Modelle sehr stark unterscheiden, und zwar bereits während des Zeitraums der letzten 40 Jahre. Im Klartext heißt das, dass es kaum Trendabweichungen des Senkenverhältnisses von 0 beim linearen Modell gibt, während beim Berner Modell seit 1980 ein Trend eine relative Verringerung des Senkenverhältnisses von 0,4% pro Jahr stattfindet, ausgehend von einem Wert, der 1980 noch größer als beim linearen Modell war aber bereits jetzt um einiges geringer, wie aus Abb. 12 hervorgeht.
Die entscheidende Frage ist nun natürlich, wie sich die echten gemessenen Daten bezügliche dieses Kriteriums verhalten, und damit welches der beiden Modelle eher mit den realen Daten übereinstimmt.
Das Senkenverhältnis der gemessenen Daten
Der entscheidende Test erfolgt mit den echten gemessenen Daten. Mit den Zeitreihen bis Ende 2024 sind, wie mit Abb. 9 gezeigt, die Unterschiede der Modelle bei der Rekonstruktion der gemessenen CO2-Konzentration sehr gering.
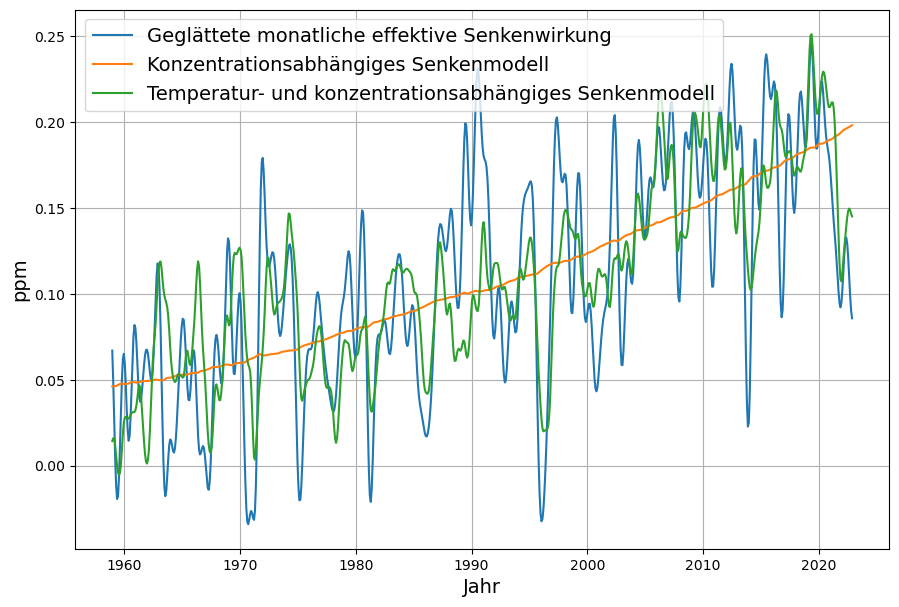
Deswegen werden die aussagekräftigeren Verläufe des gemessenen Senkeneffekts betrachtet. Da sind in der Tat bereits heute leichte Unterschiede erkennbar. Da die gemessene Senkenwirkung (blau) extrem starken kurzfristigen Schwankungen unterliegen, werden diese geglättet (violett). Diese Operation verfälscht den langfristigen Trend nicht. Zum Vergleich werden in Abb 14 die gemessenen Senkenwirkungen als jährliche „Rohdaten“ sowie als deren geglätteter Verlauf im Vergleich zum linearen und Berner Modell dargestellt.
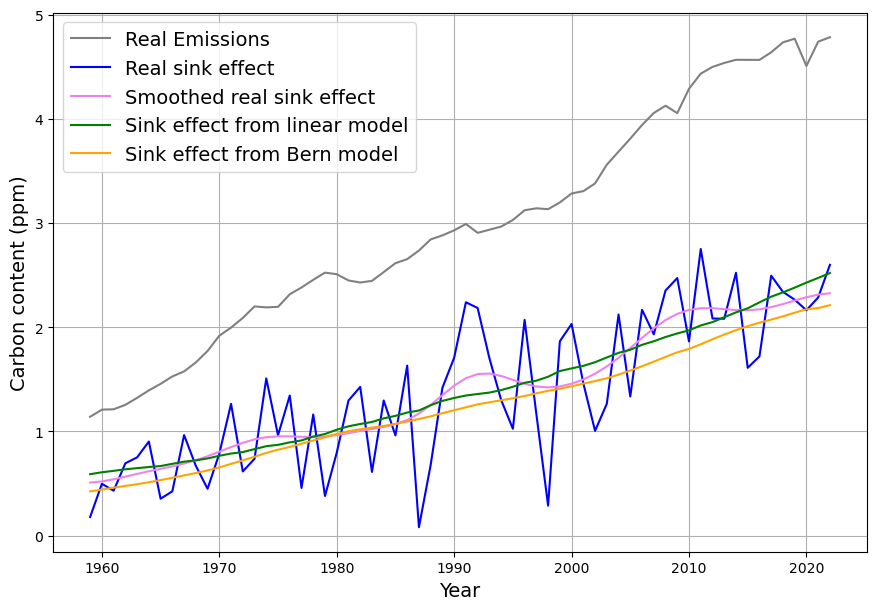
Die Modellwerte beider Modelle sind als Einzelwerte immer noch innerhalb der großen statistischen Schwankungen der gemessenen Senkenwirkung. Aber es deuten sich ganz leichte Trendunterschiede an.
Dies ist aber erst in der Darstellung des Senkenverhältnisses in Abb. 15 deutlicher erkennbar:
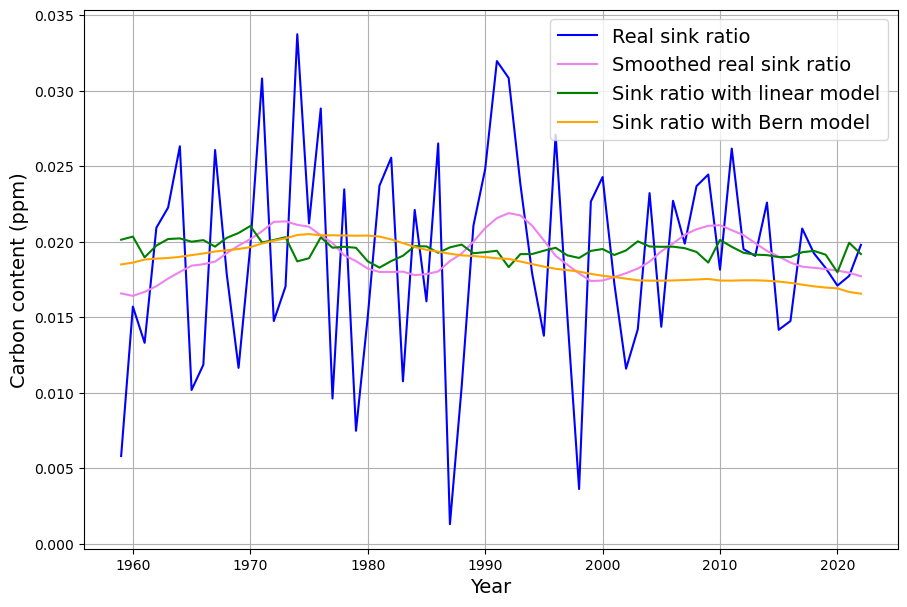
Das Senkenverhältnis der geglätteten gemessenen Senkenwirkung wird im Zeitraum 1980-2022 durch eine Gerade appoximiert, deren Steigung mit Standardfehler berechnet und in ein gemeinsames Diagramm (Abb. 16) mit den Ergebnissen der beiden Modelle eingetragen wird.
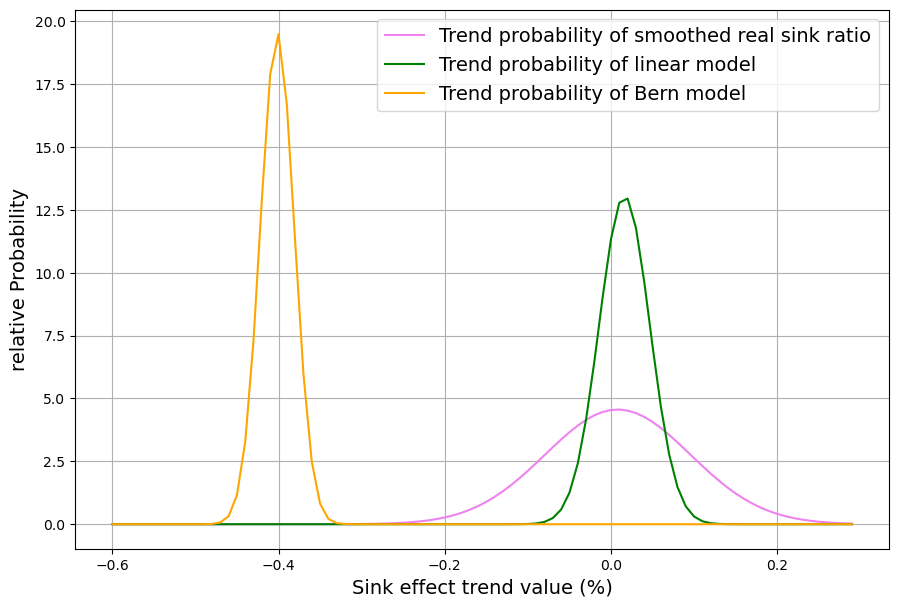
Das Ergebnis ist unmissverständlich. Mit der gemessenen Senkenwirkung der letzten 4 Jahrzehnte ist nur das lineare Senkenmodell kompatibel. Entgegen dem oberflächlichen Augenschein kann das bereits seit 1980 einsetzende Nachlassen der relativen Senkenwirkung des Berner Modells nicht mit den gemessenen Werten in Übereinstimmung gebracht werden. Demnach ist das Berner Modell nicht mit der Realität kompatibel.
Das gleiche gilt auch für die anderen Modelle wie das Budgetmodell (da ist die Abweichung von der Realität noch deutlich größer als beim Berner Modell) oder auch für das oben beschriebene 2-Boxen Modell. Nur das lineare Senkenmodell ist mit den realen Daten der letzten 45 Jahre zur Deckung zu bringen. Nicht untersucht wurde z.B. ein 2-Boxen Modell, bei dem die 2. Box nicht 3 mal sondern z.B. 50 mal größer ist als die erste. Es ist zu erwarten, das solche „fast-linearen“ Modelle auch mit den gemessenen Daten verträglich sind.