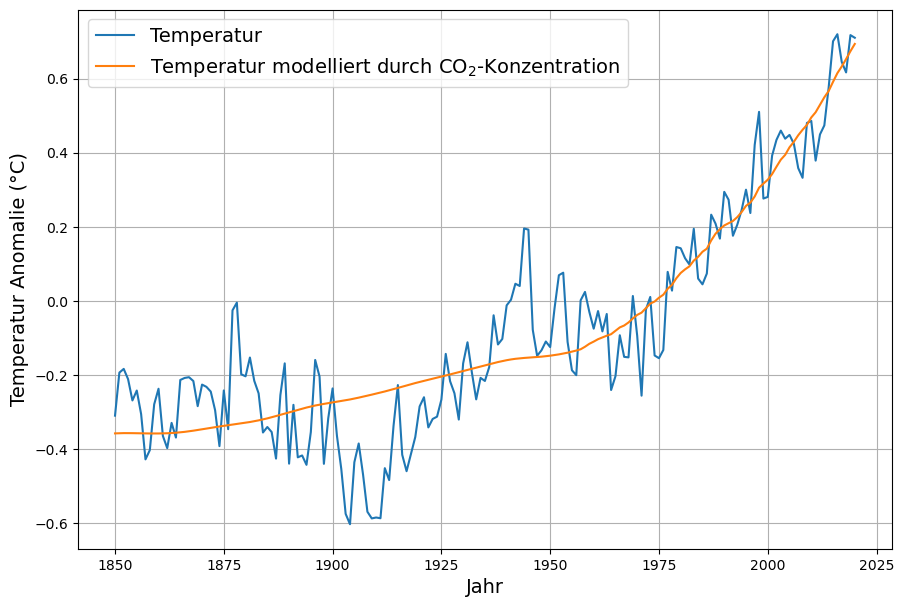
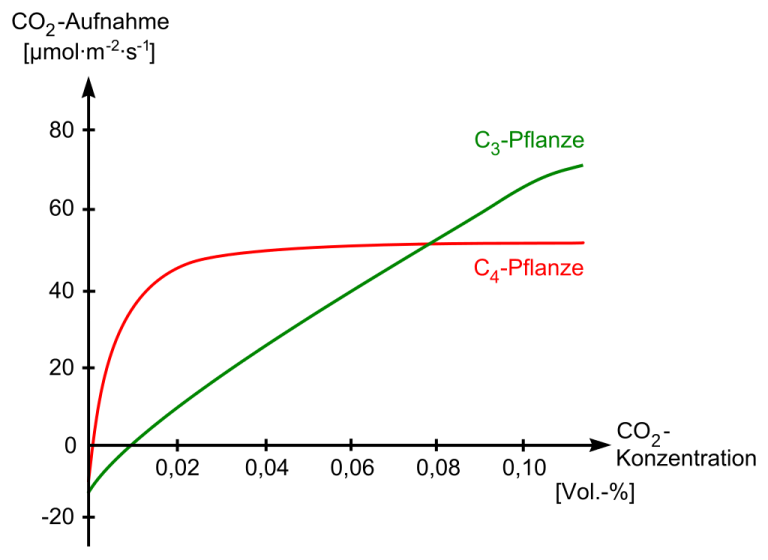
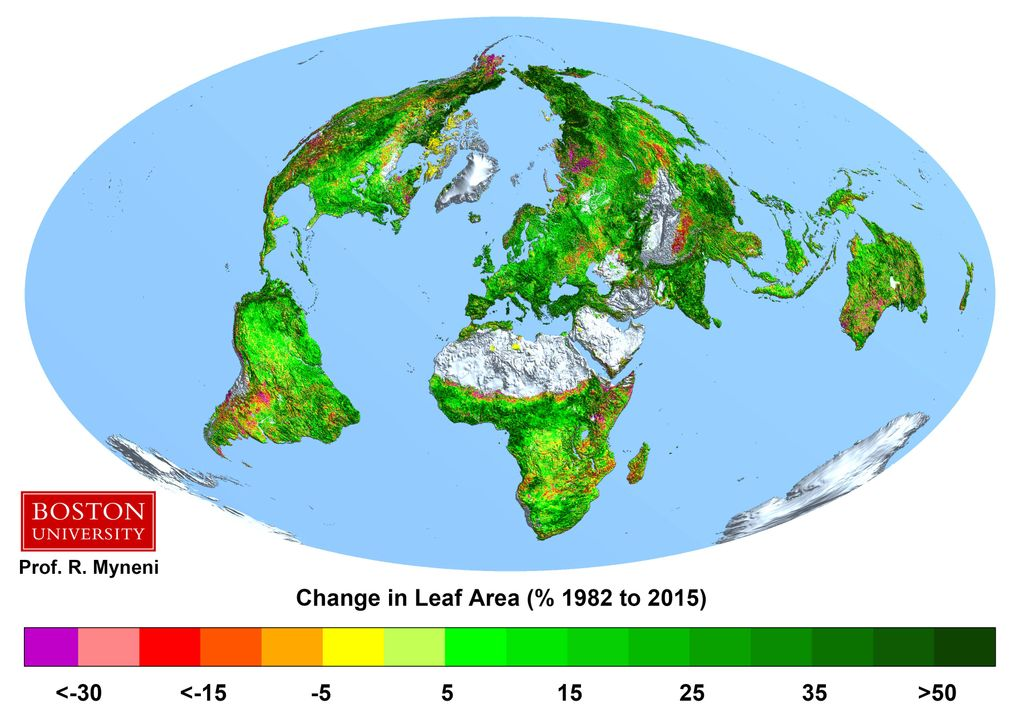
Die Dekonstruktion des Klimanarrativs
Einleitung – Wie funktioniert das Klimanarrativ?
Zweifellos gibt es ein von Wissenschaft, Medien und Politik propagiertes Klimanarrativ, wonach wir uns aufgrund der anthropogenen CO2 Emissionen auf einem Katastrophenkurs befinden, der angeblich nur mit einer Reduktion der Emissionen auf Null bis zum Jahre 2050 aufzuhalten ist.
Alle die dem Narrativ auch nur in subtilen Details widersprechen, werden wie Aussätzige auf „schwarzen Listen“ geführt, selbst wenn sie renommierte Wissenschaftler, ja sogar Nobelpreisträger sind[1][2] – mit verheerenden Folgen für Bewerbungen, Publikationen oder Förderanträge.
Wie ist es möglich, alle wichtigen, auch die renommiertesten Universitäten wie Harvard, MIT und Stanford, Oxford, Cambridge und Heidelberg auf die gemeinsame Konsenslinie zu bringen? Wie kann es gelingen, dass die berühmtesten Zeitschriften wie Nature[3] und Science, aber auch populärwissenschaftliche wie Spektrum der Wissenschaft nur noch einen schmalen „Verständnistunnel“ gelten lassen, ohne ihren Ruf nicht offensichtlich zu ruinieren?
Damit das Narrativ eine solche starke und universelle Wirkung entfalten kann, ist zweifellos ein solides wissenschaftliches Fundament notwendig, das man nicht ohne Blamage bestreiten kann. Diejenigen, die es trotzdem tun, werden auf denkbar einfache Weise als „Klimaleugner“ oder „Wissenschaftsfeinde“ identifiziert.
Auf der anderen Seite sind die Vorhersagen daraus und insbesondere die politischen Konsequenzen daraus dermaßen menschenfeindlich und wirklichkeitsfremd, dass nicht nur eine tiefe gesellschaftliche Spaltung entstanden ist, sondern dass eine zunehmende Zahl von Zeitgenossen, darunter viele Wissenschaftler, hinterfragen, was das für eine Wissenschaft sein soll, die dermaßen abwegige Ergebnisse produziert[4].
Bei sorgfältiger Analyse des Klimathemas findet sich ein Muster, das sich wie ein roter Faden durch alle Aspekte durchzieht. Dieses Muster wird im am Beispiel von 4 Schwerpunkten, die in der Klimaforschung bedeutsam sind, illustriert.
Das Muster, das sich aus langjähriger Auseinandersetzung mit dem Thema herausschälte, besteht darin, dass es im Kern immer eine korrekte Beobachtung oder ein gültiges Naturgesetz gibt. Im nächsten Schritt werden allerdings die Ergebnisse dieser Beobachtung entweder ungeprüft in die Zukunft fortgeschrieben, die Ergebnisse werden übertrieben oder sogar in ihrer Bedeutung verdreht. Andere, zielführende Erkenntnisse werden weggelassen oder ihre Veröffentlichung unterdrückt.
An den genannten und vielen anderen Beispielen lässt sich die typische Schlussfolgerung zeigen, dass bei dem jeweiligen Teilaspekt des Klimas ein möglichst schädliches Ergebnis droht. Das Zusammenfügen mehrerer solcher Komponenten führt in der Summe dann zu den katastrophalen Horrorszenarien, mit denen wir täglich konfrontiert werden. Da die Aussagen meist die Zukunft betreffen, lassen sie sich in der Regel kaum überprüfen.
Die gesamte Argumentationskette des Klimanarrativs hat folgende Form:
- Die anthropogenen Emissionen wachsen – exponentiell.
- Mit den Emissionen wächst die atmosphärische Konzentration an, solange die Emissionen nicht vollständig auf Null reduziert werden
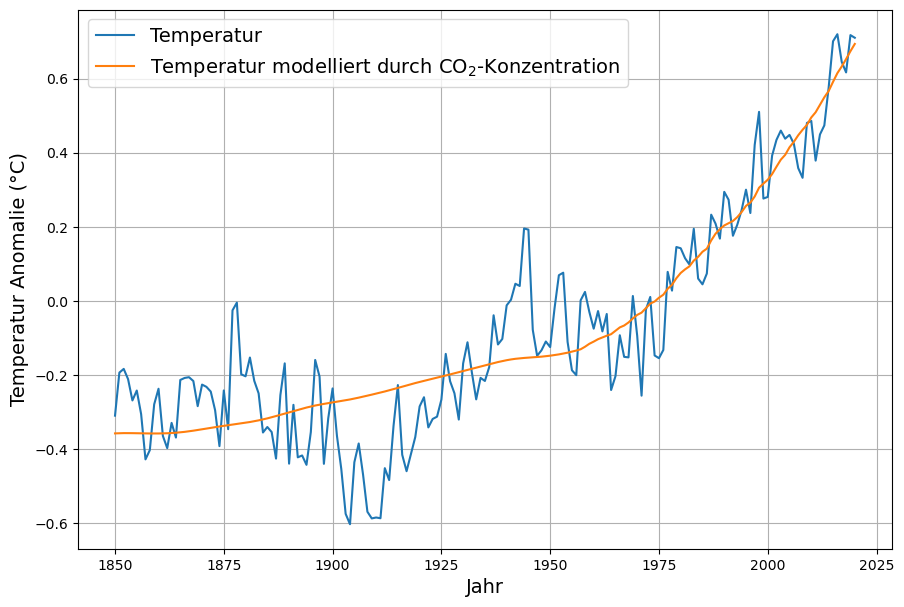
- Das Anwachsen der CO2-Konzentration in der Atmosphäre führt zu einem – dramatischen – Anwachsen der durchschnittlichen Temperatur
- Darüber hinaus gibt es noch positive Rückkopplungen, wenn die Temperatur anwächst, ja sogar Kipppunkte, jenseits derer keine Umkehr mehr möglich ist.
- Andere Erklärungen wie Sonnenstunden oder die damit zusammenhängende Wolkenbildung werden ignoriert, heruntergespielt oder in das System als Rückkopplungseffekt eingebaut.
- Die Auswirkungen sind in der Summe dermaßen katastrophal, dass damit beliebige totalitäre politische Maßnahmen gerechtfertigt werden, mit dem Ziel, die weltweiten Emissionen auf Null herunterzudrücken.
Die ausführliche Beschäftigung mit dem Thema führt zu dem Ergebnis, dass jeder einzelne dieser Punkte das oben beschriebene Muster zeigt, dass es zwar immer einen wahren Kern gibt, der für sich genommen harmlos ist. Den wahren Kern herauszuarbeiten und die Übertreibungen, falschen Extrapolationen oder Weglassen wesentlicher Informationen herauszuarbeiten, ist das Ziel dieser Schrift.
1. Die anthropogenen Emissionen wachsen – exponentiell?
Jeder kennt die klassischen Beispiele exponentiellen Wachstums, z.B. das Schachbrett, das Feld für Feld mit jeweils der doppelten Menge Reis gefüllt wird. Ein exponentielles Wachstum führt grundsätzlich immer in eine Katastrophe. Daher ist es wichtig, die Fakten des Emissionswachstums zu prüfen.
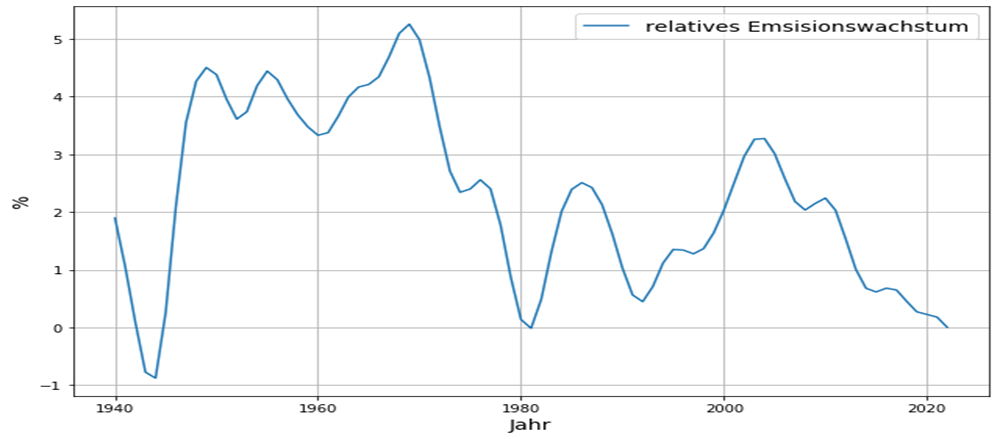
Abbildung 1 zeigt das relative Wachstum der weltweiten anthropogenen Emissionen während der letzten 80 Jahre. Um das Diagramm zu verstehen, vergegenwärtigen wir uns, dass konstantes relatives Wachstum exponentielles Wachstum bedeutet[7]. Ein Sparkonto mit 3% Zinsen wächst im Prinzip exponentiell. Demnach finden wir exponentielles Emissionswachstum mit einer Wachstumsrate von etwa 4,5% zwischen 1945 bis 1975. Diese Phase nannte man einst „Wirtschaftswunder“. Danach ging das Emissionswachstum bis 1980 auf 0 zurück. Man nannte diese Zeit „Rezession“, mit der Konsequenz von Regierungswechseln in USA und Deutschland.
Ein weiterer Wachstumstiefpunkt der Emissionen war um 1990 mit dem Zusammenbruch des Kommunismus verbunden, mit einem folgenden Wiederanstieg, hauptsächlich in den Schwellenländern. Seit 2003 erfolgt eine beabsichtigte Reduktion des Emissionswachstum infolge der Klimapolitik.
Festzuhalten ist, dass aktuell das Emissionswachstum auf 0 gefallen ist.
Vor kurzem hat Zeke Hausfather festgestellt, dass die Summe der weltweiten anthropogenen Emissionen seit 2011 im Rahmen der Meßgenauigkeit konstant[8] sind, dargestellt in Abbildung 2. Demzufolge ist auch für die Zukunft kein Überschreiten der aktuellen Emissionen mehr zu erwarten[9].
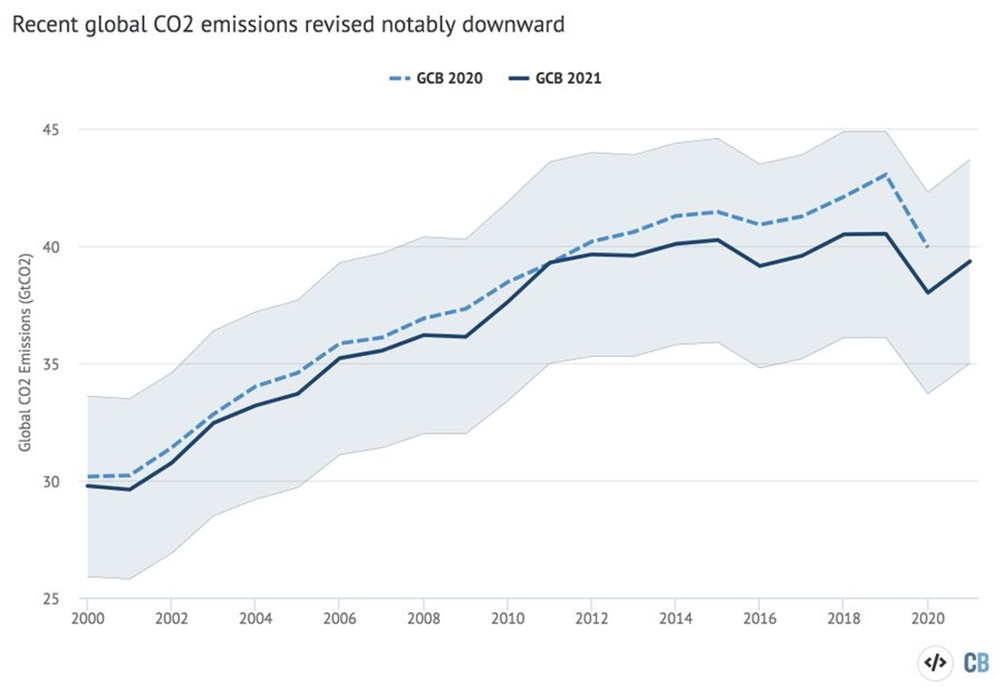
Die längerfristige Fortschreibung der aktuellen geplanten künftigen Emissionen, das sogenannte „Stated Policies“ Szenario (von 2021) erwartet bis 2030 konstante weltweite Emissionen und danach eine ganz leichte Senkung von 0,3% pro Jahr.
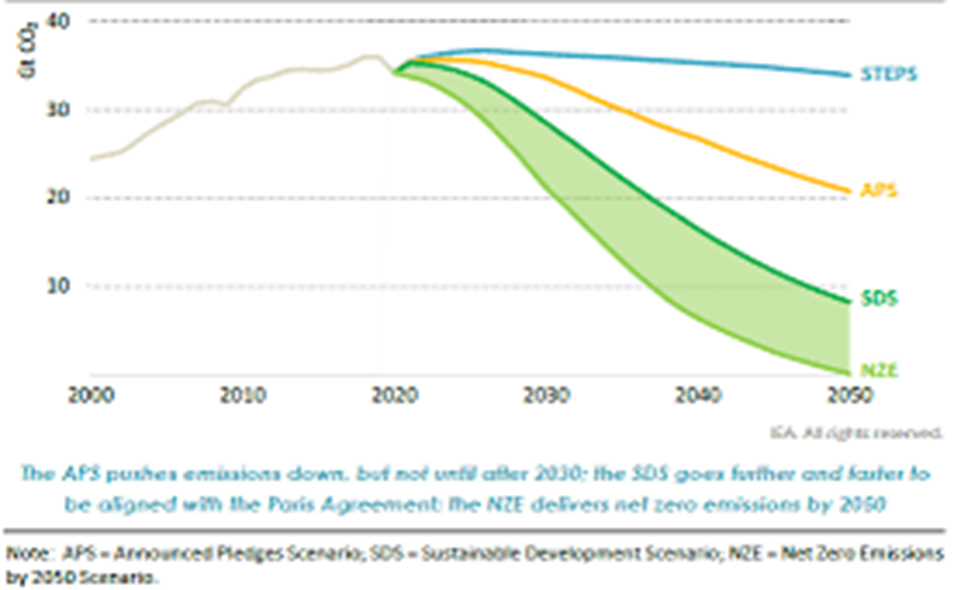
Demzufolge sind die beiden vom IPCC am häufigsten verwendeten Zukunftsszenarien (RCP 8.5 und RCP6.2) fern von der Realität[12] der tatsächlich möglichen Emissionsszenarien. Trotzdem ist das Extremszenario RCP8.5 in den Modellrechnungen immer noch das am häufigsten verwendete[13].
Wissenschaftlich seriös sind vor allem das IPCC Szenario RCP4.5 und diesem in Abbildung 3 dargestellten ähnlichen IEA Szenario „Stated Policies“ (dort S. 33, Figure 1.4)[14].
Damit bleibt es bei Anerkennung der realistischen Emissionsszenarien ohne Infragestellung der vom IPCC verbreiteten Aussagen über das Klima bei einer maximalen emissionsbedingten Temperaturerhöhung von 2,5°C gegenüber dem vorindustriellen Zustand.
2. Atmosphärische CO2 Konzentration steigt kontinuierlich an — es sei denn, die Emissionen werden auf Null reduziert?
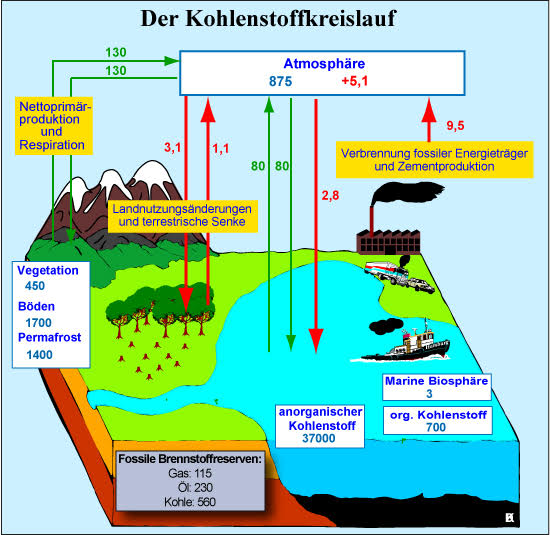
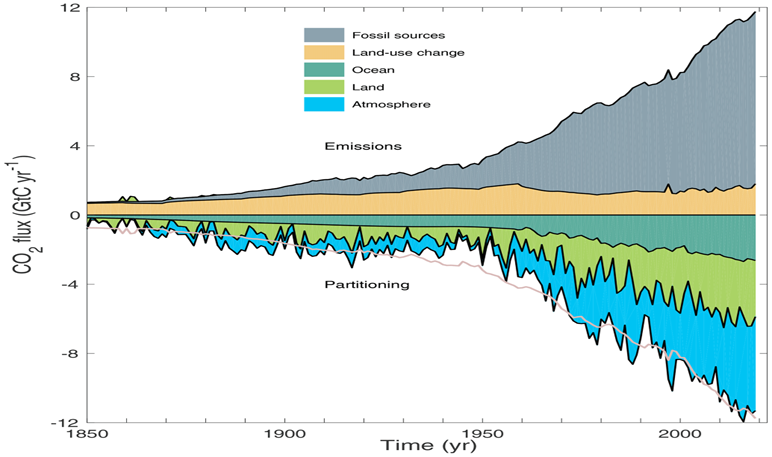
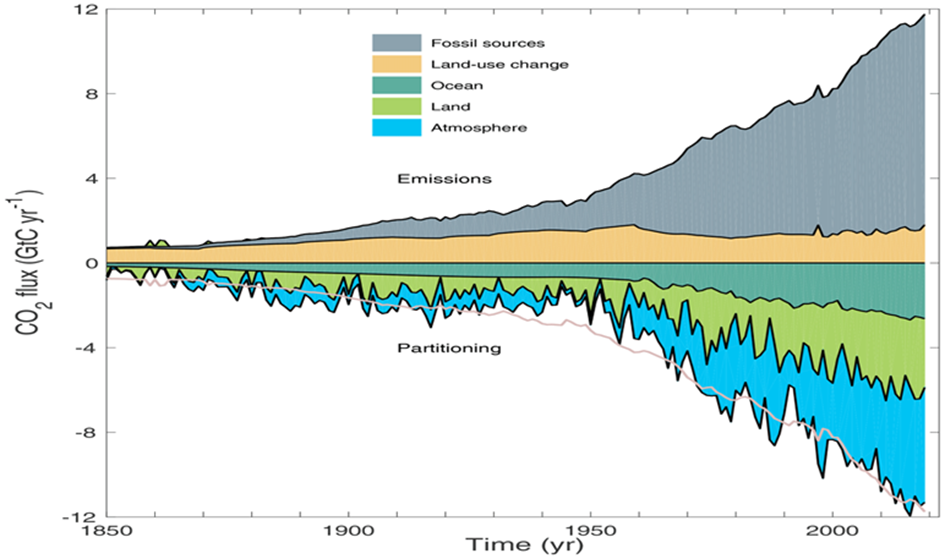
Die Frage ist, wie sich anthropogene Emissionen auf die CO2-Konzentration in der Atmosphäre auswirken. Es ist bekannt und in Abb. 4 von der Internationalen Energieagentur illustriert, dass bei weitem nicht alles emittierte CO2 in der Atmosphäre verbleibt, sondern dass ein wachsender Anteil davon von den Ozeanen und den Pflanzen wieder absorbiert wird.
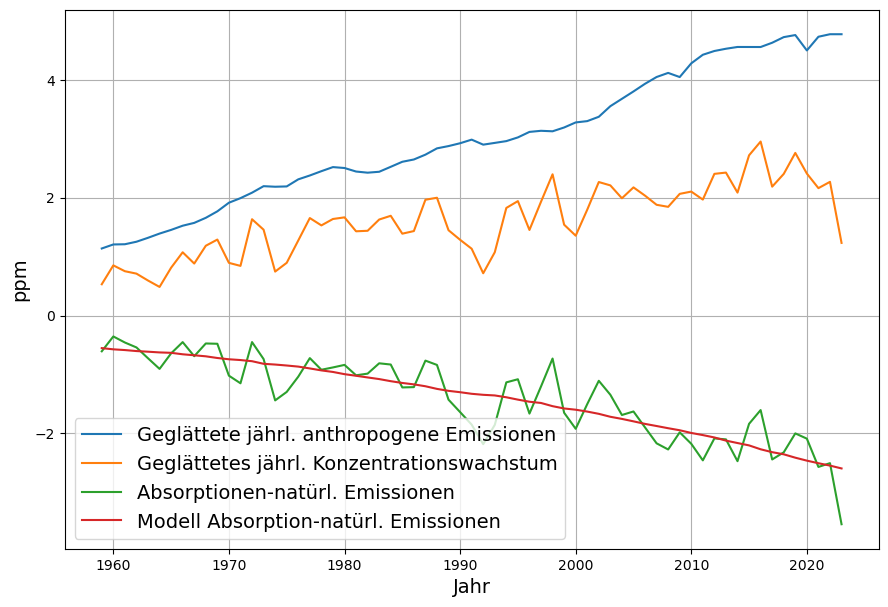
Die statistische Auswertung der anthropogenen Emissionen und der CO2-Konzentration ergibt unter Berücksichtigung der Massenerhaltung und einem linearen Modell der natürlichen Senken Ozeane und Biosphäre, dass jedes Jahr knapp 2% der über das vorindustrielle natürliche Gleichgewichtsniveau hinausgehenden CO2-Konzentration von den Ozeanen und der Biosphäre
(Ozeane und Landsenken) und Konzentrationswachstum in der Atmosphäre
absorbiert werden[15] [16]. Das ist aktuell die Hälfte der anthropogenen Emissionen mit zunehmender Tendenz, wie in Abbildung 5 dargestellt.
Abbildung 5: CO2 Bilanz und lineares Senkenmodell: anthropgene Emissionen (blau),
Konzentrationswachstum (orange), natürliche Senken und deren Modellierung (grün)
Das wahrscheinlichste weltweite Zukunftsszenario der Internationalen Energie Agentur – die in Abb. 3 dargestellte Fortschreibung heutiger politischer Regelungen (Stated Policies Szenario STEPS) – beinhaltet bis zum Ende des Jahrhunderts eine sanften Abnahme (3%/Jahrzehnt) der weltweiten Emissionen auf das Niveau von 2005. Diese Emissionsverringerungen sind durch Effizienzverbesserungen und normalen Fortschritt erreichbar.
Wenn wir dieses STEPS Referenz-Szenario zugrunde legen, führt dies bei Nutzung des linearen Senkenmodells zu einem Anstieg der Konzentration um 55 ppm auf ein Plateau von 475 ppm, wo dann die Konzentration verbleibt.
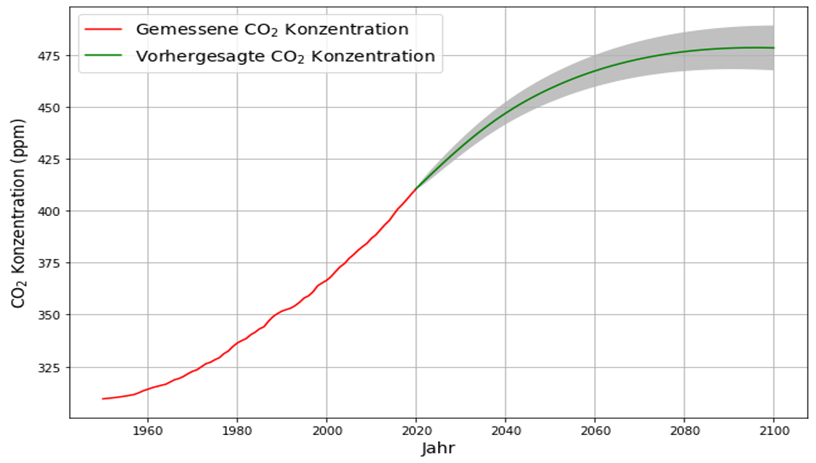
Wesentlich ist, dass dabei die CO2-Konzentration auf keine klimatisch gefährlich hohe Werte steigen wird. Wörtlich heißt es im Pariser Klimaabkommen im Artikel 4.1[17]:
Die Länder müssen ihre maximalen Emissionen baldmöglichst erreichen “um so ein Gleichgewicht zwischen anthropogenen Emissionen von Treibhausgasen und und deren Absorption mittels Senken in der zweiten Hälfte dieses Jahrhunderts zu erreichen”. Das Pariser Klimaabkommen verlangt also keineswegs eine vollständige Dekarbonisierung.
Das Netto-Null Gleichgewicht zwischen Emissionen und Absorptionen wird mit der Fortschreibung heutigen Verhaltens im Jahre 2080 ohne radikale Klimamaßnahmen erreicht.
Ohne auf die Details der sog. Sensitivitätsberechnung einzugehen, lässt sich vereinfacht für die weitere Temperaturentwicklung sagen:
Angenommen, die CO2-Konzentration sei voll verantwortlich für die Temperaturentwicklung der Atmosphäre, dann war 2020 die CO2-Konzentration 410 ppm, also (410-280) ppm = 130 ppm über dem vorindustriellen Niveau. Bis dahin war die Temperatur etwa 1° C höher als vor der Industrialisierung. Künftig können wir mit der obigen Prognose eine Erhöhung der CO2-Konzentration um (475-410) ppm = 65 ppm erwarten. Das ist grade die Hälfte der bisherigen Steigerung. Demzufolge können wir, auch wenn wir von der Klimawirkung des CO2 überzeugt sind, bis dahin zusätzlich die Hälfte der bisherigen Temperaturerhöhung erwarten, also ½° C. Demzufolge wird 2080 die Temperatur mit 1,5° C über vorindustriellem Niveau das Ziel des Pariser Klimaabkommens erfüllen, auch ohne radikale Emissionsreduktionen.
3. Atmosphärische CO2 Konzentration verursacht – dramatischen? – Temperaturanstieg
Nach der Diskussion über die möglichen künftigen CO2-Mengen stellt sich die Frage nach deren Auswirkungen auf das Klima, also nach dem Treibhauseffekt des CO2 und dessen Einfluss auf die Temperatur der Erdoberfläche und der Atmosphäre.
Der mögliche Einfluss des CO2 auf die Erderwärmung besteht darin, dass durch dessen Absorption von Wärmestrahlung diese Strahlung abgeschwächt in das Weltall gelangt. Die Physik dieses Prozesses ist der Strahlungstransport[18]. Da das Thema einerseits grundlegend für die gesamte Klimadiskussion ist, andererseits anspruchsvoll und schwer durchschaubar, wird hier auf die komplizierten physikalischen Formeln verzichtet.
Um den Treibhauseffekt messen zu können, muss die in das Weltall abgestrahlte Infrarotstrahlung gemessen werden. Der erwartete Treibhauseffekt ist aber mit 0,2 W/m2 pro Jahrzehnt[19] so winzig, dass er mit heutiger Satellitentechnologie, die eine Messgenauigkeit von etwa 10 W/m2 hat, nicht direkt nachweisbar ist[20].
Daher hat man keine andere Wahl, als sich mit mathematischen Modellen der physikalischen Strahlungstransportgleichung zu begnügen. Ein gültiger Beweis für die Wirksamkeit dieses CO2 Treibhauseffektes in der realen, sehr viel komplexeren Atmosphäre ist das allerdings nicht.
Es gibt ein weithin anerkanntes Simulationsprogramm MODTRAN[21], mit dem die Abstrahlung von Infrarotstrahlung in den Weltraum und damit auch der CO2-Treibhauseffekt physikalisch korrekt simuliert werden kann:
Abbildung 7 zeigt, dass die MODTRAN Rekonstruktion des Infrarotspektrums hervorragend mit dem aus dem Weltraum gemessenen Infrarotspektrum übereinstimmt. Damit können wir die Anwendbarkeit des Simulationsprogramms rechtfertigen und schließen, dass sich mit der Simulation auch hypothetische Konstellationen mit ausreichender Genauigkeit beschreiben lassen.
Mit diesem Simulationsprogramm wollen wir die wichtigsten Aussagen bezüglich des Treibhauseffekts überprüfen.
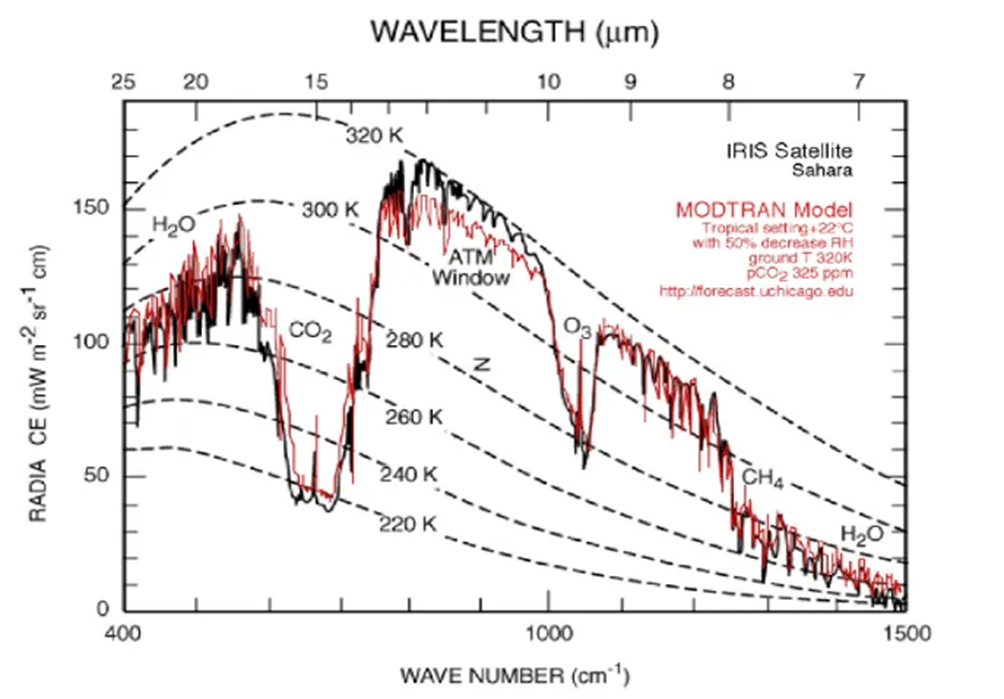
Abbildung 7: Vergleich zwischen gemessenem Infrarot-Spektrum und mit MODTRAN simuliertem Infrarot-Spektrum
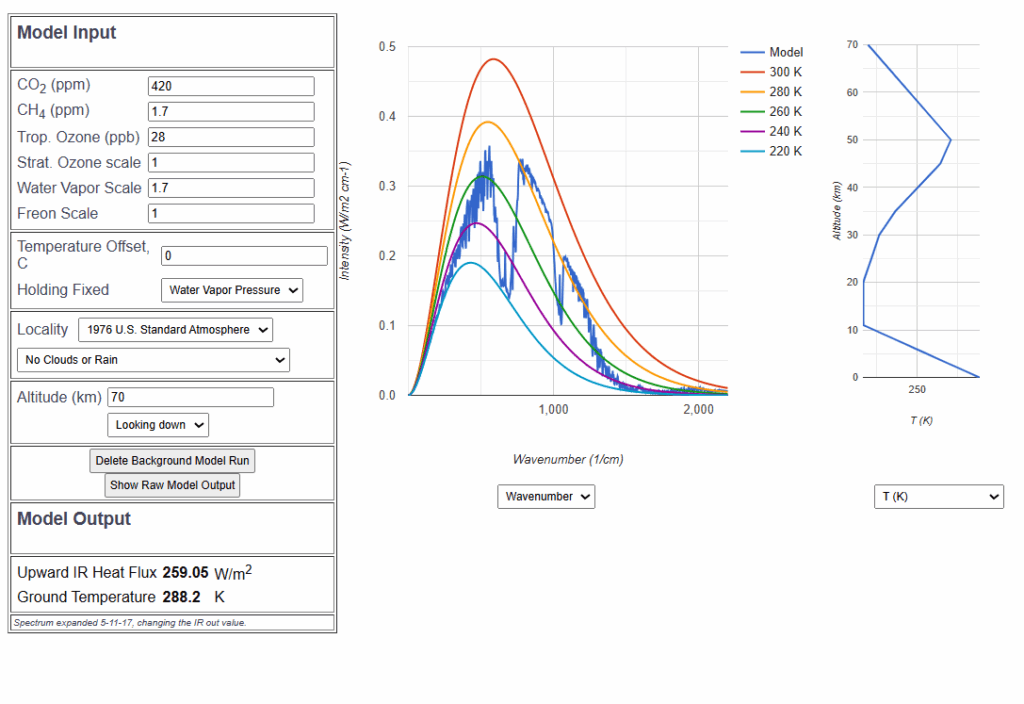
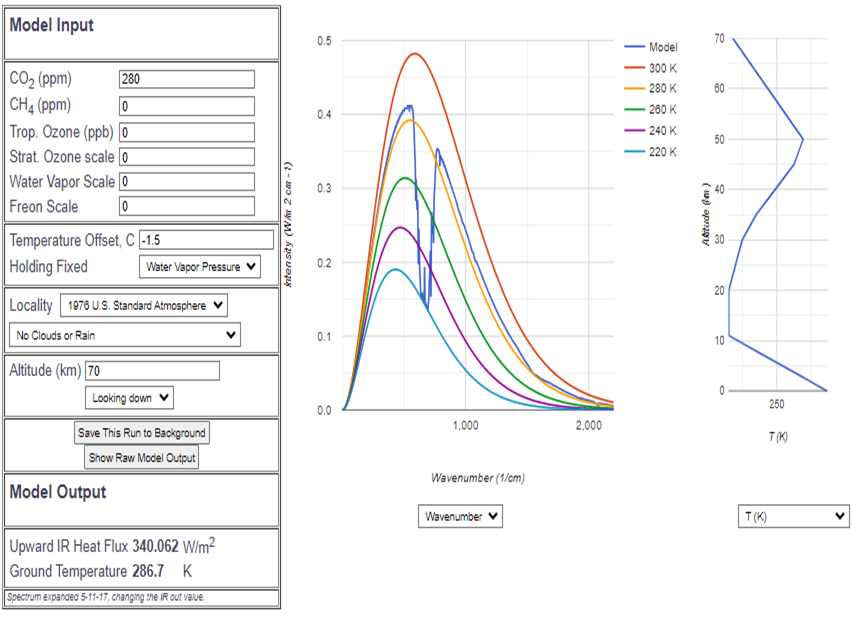
Um auf bekanntem Gefilde zu beginnen, versuchen wir zunächst, den üblicherweise publizierten, „reinen CO2-Treibhauseffekt zu reproduzieren“, indem die durch nichts reduzierte Sonneneinstrahlung die Erde erwärmt und deren Infrarotstrahlung in den Weltraum ausschließlich durch die CO2-Konzentration abgeschwächt wird. Die CO2-Konzentration wird auf das vorindustrielle Niveau 280 ppm eingestellt.
Wir verwenden dabei die sogenannte Standard-Atmosphäre[22], die sich seit Jahrzehnten bei für die Luftfahrt wichtigen Berechnungen bewährt hat, entfernen aber alle anderen Spurengase, ebenso den Wasserdampf. Die anderen Gase wir Sauerstoff und Stickstoff sind aber als vorhanden angenommen, sodass sich an der Thermodynamik der Atmosphäre nichts ändert. Durch leichte Korrektur der Bodentemperatur auf 13,5°C (Referenztemperatur ist 15°C) wird die Infrarot-Abstrahlung auf 340 W/m2 eingestellt. Das ist grade ¼ der Solarkonstante[23], entspricht also genau der auf die ganze Erdoberfläche verteilten Sonneneinstrahlung.
Gut erkennbar ist im Spektrum das „CO2-Loch“, also die gegenüber dem normalen Planck-Spektrum[24] verminderte Abstrahlung im CO2-Band.
Was passiert nun bei Verdoppelung der CO2-Konzentration?

Abbildung 9: Strahlungsantrieb bei Abbildung 9a: Temperaturanstieg zur
CO2-Verdoppelung (keine Albedo, Kompensation des Strahlungsantriebs
kein Wasserdampf) von Abb. 9.
In Abb. 9 ist zu sehen, dass bei Verdoppelung der CO2-Konzentration auf 560 ppm der Wärmefluss der Infrarotstrahlung um 3,77 W/m² vermindert wird. Der von Myhre ermittelte Wert von 3,71 W/m², der mit einer Mischung verschiedener Treibhausgase unter „clear sky“ Bedingungen mit einer Modellrechnung ermittelt wurde, und der auch eine Korrektur aufgrund von Stratosphärenstrahlung enthält, wird vom IPCC und fast allen Klimaforschern verwendet, um den CO2-Antrieb („Forcing“) zu beschreiben. Diese Korrektur, die den Wert geringfügig verändert, ist in der MODTRAN Simulation nicht enthalten. Daher verwende ich, um eine obere Grenze abzuschätzen, als einziges Treibhausgas CO2 ohne Wasserdampf.
In Abb. 9a wird die Bodentemperatur von -1,5°C auf -0,7°C verändert, um wieder die Abstrahlung von 340 W/m2 zu erreichen. Diese Erwärmung um 0,8°C bei Verdoppelung der CO2-Konzentration wird als „Klima-Sensitivität“ bezeichnet. Sie ist, angesichts der aktuellen Meldungen über die drohenden Klimakatastrophen, überraschend gering.
Insbesondere, wenn wir bedenken, dass die bisher verwendeten Einstellungen des Simulationsprogramms völlig an der realen Erdatmosphäre vorbeigehen:
- Keine Berücksichtigung der Albedo, der Rückstrahlung des Lichteinstrahlung,
- Keine Berücksichtigung von Wolken und Wasserdampf
Schritt für Schritt wollen wir uns nun den realen Bedingungen nähern. Die Szenarien sind in Tabelle 1 zusammengefaßt:
| Szenario | Albedo | Einstrahlung (W/m2) |
CO2 vorher (ppm) | Temperatur (°C) |
CO2 nachher (ppm) | Antrieb (W/m2) |
Temperatur- Steigerung fürs Gleichgewicht (°C) |
| Vorindustriell Nur CO2, keine Wolken, kein Wasserdampf | 0 | 340 | 280 | 13,7 | 560 | -3,77 | 0,8 |
| Keine Treib-hausgase, keine Wolken (CO2 von 0-280 ppm) |
0,125 | 297,5 | 0 | -2 | 280 | -27 | 7 |
| Nur CO2, Albedo, keine Wolken, kein Wasserdampf | 0,125 | 270 | 280 | 5 | 560 | -3,2 | 0,7 |
| Vorindustrielle Standard- Atmosphäre |
0,3 | 240 | 280 | 15 | 560 | -2,1 | 0,63 |
| Vorindustrielle Standard Atmosphäre, CO2 heutige Konzentration | 0,3 | 240 | 280 | 15 | 420 | -1,3 | 0,34 |
Das Szenario in der ersten Zeile von Tabelle 1 ist das soeben besprochene „reine CO2“ Szenario.
In der zweiten Zeile gehen wir noch einen Schritt zurück, und entfernen auch noch das CO2, also ein Planet ohne Treibhausgase, ohne Wolken, ohne Wasserdampf. Aber die Erdoberfläche reflektiert Sonnenlicht, hat also Albedo[25]. Der Albedowert 0,125 entspricht dem sonstiger Gesteinsplaneten ebenso wie der Meeresoberfläche. Erstaunlicherweise kommt in diesem Fall eine Oberflächentemperatur von -2° C (und nicht wie oft behauptet -18°C!) zustande. Das kommt daher, dass es ohne Wasserdampf auch keine Wolkenalbedo gibt. Wird nun die CO2-Konzentration auf das vorindustrielle Niveau von 280 ppm erhöht, dann reduziert sich die Infrarot-Abstrahlung um 27 W/m2. Dieser große Strahlungsantrieb wird durch eine Temperatursteigerung von 7°C ausgeglichen.
Wir stellen fest, zwischen dem Zustand ganz ohne Treibhausgase und dem vorindustriellen Zustand gibt es einen stattlichen Treibhauseffekt, mit einer Erwärmung um 7°C.
Die dritte Zeile nimmt diesen vorindustriellen Zustand, also Erdalbedo, 280 ppm CO2, keine Wolken und kein Wasserdampf als Ausgangspunkt für das nächste Szenario. Bei Verdoppelung der CO2-Konzentration beträgt der Strahlungsantrieb von -3,2 W/m2, also etwas weniger als bei dem ersten „reinen CO2-Szenario“. Demzufolge ist auch hier die Erwärmung mit 0,7°C zur Erreichung des Strahlungsgleichgewichts etwas geringer.
Nach diesen Vorbereitungen ist in der 4. Zeile die vorindustrielle Standardatmosphäre mit Albedo, Wolken, Wasserdampf und der real gemessenen Albedo von 0,3 repräsentiert, mit der zur Standardatmosphäre zugehörige Bodentemperatur von 15°C. Die einfachste realitätsnahe Simulation ist eine gewichtete Summe eines wolkenlosen Szenarios mit 21mm niederschlagsfähigem Wasserdampf und ein Wolkenscenario mit der häufigsten Wolkenart (Kumulus) und 28 mm niederschlagsfähigem Wasserdampf. Das wolkenlose Szenario hat das Gewicht 1/3 und das Wolkenscenario hat das Gewicht 2/3. Damit wird eine realistische Abstrahlung erreicht, die im Gleichgewicht zur Einstrahlung von 340 W/m2 . (1-a) = 240 W/m2 ist. Für’s Ergebnis kommt es nicht auf die genaue Wahl dieser Parameter an, allerdings sollte die Abstrahlung 240 W/m2 betragen.
Bei diesem Szenario bewirkt die Verdoppelung der CO2-Konzentration auf 560 ppm einen Strahlungsantrieb von -2,1 W/m2 und eine kompensierende Temperaturerhöhung, also Sensitivität von 0,63°C.
Außer dem Szenario der Verdoppelung der CO2-Konzentration ist natürlich auch von Interesse, was der Treibhauseffekts bis heute bewirkt hat. Die aktuelle CO2-Konzentration von 420 ppm ist gerade in der Mitte zwischen den vorindustriellen 280 ppm und deren doppeltem Wert.
In der 5. Zeile der Tabelle bewirkt die Erhöhung von 280 ppm auf 420 ppm den Strahlungsantrieb von -1,3 W/m2 und die zur Kompensation notwendige Temperaturerhöhung von 0,34°C. Aus diesem Resultat folgt, dass seit dem Beginn der Industrialisierung der bisherige Anstieg der CO2-Konzentration für eine globale Temperaturerhöhung von 0,34°C verantwortlich war.
Das ist viel weniger als die mittlere Temperaturerhöhung seit dem Beginn der Industrialisierung. Daher stellt sich die Frage, wie die „restliche“ Temperaturerhöhung zu erklären ist.
Es bieten sich mehrere Möglichkeiten an:
- Positive Rückkopplungseffekte, die die CO2-bedingte Erwärmung verstärken. Das ist die Richtung des Weltklimarates und Thema des nächsten Kapitels.
- Andere Ursachen wie Wolkenalbedo. Das ist Thema des übernächsten Kapitels
- Zufällige Schwankungen. Gerne wird angesichts des chaotischen Charakters des Wettergeschehens der Zufall herangezogen. Diese Möglichkeit bleibt in Rahmen dieser Abhandlung offen.
4. Rückkopplungen führen zu — katastrophalen? — Konsequenzen
Die im vorigen Kapitel maximal mögliche Klimasensitivität, also Temperaturerhöhung bei Verdoppelung der CO2-Konzentration beträgt 0,8°C, unter realen Bedingungen eher 0,6°C.
Es war in der Klimaforschung schon früh klar, dass eine solch geringe Klima-Sensitivität niemanden in der Welt ernsthaft in Sorge versetzen könnte. Dazu kam, dass die gemessene globale Erwärmung größer ist als von der Strahlungstransportgleichung vorhergesagt wird.
Deswegen wurden Rückkopplungen ins Spiel gebracht, die prominenteste Veröffentlichung in diesem Zusammenhang war 1984 von James Hansen et al.: „Climate Sensitivity: Analysis of Feedback Mechanisms“[26] (Klima-Sensitivität: Analyse von Rückkopplungsmechanismen). James Hansen war es, der mit seinem Auftritt vor dem US-Senat 1988[27] die Klimapolitik der USA maßgeblich beeinflusste. Ähnlich argumentierte Prof. Levermann bei einer Anhörung des Umweltausschusses des Deutschen Bundestags[28], verbunden mit der Behauptung, aufgrund der Rückkopplung würde die Temperatur um 3°C steigen.
Mit Hilfe der Rückkopplungsmechanismen entstanden die vom IPCC veröffentlichten hohen Sensitivitäten bei Verdopplung der CO2 Konzentration zwischen 1,5°C und 4,5°C.
Es stellt sich insbesondere die Frage, wie eine geringe Erwärmung von 0,8°C durch Rückkopplung zu einer Erwärmung von 4,5°C führen kann, ohne dass das System völlig außer Kontrolle gerät?
Die in diesem Zusammenhang mit Abstand wichtigste Rückkopplung ist die Wasserdampf-Rückkopplung. Warum? Weil Wasserdampf per se ein sehr starkes Treibhausgas ist. Allerdings kommt es bei der Rückkopplung nicht auf die Gesamtwirkung an, sondern auf die Wirkung bei kleinen Veränderungen.
Wie funktioniert die Wasserdampf-Rückkopplung?
Die Wasserdampf-Rückkopplung besteht aus einem 2-Schritt Prozess:
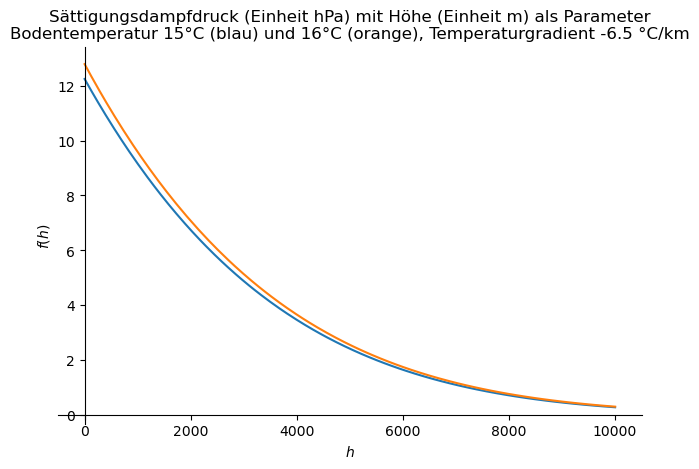
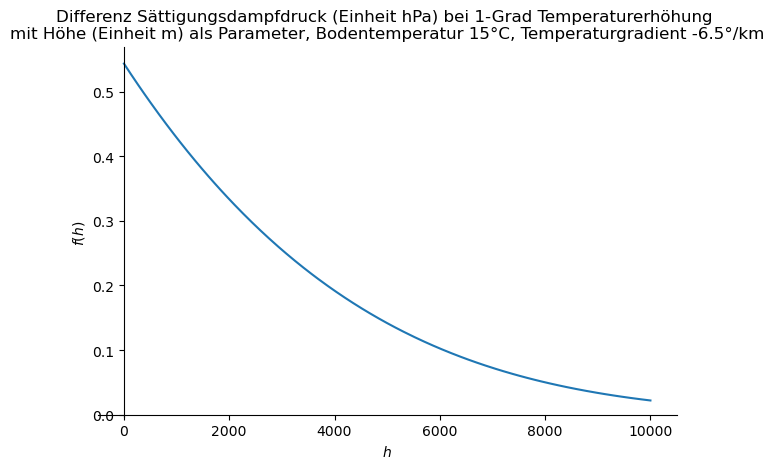
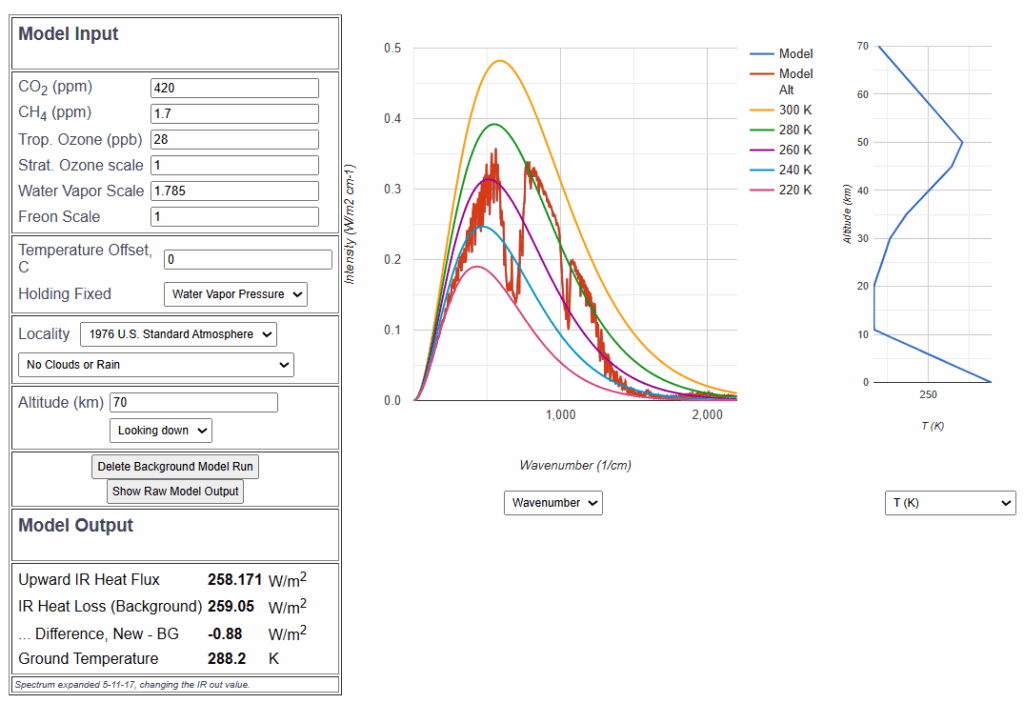
- Wenn die Lufttemperatur um 1°C steigt, kann die Luft um 6% mehr Wasserdampf aufnehmen. Üblicherweise wird ein Wert von 7% angegeben, aber die 7% sind erst ab einer Höhe von 8 km infolge des dort verminderten Luftdrucks möglich. Es ist zu beachten, dass dieser Prozentsatz der maximal mögliche Wasserdampfgehalt ist. Ob dieser wirklich erreicht wird, hängt davon ab, ob genügend Wasserdampf zur Verfügung steht. Nach Tabelle 3 der Publikation „Global Changes in Water Vapor 1979–2020„[29] beträgt die aus Klimamodellen berechnete Sensitivität der Änderung des Wasserdampfes von der Temperatur etwa 5% pro °C Erwärmung. Die Pro Jahrzehnt des Untersuchungszeitraums mit der globalen Erwärmung 0.12°C hat sich demnach der Wasserdampfgehalt um 0,6% erhöht, ausgehend von einer durchschnittlichen niederschlagsfähigen Wasserdampfmenge von 25mm.
- Der Strahlungstransport von Infrarotstrahlung hängt vom Wasserdampfgehalt ab:
Zusätzlicher Wasserdampf reduziert die abgestrahlte Infrarotstrahlung infolge der Absorption durch den zusätzlichen Wasserdampf.
Mit Hilfe des bereits erwähnten MODTRAN-Simulationsprogramms wird unter wolkenlosen Bedingungen und dem globalen Mittelwert von 25 mm niederschlagsfähigem Wasserdampf die wasserdampfbedingte Reduktion der Infrarotstrahlung um 0,88 W/m2 bei Erhöhung des Wasserdampfgehaltes um 5% auf 26,5 mm ermittelt[30].
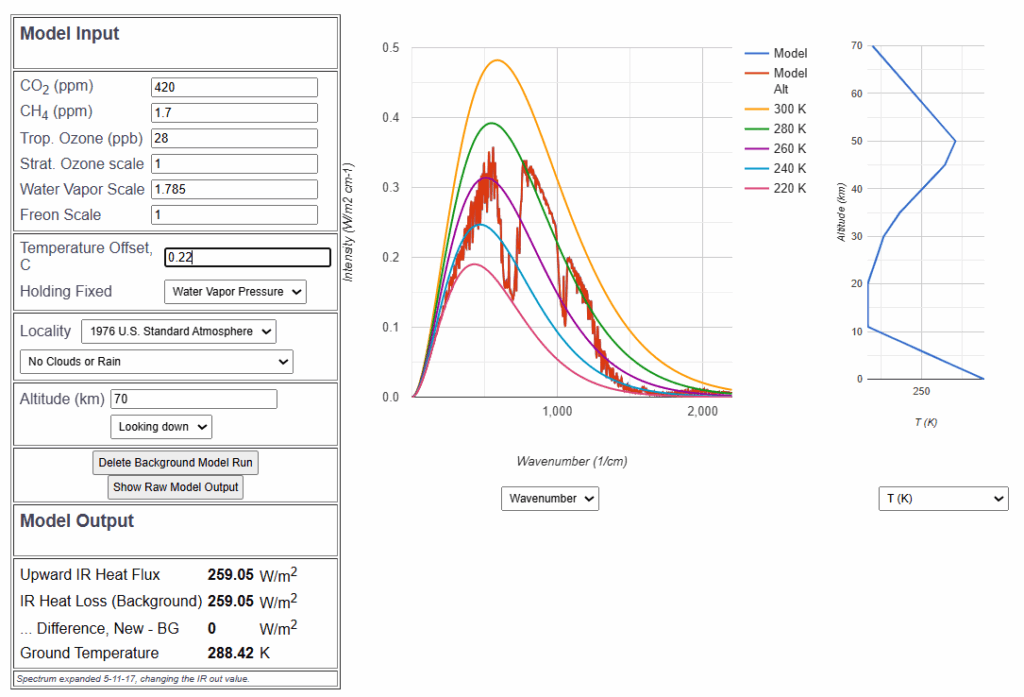
Diese reduzierte Infrarotstrahlung ist ein negativer Strahlungsantrieb. Die diese Abschwächung kompensierende Temperaturerhöhung ist die primäre Rückkopplung g (englisch „gain“). Diese beträgt 0,22 °C als Folge der ursprünglichen Temperaturerhöhung um 1°C, also ist g=0,22.
Die Gesamtrückkopplung f (englisch „feedback“) ergibt sich als geometrische Reihe[31] infolge der rekursiven Anwendung des obigen Mechanismus – die 0,22°C zusätzliche Temperaturerhöhung haben ja eine erneute zusätzliche Wasserdampfbildung zur Folge. Dieser Zusammenhang wird von James Hansen in seiner Arbeit von 1984[32] beschrieben:
f = 1+ g + g2 + g3… = 1/(1-g).
Mit g=0,22 ist demnach der Rückkopplungsfaktor f = 1,28.
Unter Zugrundelegung eines Treibhauseffekts aus dem Strahlungstransport von 0,8°C erfolgt daraus zusammen mit der maximal möglichen Rückkopplung eine Temperaturerhöhung von 0,8°C . 1,28 = 1,0 °C , bei der hier ermittelten Sensitivität 0,63°C . 1,28 = 0,81 °C.
Beide Werte sind niedriger als die kleinste publizierte Sensitivität von 1,5°C der beim IPCC verwendeten Modelle. Die seit dem Beginn der Industrialisierung erfolgte Erwärmung ist demnach selbst mit Rückkopplung 0,34°C . 1,28 = 0,44°C.
Damit ist belegt, dass auch die vielfach beschworene Wasserdampf-Rückkopplung zu keiner exorbitanten und schon gar keiner katastrophalen Klima-Erwärmung führt.
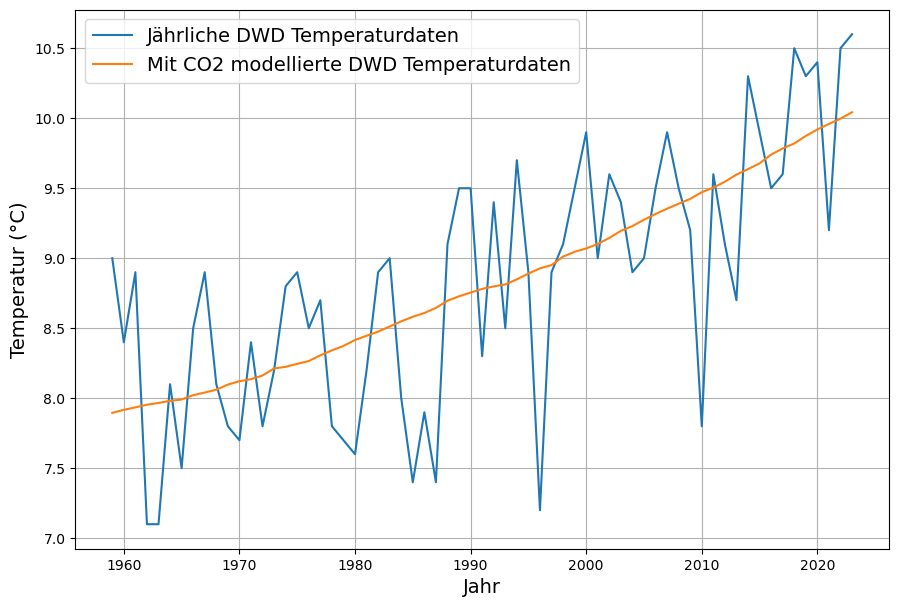
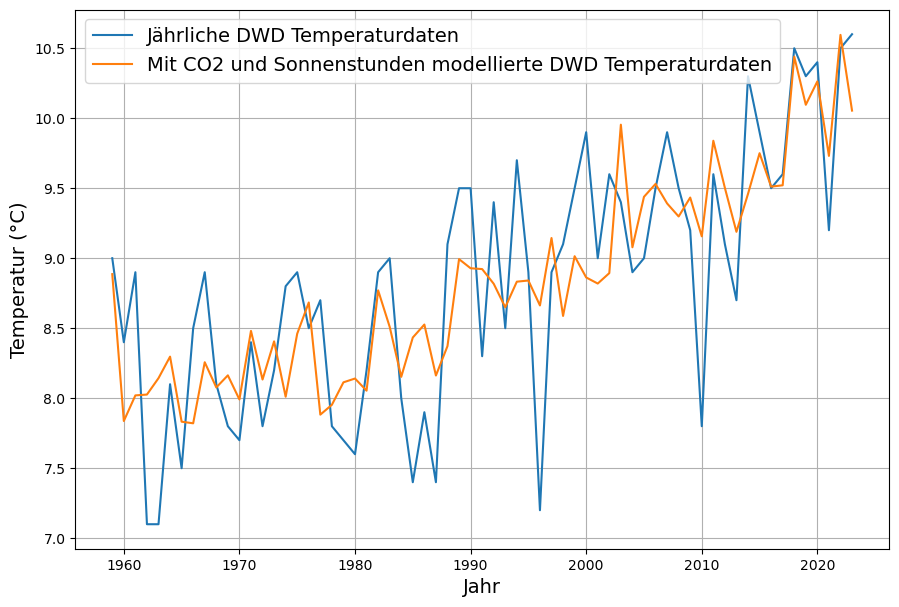
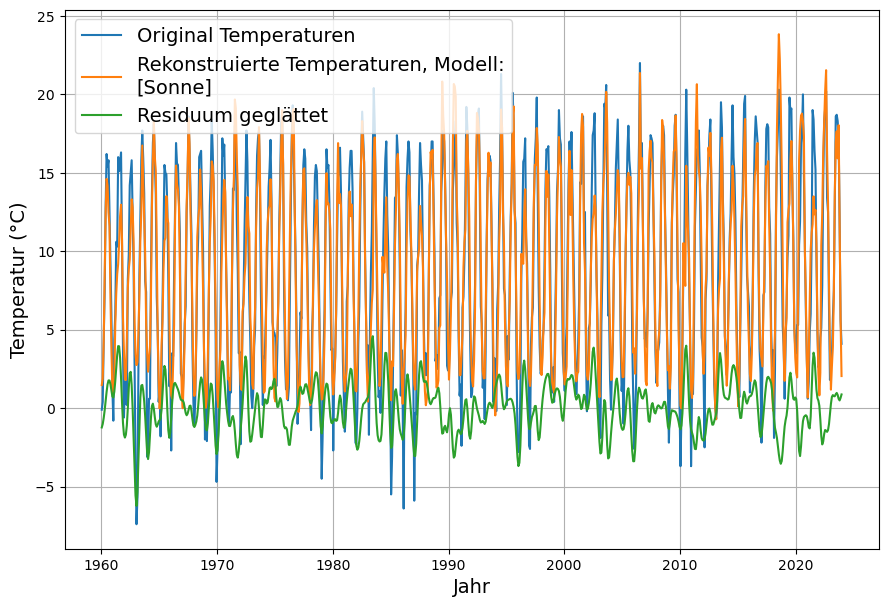
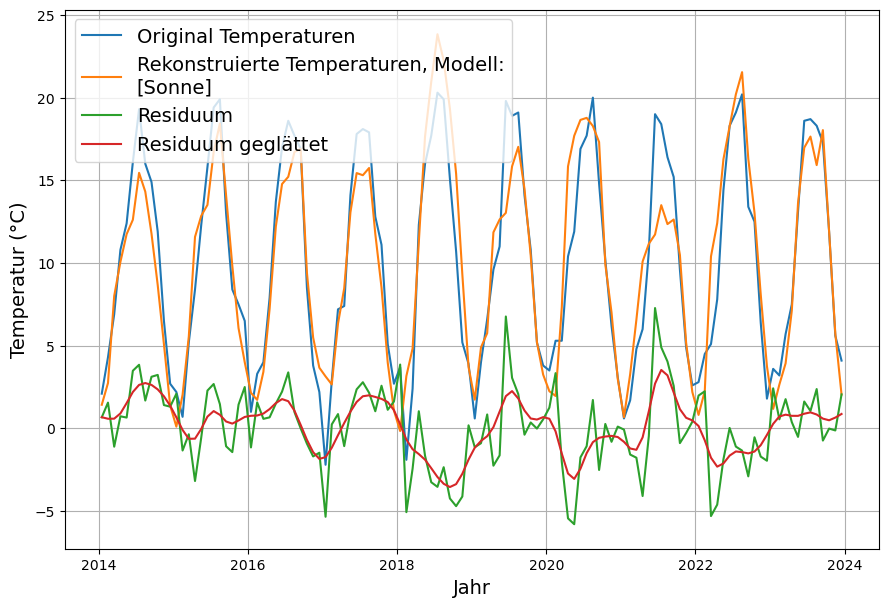
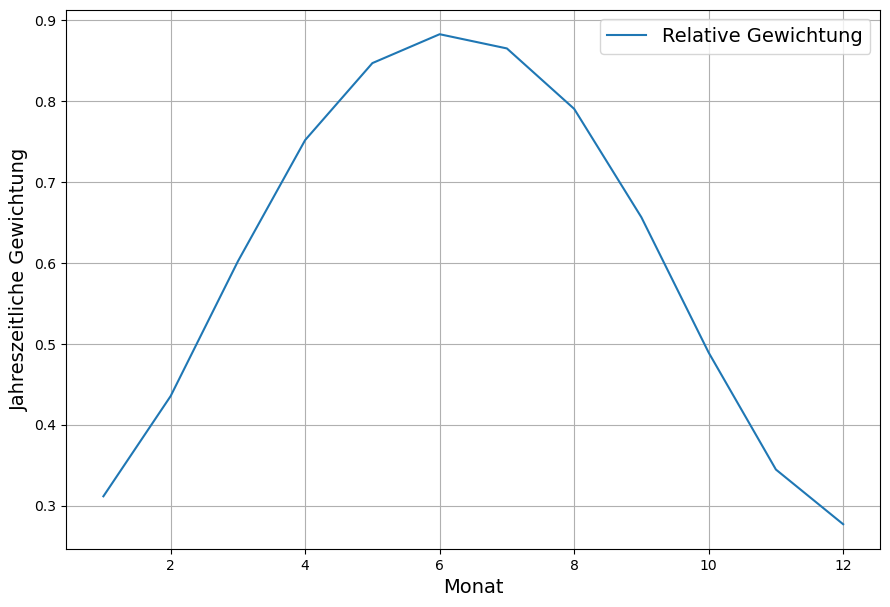
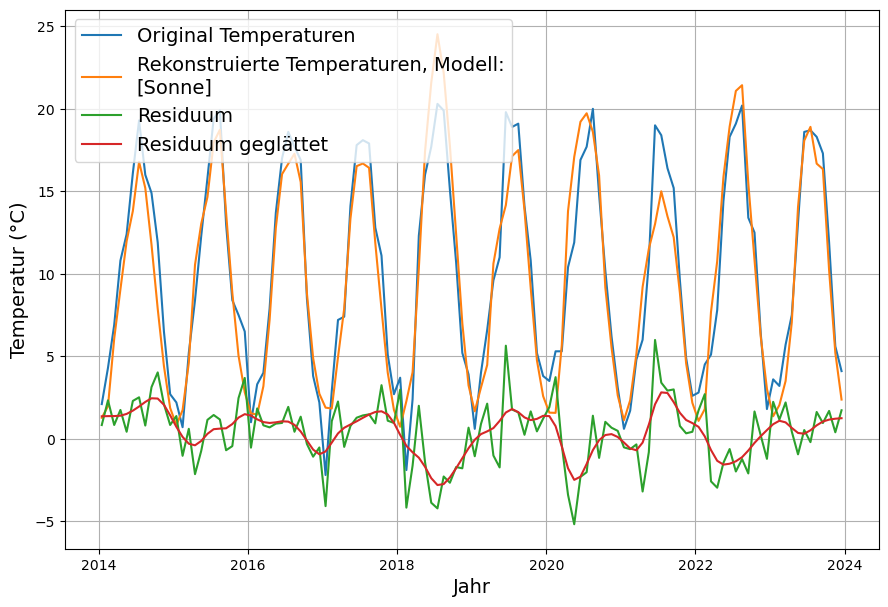
5. Aber sie erwärmt sich doch? – Auswirkungen von Wolken.
An dieser Stelle aufzuhören, wird jeden, der sich mit dem Klimathema beschäftigt, mit der naheliegenden Frage unzufrieden zurücklassen: „Aber die Erde erwärmt sich doch, und zwar stärker, als die nach dem revidierten Treibhauseffekt samt Rückkopplung möglich wäre?“.
Deswegen werden hier die in der Klimadiskussion bis vor kurzem wenig beachteten Auswirkungen der tatsächlichen Wolkenbildung[33] untersucht.
Untersuchung der Veränderungen der weltweiten Wolkenbedeckung
Jay R Herman von der NASA[34] hat mit Hilfe von Satellitenmessungen über einen Zeitraum von mehr als 30 Jahren die mittlere Reflexivität der Wolkenbedeckung der Erde berechnet und ausgewertet:
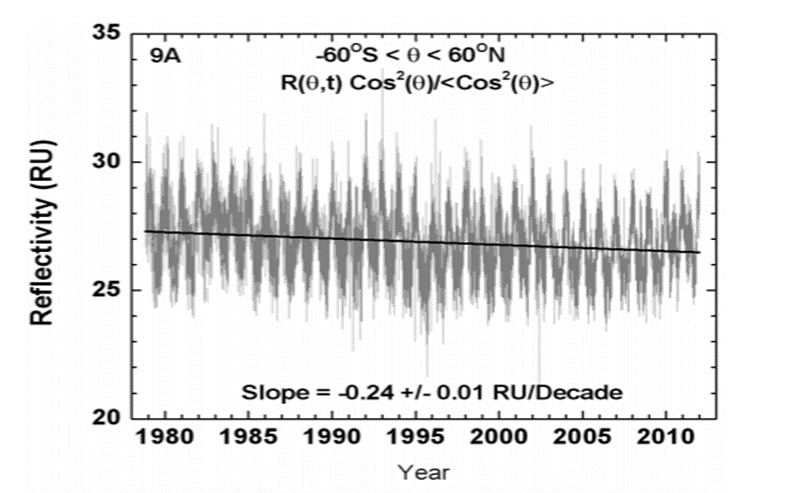
Er stellte einen klaren Trend der Abnahme der Wolkenbedeckung fest. Daraus berechnete er, wie sich dies auf die davon betroffenen Komponenten des globalen Energiebudgets auswirkt:
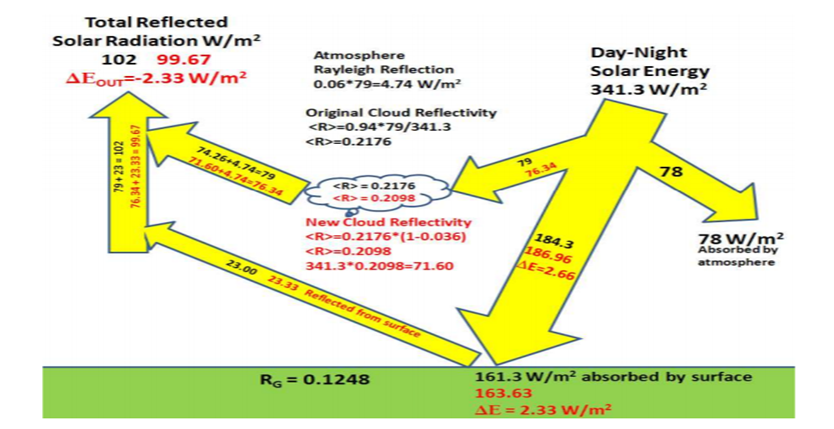
Das Ergebnis war, dass aufgrund der reduzierten Wolkenbedeckung die Sonneneinstrahlung in 33 Jahren um 2,33 W/m2 zunahm. Das sind 0,7 W/m2 Strahlungsantrieb pro Jahrzehnt. Demgegenüber betrug die Abnahme der Abstrahlung infolge der Zunahme der CO2-Konzentration maximal 0,2 W/m2 pro Jahrzehnt[35].
Demzufolge ist nach dieser Untersuchung der Einfluss der Wolken mit 78% auf das Klima mindestens 3,5 mal größer als der des CO2, das demnach allenfalls einen Einfluss von 22% hat.
Fazit – es gibt keine drohende Klimakatastrophe
Fassen wir die Stationen dieser Betrachtungen zur Dekonstruktion des Klimanarrativs noch einmal zusammen:
- Es gibt kein exponentielles Wachstum der CO2-Emissionen. Diese Phase gab es bis 1975, aber die ist längst vorbei, und die weltweiten Emissionen sind seit 10 Jahren auf einem Plateau angelangt.
- Die CO2-Konzentration wächst zwar trotz konstanter Emissionen noch an, aber deren Wachstum hat sich bereits verlangsamt, und wird unter Annahme des wahrscheinlichsten Emissionsszenarios in der 2. Hälfte des Jahrhunderts aufhören.
- Die physikalisch plausible Treibhauswirkung des CO2 ist sehr viel geringer als gewöhnlich behauptet wird, die unter realen atmosphärischen Bedingungen begründbare Sensitivität ist nur 0,5°C.
- Aus der Abschätzung der maximal möglichen Rückkopplungswirkung durch Wasserdampf ergibt sich die obere Grenze des Rückkopplungsfaktors als 1,25. Damit lassen sich keine Temperaturerhöhungen von 3°C oder mehr rechtfertigen
- Es gibt plausible einfache Erklärungen der Temperaturentwicklung der Erde. Die wichtigste davon ist, dass infolge der verschiedenen Maßnahmen der Luftreinhaltung (Reduzierung von Holz- und Kohleverbrennung, Katalysatoren bei Automobilen, etc.) die Aerosole in der Atmosphäre im Laufe der letzten 70 Jahre zurückgegangen ist, was zu einer Verminderung der Wolkenbildung und daher zu einer Erhöhung der Sonneneinstrahlung führte.
[1] https://www.eecg.utoronto.ca/~prall/climate/skeptic_authors_table.html
[2] https://climatlas.com/tropical/media_cloud_list.txt
[3] https://www.cfact.org/2019/08/16/journal-nature-communications-climate-blacklist/
[4] z.B. https://clintel.org/
[5] Rohdaten: https://ourworldindata.org/co2-emissions
[6] Relatives Wachstum: https://www.statisticshowto.com/relative-rate-of-change-definition-examples/#:~:text=Relative%20rates%20of%20change%20are,during%20that%20ten%2Dyear%20interval.
[7] https://www.mathebibel.de/exponentielles-wachstum
[8] https://www.carbonbrief.org/global-co2-emissions-have-been-flat-for-a-decade-new-data-reveals/
[9] https://www.carbonbrief.org/analysis-global-co2-emissions-could-peak-as-soon-as-2023-iea-data-reveals/
[10] https://www.carbonbrief.org/global-co2-emissions-have-been-flat-for-a-decade-new-data-reveals/[
11] https://www.iea.org/data-and-statistics/charts/co2-emissions-in-the-weo-2021-scenarios-2000-2050
[12] https://www.nature.com/articles/d41586-020-00177-3
[13] https://rogerpielkejr.substack.com/p/a-rapidly-closing-window-to-secure
[14] https://iea.blob.core.windows.net/assets/4ed140c1-c3f3-4fd9-acae-789a4e14a23c/WorldEnergyOutlook2021.pdf
[15] https://judithcurry.com/2023/03/24/emissions-and-co2-concentration-an-evidence-based-approach/
[16] https://www.mdpi.com/2073-4433/14/3/566
[17] https://eur-lex.europa.eu/legal-content/DE/TXT/?uri=CELEX:22016A1019(01)
[18] http://web.archive.org/web/20210601091220/http:/www.physik.uni-regensburg.de/forschung/gebhardt/gebhardt_files/skripten/WS1213-WuK/Seminarvortrag.1.Strahlungsbilanz.pdf
[19] https://www.nature.com/articles/nature14240
[20] https://www.sciencedirect.com/science/article/pii/S0034425717304698
[21] https://climatemodels.uchicago.edu/modtran/
[22] https://www.dwd.de/DE/service/lexikon/Functions/glossar.html?lv3=102564&lv2=102248#:~:text=In%20der%20Standardatmosph%C3%A4re%20werden%20die,Luftdruck%20von%201013.25%20hPa%20vor.
[23] https://www.dwd.de/DE/service/lexikon/Functions/glossar.html?lv3=102520&lv2=102248#:~:text=Die%20Solarkonstante%20ist%20die%20Strahlungsleistung,diese%20Strahlungsleistung%20mit%20ihrem%20Querschnitt.
[24] https://de.wikipedia.org/wiki/Plancksches_Strahlungsgesetz
[25] https://wiki.bildungsserver.de/klimawandel/index.php/Albedo_(einfach)
[26] https://pubs.giss.nasa.gov/docs/1984/1984_Hansen_ha07600n.pdf
[27] https://www.hsgac.senate.gov/wp-content/uploads/imo/media/doc/hansen.pdf
[28] https://www.youtube.com/watch?v=FVQjCLdnk3k&t=600s
[29] https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2022JD036728
[30] https://klima-fakten.net/?p=9287
[31] https://de.wikipedia.org/wiki/Geometrische_Reihe
[32] https://pubs.giss.nasa.gov/docs/1984/1984_Hansen_ha07600n.pdf
[33] Beim IPCC werden Wolken in der Regel nur als potentielle Rückkopplungsmechanismen behandelt.[34]https://www.researchgate.net/publication/274768295_A_net_decrease_in_the_Earth%27s_cloud_aerosol_and_surface_340_nm_reflectivity_during_the_past_33_yr_1979-2011
[35] https://www.nature.com/articles/nature14240