Physik des Treibhauseffekts

[latexpage]

Die aktuelle Umweltpolitik scheint nur eine einzige Zielrichtung zu kennen, die Vermeidung des „klimaschädlichen Treibhausgases“ $CO_2$. Dessen schädliche Wirksamkeit wird von „Klimaskeptikern“ und „Klimarealisten“ in Frage gestellt. Die öffentliche Diskussion vermittelt den Eindruck, als könnte diese in Wahrheit schwierige,   wissenschaftliche Frage durch Polemik und Beschimpfungen und durch Mehrheitsbildung in politischen Gremien oder der Wahlurne entschieden werden, mit der fadenscheinigen und grundfalschen Behauptung, die Dinge wären einfach und von der Wissenschaft her völlig geklärt. Umgekehrt verführt die Komplexität des Themas, dessen Details von keiner Einzelperson vollständig überblickt werden, ideologisch voreingenommene Gruppen, mit schwierig durchschaubaren Teil- und Halbwahrheiten die öffentliche Diskussion in Richtung ihrer zweifelhaften politischen Agenda zu dominieren.   

Für mich als Physiker ist diese Situation nicht hinnehmbar. Es ist möglich, auf den Fundamenten der Physik, die seit Jahrhunderten gewachsen sind, und die zum universell akzeptierten Wissen geworden sind, die Frage des Einflusses des Gases $CO_2$ auf die Temperatur der Erde zu klären.
Da gegenwärtig täglich etwa 10 Publikationen zum Thema Klimawandel veröffentlicht werden, kann das Thema hier nicht in allen Einzelheiten behandelt werden.  
Aber aufgrund des Ansatzes, ausschließlich auf unstrittigen Voraussetzungen aufzubauen, sehe ich diesen Beitrag als Chance, das Thema endlich auf sachlicher Ebene anzugehen und zu klären.
Dazu gehört selbstverständlich eine u.U. harte Diskussion, die dann hoffentlich im Geiste dieses Beitrags sachlich und auf den unstrittigen Voraussetzungen aufbauend geführt wird.  Ich gehe davon aus, dass beide „Seiten“ sich an diesen Ausführungen „reiben“ werden. 

Die hier präsentierte Argumentation ist nicht neu, die dazu notwendigen physikalischen Erkenntnisse sind teilweise seit über 100 Jahren bekannt. Die einzelnen Argumente sind auch bereits von anderen Autoren publiziert worden. Was m.E. fehlt, ist eine verständliche, sachliche und 100% nachvollziehbare Argumentationskette.
Wenn ich mich irre, lasse ich mich gerne mit überzeugenden Argumenten eines Besseren belehren, nicht jedoch mit dem unendlich dummen, unwissenschaftlichen Argument, fast alle Wissenschaftler wären sich über bestimmte Aussagen einig.  Das wäre nämlich das Ende jeden wissenschaftlichen Fortschritts.      

Dieser Beitrag hat das Ziel,

• aus unstrittigen physikalischen Voraussetzungen konsequente Schlußfolgerungen zu ziehen,
• die zentrale „Treibhausgas“-These angemessen darzustellen und kritisch zu diskutieren,
• neuere Messungen von Satelliten und anderen Meßeinrichtungen richtig zu interpretieren,
• qualifizierte Stimmen zu Wort kommen zu lassen. 

Wer sich die etwas komplizierte Argumentation mit nicht ganz einfachen physikalischen Formeln ersparen möchte, kann gleich zur Zusammenfassung springen. 

Grundlagen der Atmosphären-Physik

Die folgenden physikalischen Gesetzmäßigkeiten bilden die physikalische Grundlage der Überlegungen zum Einfluß des $CO_2$ auf das Klimageschehen. Implizit kommen darin weitere Naturgesetze zur Geltung (Universelle Gasgleichung, Planck’sche Strahlung, Einstein-Koeffizienten, etc.)

Thermische Zustandsgleichung

Die thermische Zustandsgleichung idealer Gase, oft auch als allgemeine Gasgleichung bezeichnet, beschreibt den Zusammenhang zwischen den thermischen Zustandsgrößen eines idealen Gases. Sie vereint die experimentellen Einzelergebnisse und die hieraus abgeleiteten Gasgesetze zu einer allgemeingültigen Zustandsgleichung: $$p\cdot V=n\cdot R\cdot T$$ mit p: Druck, V: Volumen, n: Anzahl der Mole , T: Temperatur und universelle Gaskonstante $R$: $$R= 8.314463\cdot \frac{m^3 \cdot kPa}{K\cdot mol}$$ Mit Masse m, Molarmasse $M$ und $n=m/M$, sowie Dichte $\rho$ und Molarer Gaskonstante $R_m$ bezogen auf Luft $$\rho=\frac{m}{V} , R_m=\frac{R}{M} = 287.05\frac{J} {K\cdot kg}$$ ergibt sich diese Form der Thermischen Zustandsgleichung: $$p = \rho\cdot R_m \cdot T $$ Also: Dichte multipliziert mit der Temperatur ist proportional zum Druck, wobei die Proportionalitätskonstante nur von der Molmasse der Atmosphäre abhängt.

Barometrische Höhenformel und Adiabatischer Temperaturgradient

Eine wichtige unstrittige Grundlage der folgenden Überlegungen ist der Trockenadiabatische Temperaturgradient (Fachbegriff DALR nach engl. dry adiabatic lapse rate), wonach die Temperatur in der Atmosphäre mit der Höhe abnimmt: $$\Gamma=\frac{dT}{dh} = – \frac{g}{c_p} = – \frac{9.81 \frac{m}{s^2}}{1.005 \frac{J}{gK}} = -9.76 \frac{K}{km}$$ Für den feuchtadiabatischen Temperaturgradienten (Abkürzung MALR oder SALR nach engl. moist bzw. saturated adiabatic lapse rate) gelten zwar ebenfalls adiabatische Bedingungen, doch dabei ausdrücklich für den Fall, dass eine Kondensation von Wasserdampf auftritt. Die im gasförmigen Aggregatzustand enthaltene Kondensationswärme (latente Wärme) von 2257 kJ/kg wird dadurch frei und erhöht die fühlbare Wärmeenergie der Luft. Der trockenadiabatische Temperaturgradient wird durch diese zusätzliche Energiezufuhr – ohne Temperaturänderung — abgeschwächt.  Die anschauliche Erklärung des Temperaturgradienten ist, daß eine Luftmasse überall innerhalb eines Bereiches mit thermodynamischem Gleichgewicht die gleiche Gesamtenergie hat, die Summe aus potentieller Energie aufgrund der Höhe und der inneren Wärmeenergie muß also konstant sein –  Höhe wird mit Temperatur „bezahlt“. 
Damit ergeben sich mit der erweiterten barometrische Höhenformel für Druck und Dichte der wetter- und klimabestimmenden Troposphäre (die unteren 10-12km der Atmosphäre) für den höhenabhängigen Druckverlauf:$$p(h_1) = p(h_0)\cdot(1-\frac{\Gamma\cdot(h_1-h_0)} {T(h_0)})^{\frac{g}{\Gamma R_m}} $$ Mit dem Adiabatenexponent $\kappa$, dem Verhältnis der spezifischen Wärme bei konstantem Druck und bei konstantem Volumen $$\kappa = \frac{c_P}{c_V} = 1.4$$ für trockene Luft gilt dann für die Dichte: $$\rho(h_1) = \rho(h_0)\cdot(1-\frac{\Gamma\cdot(h_1-h_0)} {T(h_0)})^\frac{g}{\Gamma R_m {\Huge \kappa}} $$ Diese Gleichungen bilden die Grundlage der sog. „Standardatmosphäre“, die sich in der Luftfahrt seit Jahrzehnten zuverlässig bewährt hat:

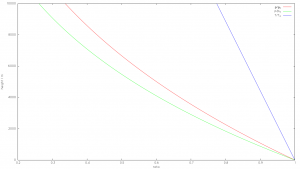
Abb 1: Standardatmosphäre, Verlauf von Temperatur, Druck und Dichte

Die Gleichungen besagen qualitativ, dass

• Temperatur
• Druck
• Dichte

mit zunehmender Höhe strikt abnehmen. Bei der Dichte und dem Druck ist das unmittelbar einsichtig, denn die Atmosphäre wird nach außen hin immer dünner, bis sie ins Vakuum des Weltraums übergeht. Bei der Temperatur ist es weniger intuitiv, aber jedem Bergsteiger ist bekannt, dass die Temperatur pro 100m Höhenanstieg um etwa 1 Grad abnimmt. In feuchter Luft ist es aufgrund der Kondensationswärme des Wassers weniger, im weltweiten Mittel kann beim Temperaturgradienten ungefähr von -6.5 Grad/km ausgegangen werden, bei Schwankungen zwischen -4 Grad/km und -9.6 Grad/km. Entscheidend ist, dass der Temperaturgradient vollständig durch die Gravitation in Form der Schwerebeschleunigung und die spezifische Wärme, ggf. die Kondensationswärme, bestimmt ist.

Diese Gesetzmäßigkeit gilt allerdings nur im lokalen Thermodynamischen Gleichgewicht. Die Temperaturabnahme hört bei der Tropopause auf, weil aufgrund der geringen Luftdichte die Bedingung des Thermodynamischen Gleichgewichts nicht mehr erfüllt ist und die Strahlungseffekte überwiegen. Klimabestimmend ist jedoch die Troposphäre, die durch den Temperaturgradienten definiert wird. Anschaulich bedeutet ein lokales Thermodynamisches Gleichgewicht, dass man mit einem Thermometer die Temperatur messen kann.
Wetterbedingte kurzzeitige und kleinräumige Ausnahmen sind ebenfalls möglich, etwa bei Inversionswetterlagen, deren Ursachen den Meteorologen gut bekannt sind. 

Entscheidend bei der barometrischen Höhenformel ist, dass die Temperatur-, Dichte- und Druckunterschiede alleine aus den beiden Hauptsätzen der Physik und der Annahme des Thermodynamischen Gleichgewichts hergeleitet sind, und für beliebige Gasansammlungen in Gravitationsfeldern gelten, ohne jeglichen Bezug zu eventuellen Treibhausgasen oder äußeren Energiequellen wie der Sonne: Wenn sich eine beliebige Gasansammlung in einem Gravitationsfeld befindet, entsteht (bei einem konstanten Gravitationsfeld und für das Thermodynamische Gleichgewicht hinreichenden Druck von mindestens 0.1 Bar) die durch den adiabatischen Temperaturgradienten und die erweiterte Barometrische Höhenformel gegebene Verteilung von Druck, Dichte und Temperatur.

Damit ist noch nichts gesagt über den absoluten Betrag der Temperatur an der Erdoberfläche. Dieser hängt selbstverständlich von der Sonnen-Einstrahlung und den im weiteren Verlauf zu diskutierenden Faktoren ab. Die höhenabhängigen atmosphärischen Temperaturänderungen im Thermodynamischen Gleichgewicht sind aber ausschließlich durch die Gravitationskonstante und die spezifische Wärme festgelegt.

Konsequenterweise gelten dann auch alle weiteren Schlussfolgerungen für sämtliche Planeten des Sonnensystems. Damit lassen sich die sich hier ergebenden Schlussfolgerungen überprüfen.

Einige Veröffentlichungen der Klimaforschung nähren den Verdacht, dass deren Autoren der Auffassung sind, dass Treibhausgase für den Temperaturverlauf in der Atmosphäre verantwortlich sind. Dem muss entschlossen widersprochen werden. Es gibt keinen wissenschaftlichen Grund, für den Temperaturgradienten eine andere Ursache als die Energieerhaltung (1. Hauptsatz der Physik) und die Annahme des Thermodynamischen Gleichgewichts zu postulieren. Dies ist der Zustand maximaler Entropie im Sinne des 2. Hauptsatzes der Physik. Für die klimarelevanten Betrachtungen genügt es, ein lokales Thermodynamisches Gleichgewicht anzunehmen.

Strahlungstransportgleichung

Eine zentrale Rolle bei der Frage des Einflusses von Treibhausgasen spielt das sog. „Radiative Forcing“, die Temperaturerhöhung der Erdatmosphäre und der Erdoberfläche durch Absorption von Infrarotstrahlung durch Treibhausgase und Re-Emission dieser angeregten Moleküle. Daher ist es notwendig, die Interaktion zwischen Strahlung und Treibhausgasen genauer zu betrachten.

Die Absorption, Streuung und Emission von elektromagnetischer Strahlung in einem Medium wird beschrieben durch die Strahlungstransportgleichung.  Diese Gleichung ist hoch komplex und ich verzichte hier auf deren Details. Für die folgende Argumentation sind folgende unstrittigen Eigenschaften der Strahlungstransportgleichung wichtig:

Die Absorption von Strahlung steigt mit wachsender Dichte des Mediums. Die Emission von Strahlung steigt mit wachsender Temperatur des Mediums.

Die Abschwächung der auf die Erde und in die Erdatmosphäre treffende Sonnen-Einstrahlung aufgrund von Reflexion wird mit Hilfe des sog. Albedo-Faktors a vorgenommen (0..1). Mit dem Anteil a wird Strahlung wieder in den Weltraum reflektiert,  (1-a) ist der Anteil der aktiv wirksamen Strahlung. Die gemessene Albedo der Erde schwankt zwischen 0.2 (=20% Reflexion) am Äquator und 0.7 (=70% Reflexion) an den Polen. Die mittlere Albedo der Erde ist etwa 0.3.
Abb. 2 zeigt, in welchen Wellenlängenbereichen die verschiedenen Luftbestandteile Strahlung absorbieren.

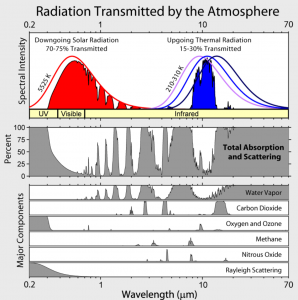
Abb 2: Absorption der Luftbestandteile

Stefan-Boltzmann-Gesetz

Das Stefan-Boltzmann-Gesetz ist ein physikalisches Gesetz, das die thermisch abgestrahlte Leistung eines idealen Schwarzen Körpers in Abhängigkeit von seiner Temperatur angibt $$ P= \sigma \cdot A\cdot T^4 $$ mit P: Strahlungsleistung, A: Querschnittsfläche, T: absolute Temperatur, $\sigma$ Stefan-Boltzmann-Konstante (Definition und Werte der Naturkonstanten im Wikipedia Artikel): $$\sigma = \frac{2 \pi^5 k_B^4}{15 h^3 c^2}= 5.670374 \cdot 10^{-8} \frac{W} {m^2 K^4} $$ Vereinfachende Annahme: Es wird üblicherweise, so auch hier angenommen, daß sowohl die Sonne als auch die Erde sich wie ideale Schwarze Körper verhalten. Für differenziertere Berechnungen wird das Plancksche Strahlungsgesetz verwendet. 
Die flächenbezogene Sonnen-Einstrahlung am Rand der Erdatmosphäre wird als konstant angenommen und als Solarkonstante S bezeichnet: $ S=1370\frac{W} {m^2}$

Theoretische Oberflächentemperatur der Erde

Unter der Annahme eines stationären Zustandes ist die von der Sonne einfallende Strahlung gleich der von der Erde abgehenden Strahlung. Damit ergibt sich sehr vereinfacht formal als theoretische Oberflächentemperatur der Erde: $$T=\sqrt[4]{\frac{S\cdot(1-a)}{4\cdot\sigma}} = 255K$$ Diese theoretische Temperatur ist um 33 Grad niedriger als die tatsächliche mittlere Temperatur von 288K (=15 Grad Celsius). Die dieser Rechnung zugrunde liegende Modellvorstellung eines Schwarzen Körpers ohne Atmosphäre ist allerdings in sich in zweierlei Hinsicht inkonsistent:

• Die Albedo stammt zu einem großen Teil von den Wolken, Wolken gibt es aber nur in einer Atmosphäre, daher sollte die „Basistemperatur“ ohne Wolkenalbedo, nur mit der „Oberflächenalbedo“ von etwa $a=0.14$ berechnet werden, mit der  Gleichgewichtstemperatur $T=268 K$. Damit wäre der „Atmosphäreneffekt“ nur noch 20 Grad. 
• Die Einstrahlung auf die Erdoberfläche ist nicht, wie das Modell suggeriert, homogen, sondern stark inhomogen. Die Pole erhalten nicht nur sehr viel weniger Einstrahlung (in der Polarnacht gar keine) als am Äquator, die Albedo ist dort auch sehr viel höher.  

Daher muss eine sorgfältige Berechnung die statische und dynamische Wirkung der Atmosphäre ebenso wie die breitengradabhängige Einstrahlung berücksichtigen.
Das letztere Thema  würde allerdings den Rahmen dieses Beitrags sprengen und muss auf einen zukünftigen Artikel verschoben werden.  
Ferner bleiben vorläufig das komplexe Wettergeschehen und der wichtige Einfluss der Energiespeicherung in den Meeren und der Einfluss der Luft- und Meeresströmungen unberücksichtigt.  

Erklärung der Temperaturdiskrepanz durch „Radiative Forcing“

Es gibt unzählige Quellen des „Treibhaus“-Ansatzes, die sich auch in Einzelheiten unterscheiden.
Eine Kernaussage des veröffentlichten „Treibhaus“-Ansatzes ist die, daß ein Teil der von der Erdoberfläche ausgestrahlten Wärme durch die Treibhausgase, insbesonders $CO_2$, durch Strahlungseffekte, also Absorption und Emission wieder Richtung Erdoberfläche zurücktransportiert wird. Als repräsentative Referenzen wird auf https://de.wikipedia.org/wiki/Idealisiertes_Treibhausmodell bzw. https://de.wikipedia.org/wiki/Treibhauseffekt verwiesen, woher auch das folgende Diagramm stammt. Dieses Modell wird hier unter dem Thema Strahlungshaushalt beschrieben:

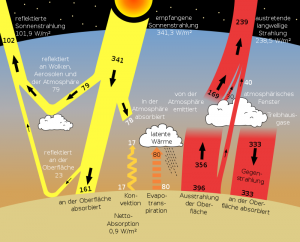
Abb 3: Standard Strahlungs-Modell des IPCC mit Wärmeströmen

Diskussion des öffentlich vertretenen IPCC „Treibhaus“-Ansatzes

Das klassische Treibhaus beruht darauf, dass Wärmekonvektion unterbunden wird durch das Glasdach – bei Öffnen des Glasdaches verschwindet der Treibhauseffekt. Eine solche „Sperre“ gibt es in der Atmosphäre nicht, die Konvektion sorgt für schnellen Ausgleich hin zum lokalen thermodynamischen Gleichgewicht. Der „echte“ Treibhauseffekt hat auch nichts damit zu tun, dass das Glas nicht durchsichtig für Infrarot ist. Bei Verwendung Infrarot-durchlässiger Scheiben ist der Treibhauseffekt fast genau so groß wie bei normalen. Die naive Vorstellung eines Treibhauses ist also für die Atmosphäre nicht anwendbar.

Die atmosphärische „Treibhaus“-Theorie beruht vorwiegend auf Strahlungseffekten des $CO_2$, bei deren öffentlichen Darstellung wird allerdings weitgehend den Umstand ignoriert, dass bis in 10 km Höhe, also in der Troposphäre, der Energieaustausch dominant von der Thermodynamik bestimmt wird, d.h. 67 % Konvektion, 11 % Strahlung, und 22% Kondensation von Wasserdampf.

Ein wesentliches Element des veröffentlichten „Treibhaus“-Ansatzes ist, dass durch das vorhandene $CO_2$ (und andere Treibhausgase) Wärme zur Erdoberfläche „zurückgestrahlt“ wird, die sog. „Gegenstrahlung“. Diese „Gegenstrahlung“ ist aber in der Troposphäre, die sich im lokalen thermodynamischen Gleichgewicht mit weitgehend linearem Temperaturgradienten befindet, synonym mit der Temperatur von treibhausgashaltiger Luft (nach dem Stefan-Boltzmann-Gesetz eines „grauen“ Körpers). Die relative Temperatur wird ausschließlich durch den Temperaturgradienten bestimmt, der seinerseits nur von der Gravitation und der feuchtigkeitsabhängigen Wärmekapazität abhängt, und nicht von irgendeiner Strahlung.  Die absolute Temperatur – der Gesamtatmosphäre – ergibt sich aus dem oben formulierten Strahlungsgleichgewicht bei der „effektiven“ Abstrahlungshöhe. Damit sind sowohl vertikaler Temperaturverlauf als auch das absolute Temperaturniveau physikalisch hinreichend festgelegt, ohne weitere Annahmen. Erst oberhalb der Troposphäre dominieren die Strahlungsprozesse, was daran erkennbar ist, dass der adiabatische Tempereraturgradient nicht mehr gilt.

Es ist richtig, dass durch die von der Erde kommende Infrarot-Strahlung $CO_2$-Moleküle angeregt werden. Die Weitergabe der aufgenommenen Energie kann entweder durch Stöße mit Nachbarmolekülen (Thermalisierung) oder durch Emission erfolgen. Eine Anregung kann auch durch einen Stoß eines Nachbarmoleküls geschehen. In der Troposphäre ist die Weitergabe der Energie durch Stoß sehr viel wahrscheinlicher, weil die mittlere Zeit bis zum nächsten Stoß sehr viel kürzer ist als die mittlere Verweilzeit im angeregten Zustand. Die Abstrahlung bei Emission ist isotrop nach allen Richtungen.

Hinsichtlich der Frage, ob es möglich ist, dass netto eine Strahlung nach „unten“ erfolgt, ist entscheidend, dass die Wahrscheinlichkeit der Strahlungs-Absorption und Emission gemäß der
Strahlungstransportgleichung proportional zur Dichte (und Temperatur bei Emission) der vorhandenen $CO_2$-Moleküle ist. Da aber sowohl die Dichte als auch die Temperatur gemäß der barometrischen Höhenformel mit konstantem Temperaturgradienten von unten nach oben abnimmt, findet netto – unter ansonsten gleichen Bedingungen – ausschließlich ein Wärmetransport von unten nach oben statt. Das ist auch in Übereinstimmung mit dem 2. Hauptsatz der Thermodynamik, wonach Wärme nicht von einem kälteren Körper auf einen wärmeren übertragen werden kann. Nur am Rand — sowohl am oberen wie auch am unteren — tritt die Strahlung der angeregten Randmoleküle teilweise nach außen. Randmoleküle sind solche, die sich weniger als 1 optische Dicke vom Rand (d.h. Weltraum bzw. Erdoberfläche) entfernt befinden.  Am „unteren“ Rand ist ebenfalls die Strahlung von der Erdoberfläche zur Atmosphäre im Mittel größer als umgekehrt, sodaß auch hier der Wärmefluß von unten (wärmer) nach oben (kälter) erfolgt. 

Typische Verweildauern (Lebensdauern) der angeregten Zustände und die mittleren Stoßzeiten bei atmosphärischen Druckverhältnissen in Abhängigkeit der Wellenlänge zeigt die folgende Abbildung:

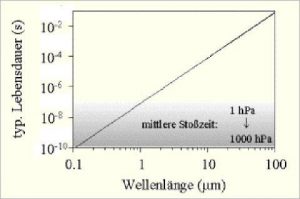
Abb 4: Angeregte Zustände und Stoßzeiten bei $CO_2$

Unter den atmosphärischen Druckverhältnissen stoßen Luftmoleküle nach einer Zeit von $10^{-10}$ bis $10^{-8}$ Sekunden zusammen. (Grauer Bereich). Treibhausgase absorbieren IR-Strahlung (im Bereich 1 – 100 Mikrometer) und werden dabei angeregt. Die Lebensdauer des angeregten Zustandes beträgt in Abhängigkeit von der Wellenlänge zwischen $10^{-7}$ und $10^{-1$} Sekunden, ist also signifikant länger als die Kollisionszeit. Spontane Emission findet daher kaum satt, sondern es kommt durch Kollisionen – mit allen Gasarten – zu einer Lufterwärmung. Die bei dem – entsprechend der Wahrscheinlichkeiten geringen – Anteil der spontanen Emissionen entstehende Strahlung entsteht mit der Resonanzfrequenz des Treibhausgases und wird demzufolge innerhalb der näheren Umgebung wieder absorbiert.

Erklärung der Temperaturdiskrepanz durch „adiabatischen Treibhauseffekt“

Ganz offensichtlich bewirkt die Atmosphäre den Temperaturunterschied von etwa 33 Grad.Der Schlüssel zum Verständnis sind 2 oben besprochene Eigenschaften der Atmosphäre:

1. Die Atmosphäre ist zu einem großen Teil für Infrarot-Strahlung undurchlässig (Abb. 2). Nur etwa 30% können ungehindert abgestrahlt werden. Der Rest wird mittels Absorption überwiegend über die Atmosphären-“Treibhausgase“, v.a. Wasserdampf, $CO_2$ und Methan und Thermalisierung an die Atmosphäre abgegeben. Die Treibhausgase sind dabei austauschbar. $CO_2$ hat keine Sonderrolle im Vergleich zu dem 30-fach häufigeren Wasserdampf, außer dass es Strahlung eines anderen, wesentlich schmaleren Wellenlängenbereichs absorbiert. Und, was noch wichtiger ist, die Wärmeenergie verteilt sich durch Stoßprozesse sofort auch auf die anderen Gase wie Sauerstoff und Stickstoff. Die Energie heizt die Luft dort auf, wo sie absorbiert wird, und wird durch Konvektion, Strahlung und Verdunstung/Kondensation nach und nach an höhere atmosphärische Schichten bei gleichzeitiger adiabatischer Abkühlung übertragen.
   Mit wachsender Höhe und dünnerer Atmosphäre steigt der Anteil der in den Weltraum abgestrahlten Wärmeenergie, weil die absorbierenden Gase dünner werden. Von außen ergibt sich dadurch der adiabatische Treibhauseffekt, indem die Abstrahlung nicht von der Erdoberfläche aus erfolgt, sondern von einer höheren Luftschicht, bei aufgrund des Temperaturgradienten entsprechend niedrigerer Temperatur. 

2. Der Temperaturgradient in der Atmosphäre. Ausgehend von der Gesamtmasse der Atmosphäre stellt sich mit der temperaturabhängigen barometrischen Höhenformel ein weitgehend linear fallender Temperaturverlauf von der Erdoberfläche bis zum Rand der Troposphäre ein. Dieser Temperaturverlauf wird durch die Boltzmann-Verteilung der Energie einer Atmosphäre im planetaren Schwerefeld im Zustand des thermodynamischen Gleichgewichts erzwungen.

Mit der – um der anschaulichen Rechnung willen – extrem vereinfachten Überlegung, dass gar keine Wärmeenergie direkt von der Erde abgestrahlt wird, also dass die Infrarot Strahlungs-Absorption bis zu einer Grenzhöhe vollständig ist, und von dort an schlagartig aufhört, läßt sich eine fiktive Höhe berechnen, von der aus die Abstrahlung in den Weltraum erfolgt – bei der dort vorhandenen Temperatur. Diese Höhe ist frequenz- bzw. wellenlängenabhängig und wird so ermittelt, dass sich bis zum Vakuum des Weltraums eine optische Dicke von 1 ergibt (Hier eine plausible Näherungsrechnung dazu). 
Mit dem üblicherweise angenommenen mittleren Temperaturgradienten von -6.5 K/km herrscht in etwa 5 km Höhe die Temperatur des stationären Gleichgewichts von 255K. Dies ist interessanterweise etwa die maximale Höhe des Wasserdampfes in der Atmosphäre. Eine verfeinerte Rechnung würde ggf. eine andere “effektive Grenzhöhe” ergeben, ändert aber am qualitativen Ergebnis nichts, und würde mindestens ein Modell der Wolken voraussetzen. Diese Herleitung kommt zu demselben Ergebnis wie das bekannte Klimamodell von James Hansen, der ohne es im Detail auszuführen, auch den Temperaturgradienten (lapse rate) voraussetzt. 
Entscheidend für den “adiabatischen Treibhauseffekt” ist der optisch dichte Teil der Gesamtmasse der Atmosphäre (z.B. Hans Jelbring, The “Greenhouse Effect” as a function of atmospheric mass, ohne Berücksichtigung der „optischen Dichte“ ), die “Treibhausgase” spielen dabei zum einen die Rolle eines wellenlängenabhängigen “Katalysators” zur Übertragung der Strahlungsenergie in kinetische Energie (Temperatur), zum anderen entsprechend der Emissionsspektren zur Abstrahlung in den Weltraum.

Interpretation der Infrarot-Emissions-Spektren

Durch Satelliten liegen gemessene Emissionsspektren der Atmosphäre vor, diese sind natürlich orts- und tageszeitabhängig. Es ist wichtig festzustellen, dass die dargestellte Auflösung dieser Spektren ist viel höher ist als was in Wirklichkeit gemessen wurde, das heißt die dargestellten Spektren sind simuliert und an die gemessenen Daten angepßt. Diese Daten bestanden aus 8 Meßwerten, 7 davon aus dem $CO_2$-Band: 

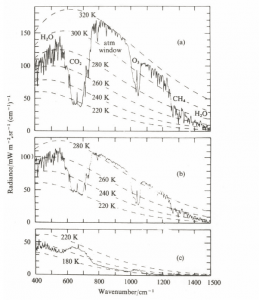
Abb 5: Gemessene Abstrahlungen in der Sahara, Mittelmeer und Antarktis, mit dem Nimbus Satelliten (1971, aus Bergmann-Schäfer, Lehrbuch der Experimentalphysik, Band 7, 1997)

Für die nach oben gerichtete Infrarotstrahlung bedeutet das, dass die vom Boden emittierte Strahlung wegen der starken Absorption fast vollständig verschwindet und durch die Eigenstrahlung derjenigen kälteren Atmosphärenschicht ersetzt wird, die nahe genug am Weltraum ist, um nicht wieder absorbiert zu werden.
Bei einem von Satelliten aufgenommene Spektrum stammt also die Energie je nach Absorber und Wellenlänge aus unterschiedlichen Höhe in der Atmosphäre. Das $CO_2$ absorbiert die Infrarot-Strahlung im Bereich der Wellenzahlen 600-750/cm. Aus dem Absorptionsspektrum ergibt sich, dass in diesem Bereich die Abstrahlung nicht wie sonst von einer Temperatur 255-270 K erfolgt, sondern nur bei 220 K. Aufgrund des Umstandes, dass die Abstrahlung in den Weltraum proportional zur 4. Potenz der Abstrahltemperatur erfolgt, bedeutet das, dass in den $CO_2$-Bereich weniger Energie in das Weltall abfließt. Dies hat zur Folge, dass sich die ganze Atmosphäre ein wenig mehr erwärmt als wenn $CO_2$ nicht vorhanden wäre, und die Energie sich auf alle Wellenlängenbereiche verteilen würde. Ist die „normale“ Abstrahltemperatur niedriger als 220 K, dann ergibt sich durch das Vorhandensein von $CO_2$ ein negativer Treibhauseffekt, im $CO_2$-Band und auch beim Wasserdampf wird mehr Energie abgestrahlt als wenn die „Treibhausgase“ nicht vorhanden wären, und der Effekt ist eine Abkühlung.  Dies ist nicht hypothetisch, in der Antarktis ist der negative Treibhauseffekt nachgewiesen (Abb. 5, siehe auch hier). 
Daher ist der Begriff „Treibhausgas“ sehr irreführend, denn  ob es durch $CO_2$ zu einer relativen Erwärmung oder Abkühlung kommt, oder ob es gar keinen $CO_2$ Einfluss gibt,  hängt von verschiedenen Einflussfaktoren ab. 

CO₂-Sensitivität der Erdatmosphäre

Die entscheidende „Treibhaus“-Frage ist, wie sich die Gesamttemperatur auf diesem Wege verändert, wenn sich der $CO_2$-Gehalt der Atmosphäre verdoppelt von den vorindustriellen 280 ppm auf z.B. 560 ppm. Dies nennt man die $CO_2$-Sensitivität. Der aktuelle $CO_2$ Wert (2019) ist etwa 415 ppm.
Die Zusammenhänge sind kompliziert, und in der öffentlichen Diskussion gehen gerade bei diesem Thema die Überzeugungen sehr auseinander. 
Die „Skeptiker“ teilen überwiegend die Erkenntnis, dass es den hier geschilderten Einfluß des $CO_2$ in der Atmosphäre gibt, aber sie vertreten die Überzeugung, dass

• die $CO_2$-Sensitivität (Erderwärmung bei Verdoppelung des $CO_2$-Gehalts der Atmosphäre) nicht mehr als 1 Grad beträgt (wovon bereits heute 0.6-0.7 Grad wirksam sind),

• andere Einflußfaktoren (Pflanzenwachstum, Wüsten, städtische „Hitzeinseln“) einen Einfluss ähnlicher Größenordnung haben wie $CO_2$, und die u.U. leichter beeinflußbar sind als die zivilisationsbedingte Erzeugung von $CO_2$.

• die Rückkopplungseffekte zwischen $CO_2$, Wasserdampf, Wolken und Weltmeeren sich in der Summe nicht verstärken, sondern gegenseitig abschwächen

Das Ziel hier ist, zunächst eine nachvollziehbare, konsensfähige Aussage zur reinen $CO_2$-Sensitivität zu bekommen. Dies ist überraschenderweise sogar recht einfach, und ich frage mich, warum dieser Weg nicht mehr publiziert wurde.  Allerdings ist das verwendete Modell statisch und sehr einfach und berücksichtigt weder Wettereinflüsse noch Einflüsse der Weltmeere.  Aber der für die Bedeutung des $CO_2$-Einflusses wichtige Strahlungstransports wird gut abgebildet. Und die Zielgröße „abgestrahlte Energie“ erlaubt wegen der Additivität der Energie die Betrachtung an einem Punkt, mit anschließender Mittelung über die ganze Erdoberfläche.    

Der Schlüssel ist das öffentlich nutzbare Programm MODTRAN, das seit vielen Jahren für spektroskopische Untersuchungen, insbesondere in der Klimaforschung eingesetzt wird.
Mit diesem Programm lässt sich das Absorptionsspektrum der Atmosphäre recht zuverlässig modellieren, und damit ist man in der Lage, die Abstrahlung der Erdoberfläche unter Berücksichtigung der Treibhausgase und anderer Bedingungen an jeweils einem Ort zu berechnen. Durch die Wahl der oben beschriebenen Standardatmosphäre und der gemittelten Oberflächentemperatur von 288 K (= 15 Grad C) erhält man ein einfaches globales Modell.

Hier zunächst die Modellierung des atmosphärischen Absorptionsspektrums vor der Industrialisierung, also mit einem $CO_2$-Anteil von 280ppm:

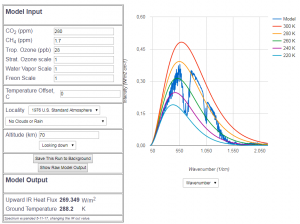Abb 6: MODTRAN Abstrahlungsmodell für 280 ppm $CO_2$-Anteil (Jahr 1850)

Zwischen der Wellenzahl 550 und 770 ist die deutlich sichtbare Absorption durch $CO_2$, was im Vergleich zu völlig fehlendem $CO_2$ einen signifikanten Treibhauseffekt bedeutet, die Minderung der Abstrahlung aufgrund des vorindustriellen $CO_2$ ist etwa 10% der Gesamtabstrahlung. Dies ist aber kein Diskussionsthema, denn mit weniger als 150ppm $CO_2$ Gehalt gibt es kein Leben auf der Erde. Bei der Frage des „menschengemachten“ Treibhauseffekts wird üblicherweise 280 ppm als Ausgangspunkt angenommen.

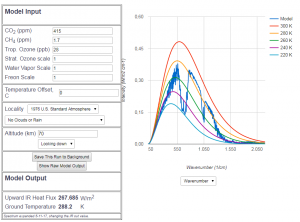
Abb 7: MODTRAN Abstrahlungsmodell für 415 ppm $CO_2$-Anteil (Jahr 2019)

Der heutige spektrale Verlauf der Abstrahlung, d.b. bei 415 ppm $CO_2$, läßt sich mit dem Auge nicht von dem vorindustriellen mit 280 ppm unterscheiden. Die Differenzen sind bislang sehr viel geringer als die Meßgenauigkeit von Satelliten. Das heißt im Klartext, dass bis zum heutigen Tag noch niemand einen physikalisch validen Nachweis über den CO2-bedingten Treibhauseffekt erbracht hat.  Aus der Modell-Berechnung, die mit vielen expliziten und impliziten Annahmen versehen ist, ergibt sich ein um $1.66\frac{W}{m^2}$ verringerter Wärmefluß gegenüber vorindustrieller Zeit – falls es außer der CO2-Änderung seit 150 Jahren keinerlei anderweitige Veränderungen in der Atmosphäre gab ( 🙂 ). Das sind max. $0.02 \frac{W}{m^2}$ pro Jahr, was um etwa einen Faktor 400 unter der Meßgenauigkeit der Satellitendaten von $8 \frac{W}{m^2}$ pro Jahr liegt. Selbst bei einem angenommenen Beobachtungszeitraum von 20 Jahren wäre man immer noch um einen Faktor 20 unter der Meßgenauigkeit. Selbst der gesamte bisherige angenommene Treibhauseffekt wäre noch um einen Faktor 5 unterhalb der Nachweisgrenze (wenn es 1850 schon Satelliten gegeben hätte).  Auch bei der Analyse des Energiebudgets an der Erdoberfläche ist der Meßfehler um eine Größenordnung größer als die möglichen Auswirkungen des Treibhauseffekts. 

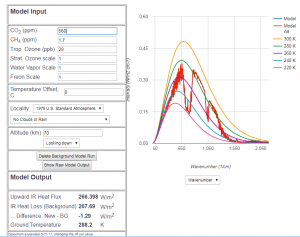
Abb 8: MODTRAN Abstrahlungsmodell für 560 ppm $CO_2$-Anteil (doppelter Wert von 1850), überlagert dem Modell mit 415 ppm

In Abb. 8 ist der künftige hypothetische Abstrahlungsverlauf mit 560 ppm $CO_2$-Anteil dem heutigen Verlauf direkt überlagert. Wieder sind die beiden Kurven nahezu identisch. Aus der Wärmefluß-Berechnung ergibt sich bei 560 ppm gegenüber heute eine Verminderung des abgestrahlten Wärmeflusses von etwa $1.3\frac{W}{m^2}$.  Obwohl die Differenz der $CO_2$-Menge größer ist als die von der Vergangenheit bis heute, ist die Auswirkung geringer. Das hat mit der logarithmischen Abhängigkeit der Wärmefluss-Abnahme vom $CO_2$ Gehalt zu tun. 

Bei der Verdoppelung des $CO_2$-Gehalts verringert sich $CO_2$-bedingt der Wärmefluß um $2.95\frac{W}{m^2} $, was einer hypothetischen Erwärmung der simplen Modellatmosphäre von insgesamt 1 Grad entspricht. Wie sich leicht mit dem interaktiven Modell nachvollziehen lässt, gilt dies bei jeder Verdoppelung des $CO_2$-Gehalts. Mit zunehmendem $CO_2$-Gehalt nimmt dessen Treibhauswirkung also ab. Dieser Zusammenhang wird von IPCC-nahen Klimaforschern nicht bestritten, wird aber merkwürdigerweise fast nur von „Klimaskeptikern“ öffentlich erwähnt. 

Diese sehr einfachen Berechnungen werden durch eine IPCC-Publikation (AR3) bestätigt. Auf S. 357 wird die $CO_2$-bedingte Änderung der Abstrahlung seit der Industrialisierung mit $1.46\frac{W}{m^2}$ angegeben, und bei Verdoppelung $3.7\frac{W}{m^2}$. (Was merkwürdig ist wegen der zu erwartenden dämpfenden Wirkung bei höherem $CO_2$ Anteil )

Abstrahlung und Temperatur-Sensitivität 

Das unmittelbare Ergebnis der MODTRAN Simulation ist Abstrahlungs-Sensitivität, seit dem Beginn der Industrialisierung  bis heute $1.66\frac{W}{m^2}$  beträgt, was mehr ist als der vom IPCC berechnete Wert von $1.46\frac{W}{m^2}$ ist — deren Wert berücksichtigt auch noch die dämpfenden Aerosole.  
Konsequenterweise verwende ich zur Beantwortung der Frage der Temperatursensitivität auch wieder die MODTRAN-Simulation mit der Fragestellung: Um wieviel ist die Basistemperatur der Erdoberfläche zu erhöhen, um mit dem heutigen $CO_2$-Gehalt die gleiche Abstrahlung zu erhalten wie zu Beginn der Industrialisierung? Für den heutigen Wert 415 ppm ergibt sich, je nach Wechselwirkung mit dem Wasserdampf ein Anstieg von 0.4-0.6 Grad.  Das ist weniger als das gängige Verständnis einer Temperaturerhöhung von 0.9-1 Grad seit dem Beginn der Industrialisierung.  Die Sensitivität bei Verdopplung beträgt nach dem MODTRAN Modell 0.75-1 Grad.
Das wirft natürlich u.a. die Frage auf, ob es nicht noch andere Faktoren außer $CO_2$ gibt, die die Temperatur beeinflussen können?  Und warum die IPCC-Modelle zu deutlich verschiedenen Ergebnissen kommen, obwohl bei der Abstrahlung die IPCC Ergebnisse noch fast gleich mit den hier ermittelten sind. Wenn die Sensitivität schlicht mit der totalen Ableitung des Stefan-Boltzmann Gesetzes berechnet wird, kommen noch kleinere Werte heraus. Diese Ergebnisse besagen, daß der Einfluß von $CO_2$ auf das Klimageschehen ein geringfügiger Effekt ist, dessen Bedeutung in der Klimadiskussion stark übertrieben wird – so gering, dass er unterhalb der bislang möglichen Meßgenauigkeit ist! Das sollte jedem vernünftigen Menschen zu denken geben. 

Es ist meine Hoffnung, dass diese Zusammenstellung der physikalischen Grundlagen ein im besten Sinne konsensfähiges Fundament darstellt, von dem aus die Klimadiskussion von allen Beteiligten wieder mit sachlichen Argumenten geführt wird.

Offene Fragen

Es ist völlig klar, dass die obigen Ausführungen noch kein vollständiges „Klimamodell“ beinhalten. Zweifellos bleiben hier noch viele Fragen offen, die in künftigen Beiträgen behandelt werden:

• Der Einfluss von Rückkopplungen zwischen $CO_2$-Gehalt und Wasserdampf bzw. Wolken, nach Auffassung der IPCC-nahen Wissenschaftler der entscheidende Aspekt — falls die Rückkopplung positiv ist. 
• der Einfluss von Aerosolen,
• die wichtige Bedeutung der Weltmeere für das Klima,
• die Bearbeitung und Bewertung anderen möglichen klimarelevanten Einflüssen wie Sonnenzyklen und magnetische Sonnenaktivität,
• die Bedeutung der kosmischen Strahlung,
• die klimatischen Auswirkung der $CO_2$-bedingten zusätzlichen Begrünung der Erde,
• die Berücksichtigung der Klimazonen durch regionale Modelle

Zusammenfassung

Trotz dieser Einschränkungen gibt es bedeutende Konsequenzen aus diesen Überlegungen. Der überwiegende Anteil des sog. „Treibhauseffekts“, der die Erde durchschnittlich um 33 Grad erwärmt, hat nichts mit Treibhausgasen zu tun, sondern mit der Gesamtmasse der Atmosphäre: Je dicker eine Decke ist, mit der Sie sich zudecken, desto besser hält sie die Wärme. Die Treibhausgase Wasser und $CO_2$ spielen in erster Linie die Rolle eines Katalysators, um Strahlung durch Absorption und Stöße in eine erwärmte Atmosphäre umzuwandeln und in hinreichender Nähe zum Weltraum oder zur Erdoberfläche auch wieder abzugeben. Ein anderes Bild für die Treibhausgase ist das eines (wellenlängenabhängigen) Ventils, das Wärme in die Atmosphäre hinein- bzw. herausläßt, unter Berücksichtigung der universell gültigen physikalischen Gesetze, insbsondere der Thermodynamik. Im Inneren der Atmosphäre spielen Strahlungseffekte eine untergeordnete Rolle, dominierend ist der thermodynamische Temperaturgradient.
Der spezifische Anteil zum Treibhauseffekt durch $CO_2$ kann, abhängig von der Umgebung, positiv (fast überall) oder negativ (an den Polen) sein. Die Größe des Einflusses bei Veränderungen von $CO_2$ ist allerdings so gering, dass bei den Abstrahlungsspektren selbst bei Verdoppelung des $CO_2$ Anteils augenscheinlich kein Unterschied festzustellen ist. Dazu kommt, dass die Sensibilität gegenüber $CO_2$ mit wachsendem $CO_2$ Anteil abnimmt — die Änderung von 280 ppm auf 415 ppm hatte etwa denselben Effekt wie die von 415 ppm auf 560 ppm. Der Effekt bei Verdoppelung ohne Berücksichtigung anderer Einflußfaktoren ist mit maximal $3\frac{W}{m^2}$ in der Größenordnung von 1% der Gesamtabstrahlung und daher als geringfügig zu betrachten. Eigene Abschätzungen legen sogar einen deutlich geringeren von $1\frac{W}{m^2}$ nahe. Daraus ergibt sich — ohne Berücksichtung anderer Effekte wie Wolkenalbedo oder Energiespeicherung im Klimasystem — eine Klimasensitivität von etwa 0.5-1 Grad.

Die Rückkopplungseffekte durch Wasserdampf und Wolken werden gesondert diskutiert, die Vereinfachung, diese hier zu vernachlässigen, ist durch wissenschaftliche Untersuchungen gerechtfertigt, dass die Klimamodelle, die positive Rückkopplungen beinhalten, die gemessenen globalen Temperaturen der letzten 20 Jahre systematisch überschätzen.

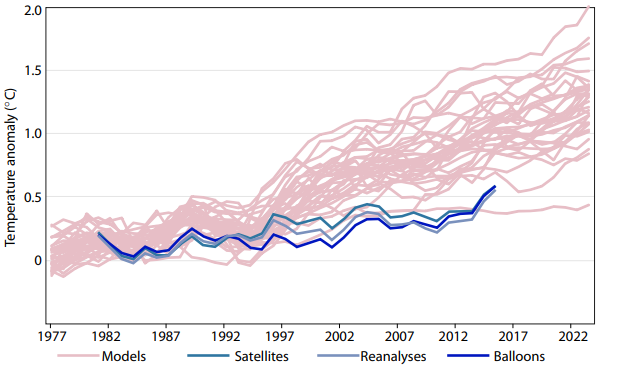
Dies ist keine einseitige Einzelmeinung. Mehrere seriöse Wissenschaftler kommen zu dem Schluss, den jeder Laie bei Betrachtung der tatsächlichen Temperaturentwicklung und der Modellprognosen nachvollziehen kann, dass nämlich alle Modelle mit Rückkopplung deutlich höhere Temperaturen als tatsächlich gemessen prognostizieren:

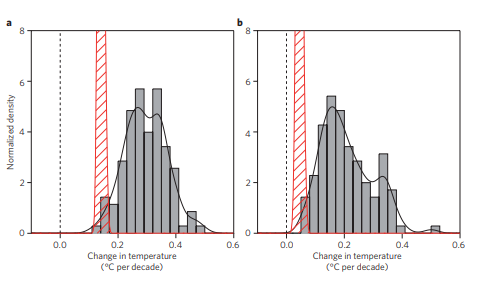
Das einfache Modell mit reinem CO₂ Antrieb ohne positive Rückkopplung passt viel besser zu den Daten zwischen 1980 und heute. Dies rechtfertigt die Modellannahme, dass es keinen verstärkenden Rückkopplungseffekt gibt und dass der $CO_2$ bedingte Temperaturanstieg bis zum Ende des Jahrhunderts 1.1 Grad C nicht überschreiten wird.