Water Vapour Feedback
[latexpage]
In the climate debate, the argument of feedback through water vapor is used to amplify the climate effect of greenhouse gases – the sensitivity to a doubling of their concentration in the atmosphere – which, according to the radiative transfer equation and general consensus, is a maximum of 0.8°, by an alleged factor of 2-6. However, this is usually not quantified more precisely, only formulas with the „final feedback“ are usually given.
Recently, David Coe, Walter Fabinski and Gerhard Wiegleb described and analyzed precisely this feedback in the publication „The Impact of CO2, H2O and Other ‚Greenhouse Gases‘ on Equilibrium Earth Temperatures„. Based on her publication, this effect is derived below using partly the same and partly slightly different approaches. The results are almost identical.
All other effects that occur during the formation of water vapor, such as cloud formation, are ignored here.
The basic mechanism of water vapor feedback
The starting point is an increase in atmospheric temperature by ∆T0, regardless of the cause. Typically, the greenhouse effect is assumed to be the primary cause. The argument is now that the warmed atmosphere can absorb more water vapor, i.e. the saturation vapor pressure (SVP) increases and it is assumed that consequently the water vapor concentration ∆H2O also increases, as a linear function of the temperature change. (The temperature change is so small that linearization is legitimate in any case):
$\Delta H_2O = j\cdot \Delta T_0 $
where $j$ is the proportionality constant for the water vapor concentration.
An increased water vapor concentration in turn causes a temperature increase due to the greenhouse effect of water vapor, which is linearly dependent on the water vapor concentration:
$\Delta T_1 = k\cdot \Delta H_2O $
In summary, the triggering temperature increase ∆T0 causes a subsequent increase in temperature ∆T1:
$\Delta T_1 = j\cdot k\cdot \Delta T_0 $
Since the prerequisite of the method is that the cause of the triggering temperature increase is insignificant, the increase by ∆T1 naturally also causes a feedback cycle again:
$\Delta T_2 = j\cdot k\cdot \Delta T_1 = (j\cdot k)^2\cdot \Delta T_0$
This is repeated recursively. The final temperature change is therefore a geometric series:
$\Delta T = \Delta T_0\sum_{n=0}^\infty(j\cdot k)^n = \Delta T_0\cdot \frac{1}{1-j\cdot k} $
If $j\cdot k\ge 1$, the series would diverge and the temperature would grow beyond all limits. It is therefore important to be clear about the magnitude of these two feedback factors.
For the determination of the first term, $j$ we can apply a simplified approach by accepting the statement commonly used in the mainstream literature, that for each degree C of temperature increase the relative air moisture may rise up to 7%. In the German version of this post I did the explicit calculations and came to the result that the realistic maximum air moisture rise is 6% per degree temperature rise, which has hardly any effect on the final result.
Dependence of the greenhouse effect on the change in relative humidity
Infrared radiation transport in the atmosphere is dependent on relative humidity. This is taken into account in the well-known and proven MODTRAN simulation program. With increasing humidity, the outgoing infrared radiation decreases due to the greenhouse effect of water vapor.
The decrease in radiation is linear between 60% and 100% humidity. Therefore, the increase in relative humidity from 80% to 86% is considered to determine the decrease in radiant power and the temperature increase required for compensation.
To do this, we set the parameters of the MODTRAN simulation to
- the current CO2 concentration of 420 ppm,
- a relative humidity of 80%,
- and a cloud constellation that comes close to the average IR radiant power of 240 $\frac{W}{m^2}$.
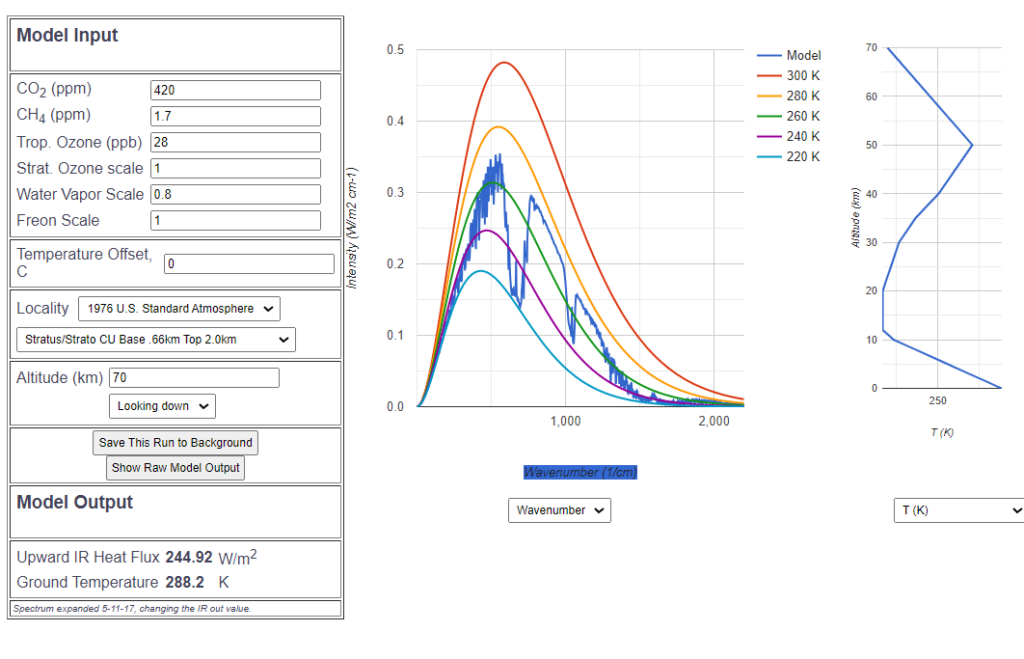
The temperature offset is now increased until the reduced iR radiation of 0.7 \frac{W}{m^2} is compensated for by increasing the temperature. This is the case when the ground temperature is increased by 0.215 °C.
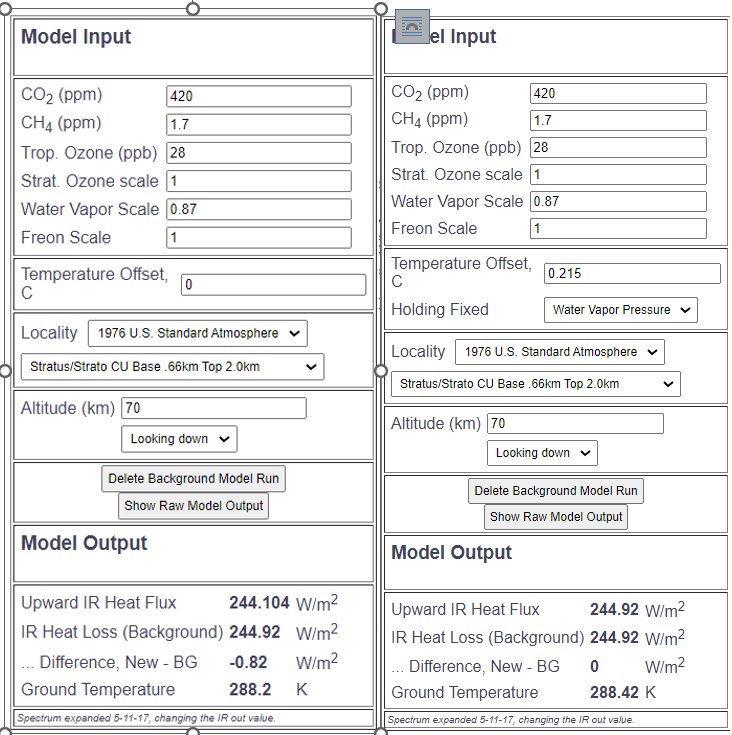
A 7% higher relative humidity therefore causes a greenhouse effect, which is offset by a temperature increase of 0.215°C. Extrapolated to a (theoretical) change of 100% humidity, this results in $k=3.07$°C/100%.
The final feedback factor and the total greenhouse effect
This means that a 1 degree higher temperature in a feedback cycle causes an additional temperature increase of $k\cdot j = 0.215$.
The geometric series leads to an amplification factor $f$ of the pure CO$_2$ greenhouse effect by
$f=\frac{1}{1-0.215} = 1.27 $
This means that the sensitivity amplified by the water vapor feedback when doubling the CO$_2$ concentration $\Delta T$ is no longer $\Delta T_0=0.8$°C, but
$\Delta T = 1.27\cdot 0.8$ °C = 1.02°C $\approx$ 1°C
This result does not take into account the increase in temperature caused by the higher water vapor concentration