Lässt die Wirkung der Senken nach oder nicht?
[latexpage]
Einleitung — was sind Senken?
Zunächst wird die messbare Senkenwirkung $S_i$ des Jahres $i$ als Bilanzgleichung aufgrund der Erhaltung der Gesamtmasse des CO2 und der Kontinuitätsgleichung bestimmt. Der Konzentrationszuwachs $G_i$ der Atmosphäre ergibt sich als Differenz aller Emissionen, also sowohl der anthropogenen Emissionen $E_i$ und der natürlichen Emissionen $N_I$, und der gesamten Absorptionen $A_i$:
$G_i= C_i – C_{i-1} = E_i + N_i – A_i$ (1)
Die Senkenwirkung $S_i$ ist der Anteil der anthropogenen Emissionen $E_i$, die nicht zum Anwachsen der Konzentration $G_i$ beitragen:
$S_i = E_i – G_i$ (2)
Diese Senkenwirkung ist aus den verfügbaren Emissions- und CO2-Konzentrations-Daten ohne Modellierung leicht ermittelbar und in Abbildung 1 als Zeitserie ab 1960 gezeigt. Die Daten des monatlich gemessenen Konzentrationszuwachses sind desaisonalisiert, indem jeweils die Differenz zum gleichen Vorjahresmonat bestimmt wird. Emissionen und Konzentration sind in der gleichen Maßeinheit ppm gemessen (1 ppm = 2,123 Gt C = 7,8 Gt CO2)
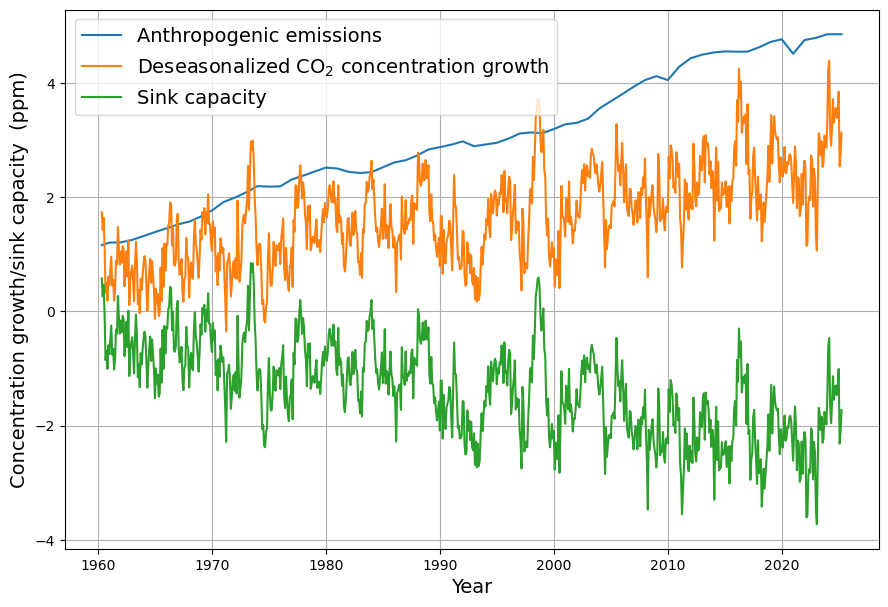
Demzufolge ist die Senkenwirkung auch die Differenz zwischen Absorptionen $A_i$ und natürlichen Emissionen $N_i$
$S_i = A_i -N_i $ (3)
Daraus folgt auch, dass die — mit großen Unsicherheiten behafteten — Emissionen durch Landnutzungsänderungen zunächst als zu den unbekannten natürlichen Emissionen gehörig gerechnet werden.
Da die globale Senkenwirkung die einzige Kenngröße ist, die einer einfachen Messung zugänglich ist, muss eine Methode gefunden werden, um mit der gemessenen Senkenwirkung das Senkenmodell zu bewerten. Ziel dieser Untersuchung ist nicht, die Korrektheit der jeweiligen Modelle aus inhaltlichen Gründen zu bewerten, sondern einzig und allein, ein Kriterium zu finden, um aufgrund von Messdaten zu entscheiden, welche Modellklasse besser mit der Realität übereinstimmt.
Die beiden Senkenmodelle
Das lineare Senkenmodell
Es werden 2 Senkenmodelle gegenübergestellt. Das eine, das „lineare Senkenmodell“ oder auch „Badewannenmodell“ geht davon aus, dass die Senkenwirkung im Jahre $i$, $S_i$ streng linear mit der CO₂-Konzentration (des Vorjahrs) $C_{i-1}$ anwächst:
$S_i = a\cdot C_{i-1} + b = a\cdot(C_{i-1} – C^0)$ (4)
wobei $C^0=-b/a$ die angenommene präindustrielle Gleichgewichtskonzentration ohne anthropogene Emissionen darstellt.
Aus den Daten des Zeitraums 1960-2025 ergeben sich diese Schätzwerte:
$a=0,0174, b=-4,87, C^0 =280 $ ppm
Der Schätzwert der Gleichgewichtskonzentration $C^0$ stimmt bemerkenswert gut mit der angenommenen präindustriellen Gleichgewichtskonzentration überein.
Bei der Modellgleichung handelt es sich um eine Differenzialgleichung 1. Ordnung mit der Impulsantwort
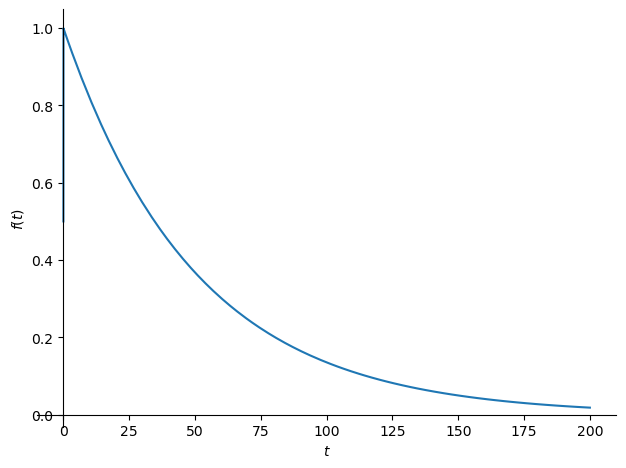
$IRF^{linear}(t)=e^{-\frac{t}{\tau}}$
mit $\tau=1/a\approx 57 $ Jahre.
Entscheidend ist, dass die Impulsantwort vollständig auf 0 abklingt, was bedeutet, dass das atmosphärische CO₂ mit der Zeit vollständig von den Senken absorbiert wird.
Das Berner Modell
Um nicht voreilig falsche Schlussfolgerungen aus dem Berner Modell zu ziehen, erscheint es wichtig, zunächst einen Vorläufer des Berner Modells zu betrachten, das sogenannte 2-Boxen-Modell. Ausgangspunkt des 2-Boxen-Modells ist die im Prinzip richtige Überlegung, dass auch die CO₂-Senken, die Ozeane und die Landpflanzen, endlich sind und nur eine begrenzte Menge an CO₂ aufnehmen können. Das einfachste Modell, das diesen Umstand berücksichtigt, ist das 2-Boxen-Modell, wonach die Atmosphäre die eine Box darstellt, die Ozeane zusammen mit den Landpflanzen die 2. Box.
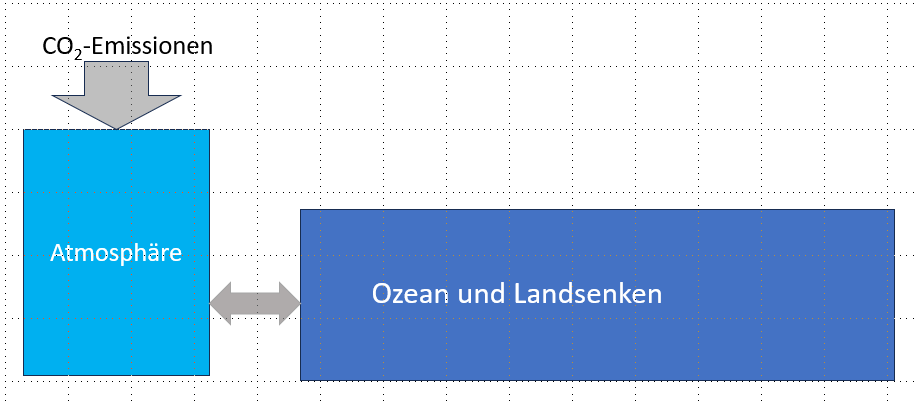
Diese 2. Box ist um den Faktor $p$ größer als die erste Box. Um den Effekt zu verdeutlichen, wird $p=3$ angenommen. Es erscheint extrem, dass die Ozeane und die Landpflanzen zusammen nur 3-mal größer angenommen werden als die Atmosphäre. Aber das ist tatsächlich der Wert, von dem die aktuelle Klimaforschung (z.B. Prof. Marotzke) ausgeht, obwohl bekannt ist, dass alleine die Ozeane insgesamt etwa 50-mal so viel CO₂ gebunden haben wie die Atmosphäre. Beim Berner Modell ist der Faktor $p$ eher bei 4. Wenn man sich vorstellt, dass der aufnehmende Container tatsächlich nur 3-mal größer ist als die Atmosphäre, dann ist auch klar, dass von jedem zusätzlichen CO₂-Eintrag in die Atmosphäre am Ende, d.h. im Gleichgewichtszustand, 25% in der Atmosphäre zurückbleiben, und nur 75% von den Senken aufgenommen werden können. Dies wird mit der Impulsantwort verdeutlicht.
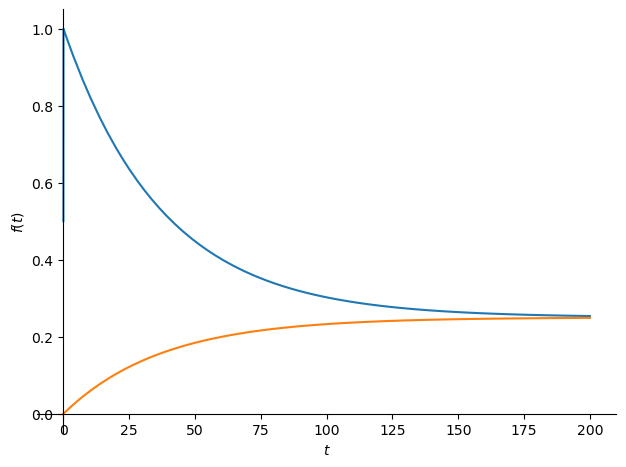
Das Berner Modell ist ein 4-Boxen-Modell. Es unterteilt den Ozean in 2 Teile. Während in dem oberen Teil der Gasaustausch mit einer ähnlichen Zeitkonstante wie beim linearen Modell geschieht (da dafür nur die oberste Schicht „Mixed Layer“ berücksichtigt wird, ist der Austausch noch schneller als beim linearen Modell) , geschieht der Fluss in die Tiefsee durch eine sehr langsame Diffusion. Die 4. Box repräsentiert die Landpflanzen. Dadurch, dass die Tiefsee durch den langsamen Diffusionsprozess für Hunderte von Jahren „abgeschirmt“ ist, erklärt sich die vermeintlich kleine „Ozean-Box“ und der daher große konstante Rest von über 20% in der Atmosphäre.
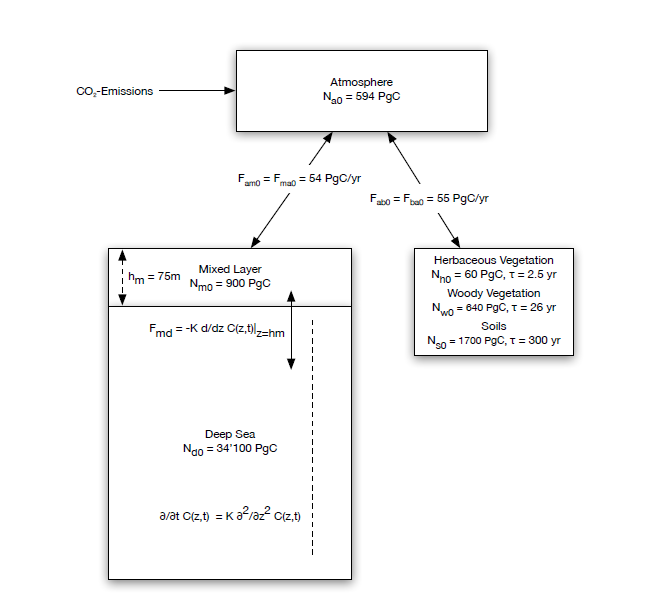
einfachem globalen Kohlenstoffmodell“, Prof. Martin Heimann, April 2024 bei 4Pi-Solutions)
Die publizierte Näherungsgleichung des Bern-Modells ist
$ IRF^{Bern}(t) =a_0 + \sum_{i=1}^3 a_i\cdot e^{-\frac{t}{\tau_i}}$ (5)
mit a0=0.21787, a1=0.22896, a2=0.28454, a3=0.26863, tau1=381.33, tau2=34.785, tau3=4.1237
Die mathematische Form der Näherungslösung und die zitierte Publikation suggerieren, dass es sich um 4 parallele Prozesse handelt. Das ist aber nicht so, es ist nur eine Näherungslösung eines komplexen 4-Boxen-Prozesses, damit den Prozess einfacher als gewichtete Summe linearer Prozesse formulieren zu können.
Abb. 6 zeigt die Impulsantworten (IRF) des Bern-Modells (grün) im Vergleich zum obigen linearen Modell (blau) und zum 2-Boxen-Modell (orange).
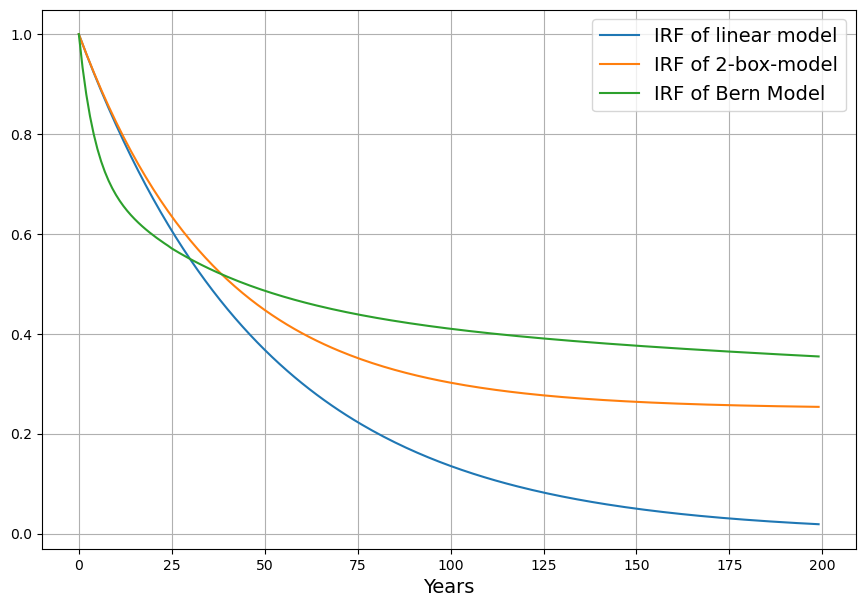
Während zu Beginn der Konzentrationsabfall des Berner Modells stärker ist als beim linearen Modell, wird der Verlauf bald flacher, sodass nach 100 Jahren nur 60% absorbiert sind, beim linearen Modell sind es da bereits 85%. Das 2-Boxen-Modell liegt vom Verlauf her zwischen dem linearen und dem Berner Modell, langfristig geht es ähnlich wie das Berner Modell in die Sättigung, d.h. es bleibt ein substantieller Teil des CO₂ in der Atmosphäre.
Anwendung auf realitätsnahen künstlichen Emissionsverlauf
Wie oben beschrieben, ist die gemessene Senkenwirkung die Schnittstelle zwischen Modell und Wirklichkeit. Vor der Anwendung auf die tatsächlichen Messdaten wird die geplante Vorgehensweise mit einem künstlichen einfachen Emissionsverlauf simuliert, der qualitativ dem tatsächlichen Verlauf ähnlich ist. Der Vorteil eines wohldefinierten Emissionsverlaufs ist, dass die Modellunterschiede klar herausgearbeitet werden können, ohne von Rauscheffekten und anderen unbekannten Einflüssen beeinflusst zu sein. Außerdem wird nicht zwischen gemessenen Emissionen der Vergangenheit und projizierten Emissionen der Zukunft unterschieden. Die simulierten Emissionen wachsen ab 1920 für 100 Jahre linear auf 5 ppm/Jahr an und bleiben von da an konstant (Abb 7):
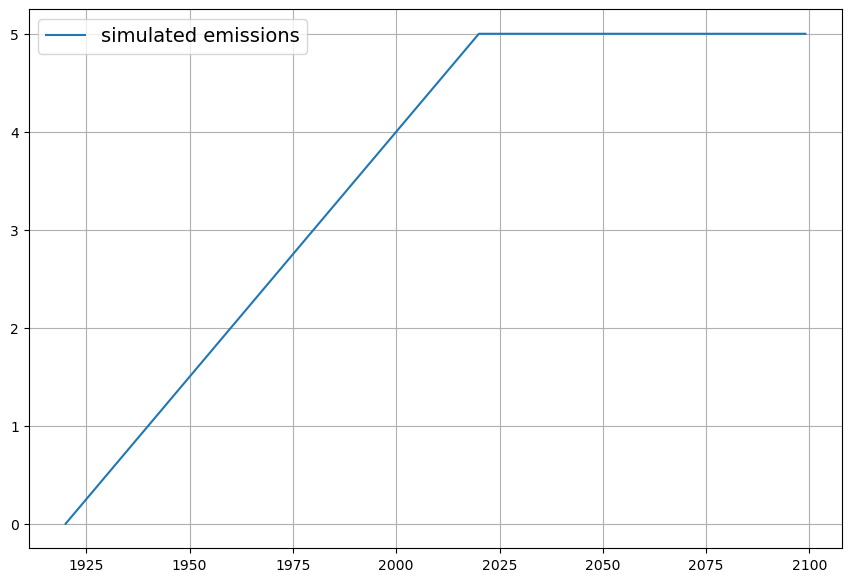
Durch Faltungen mit den jeweiligen Impulsantworten ergeben sich die Konzentrationsverläufe der beiden Modelle und einer natürlichen Gleichgewichtskonzentration von 280 ppm (Abb. 8):
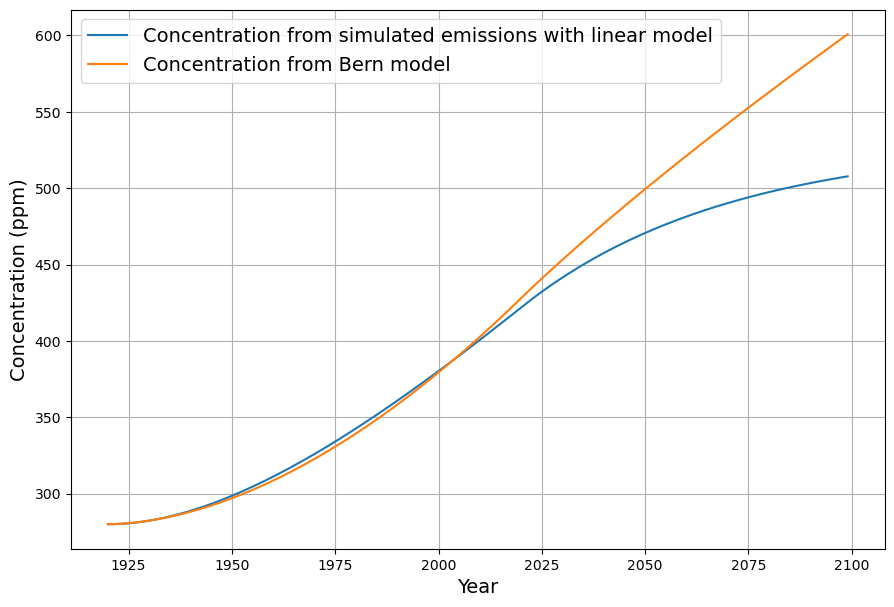
Es ist aus Abb. 8 deutlich erkennbar, dass die Senkenwirkung des Berner Modells im Vergleich zum linearen Modell auf lange Sicht deutlich nachläßt. Durch Differenzbildung jeweils benachbarter Datenpunkte wird das Konzentrationswachstum bestimmt (Gleichung (1)). Die für das Unterscheidungskriterium wichtige gemessene Senkenwirkung wird dann aus der Differenz zwischen Emissionen und Konzentrationswachstum nach Gleichung (2) bestimmt. Alle Daten sind in Abbildung 8 zusammengefasst.
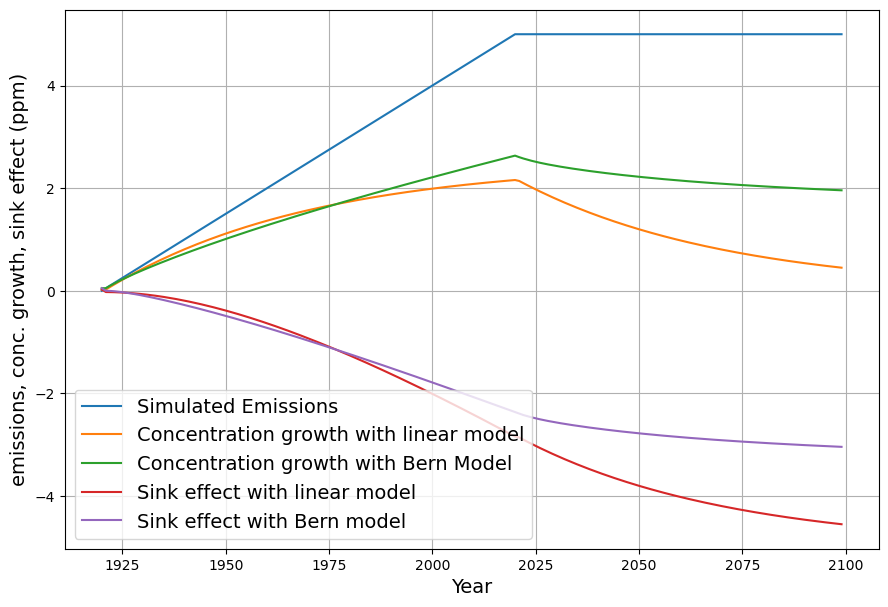
Es wird zur Unterscheidung ein Kriterium benötigt, mit dem man beurteilen kann, ob ein Senkenverlauf „flacher“ als der Verlauf des linearen Modells ist.
Kriterium zur Unterscheidung des linearen Modells von den „abflachenden“ Modellen
Um über die Gültigkeit der Modellklasse zu entscheiden, wird ein Kriterium benötigt, um mit Hilfe eines statistisch bestimmbaren Paramenters eine Aussage über die Modellklasse zu machen. Dazu wird Gleichung (4) etwas verallgemeinert, indem die von der Gleichgewichtskonzentration abweichende Konzentration mit $p$ potenziert wird:
$S_i = a\cdot(C_{i-1} – C^0)^p$
Um $p$ aus gegebenen Daten zu bestimmen, wird die Gleichung logarithmiert:
$ln(S_i) = ln(a) + p\cdot ln(C_{i-1} – C^0)$ (6)
Mit $p=1$ ist die Gleichung identisch mit dem linearen Senkenmodell. Mit $p<1$ bekommt man einen flacheren Verlauf. Wenn nun nachweisbar ist, dass $p$ signifikant kleiner als 1 ist, dann wäre das ein Beweis für ein langfristiges Nachlassen der Senkenwirkung. Umgekehrt: Wenn das Berner Modell korrekt ist, muss der Abflachungseffekt bereits heute erkennbar sein.
Zunächst wollen wir anhand der künstlichen Daten überprüfen, welche Werte von $p$ aufgrund der Modellannahmen zu erwarten sind. Dabei wird die Schätzung nicht über den gesamten Datenbereich durchgeführt, sondern nur über die 70 Jahre 1950-2020, den gleichen Zeitraum, der auch bei den realen Daten relevant ist.
Für das lineare Modell ergibt die Least-Squares Schätzung mit Gleichung (6):
Variable Schätzwert Std. Fehler t-Wert Fehler-WS 95% Vertrauens-Intervall
p 0.9858 0.0006 1584.8340 0.0000 [ 0.9846 0.9870]
ln(a) -3.8447 0.0026 -1474.3731 0.0000 [-3.8499 -3.8395]
Der Exponent p ist mit 0,99 sehr nahe bei dem Wert 1 des linearen Modells. Das ist nicht verwunderlich, da die Daten mit dem linearen Model konstruiert wurden.
Beim der Schätzung von Gleichung (6) der mit dem Bern-Modell konstruierten Daten ergeben sich diese Werte:
Variable Schätzwert Std. Fehler t-Wert Fehler-WS 95% Vertrauens-Intervall
----------------------------------------------------------------------------------------
p 0.7256 0.0009 790.5613 0.0000 [ 0.7237 0.7274]
ln(a) -2.7563 0.0038 -722.0434 0.0000 [-2.7639 -2.7487]
Mit den idealtypischen Daten des Berner Modells erhalten wir bei gleichmäßiger Steigerung der Emissionsdaten demnach für $p$ eine große Abweichung von 1.
Test mit den realen Messdaten
Der entscheidende Test erfolgt mit den echten gemessenen Daten. Mit den Zeitreihen bis Ende 2024 sind die Unterschiede der Modelle bei der Rekonstruktion der gemessenen CO2-Konzentration sehr gering (Da die Messdaten vor 1960 ohnehin unzuverlässig sind, sind die Abweichungen vor 1960 von untergeordnetem Interesse).
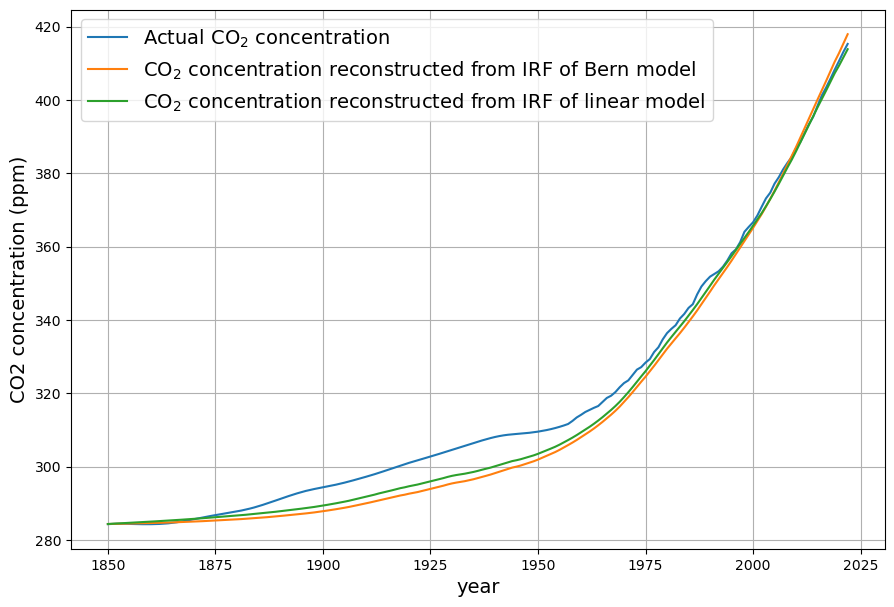
Deswegen werden die aussagekräftigeren Verläufe des Konzentrationswachstums und des gemessenen Senkeneffekts betrachtet. Da sind in der Tat bereits heute leichte Unterschiede erkennbar. Diese sind aber — als Einzelwerte — immer noch innerhalb der großen statistischen Schwankungen.
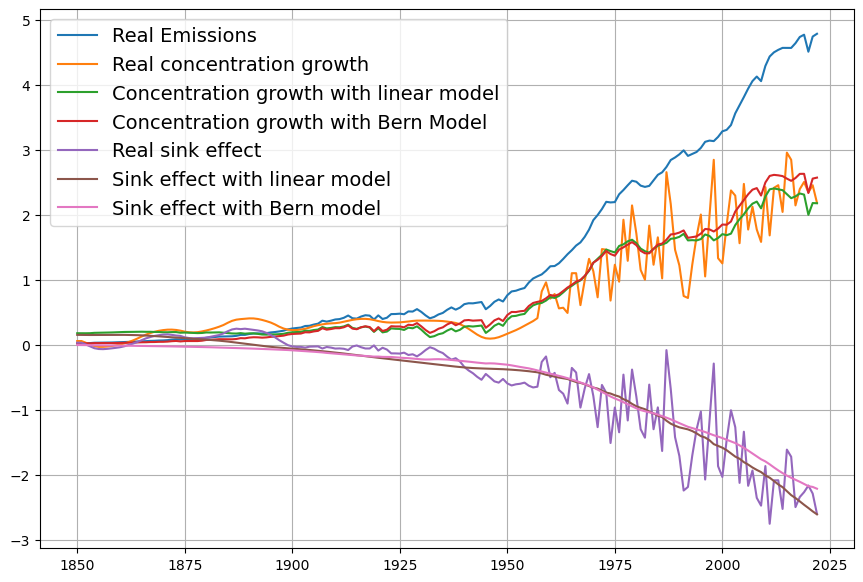
Aber es ist ein Trendunterschied erkennbar.
Um den Trend mit dem neuen Werkzeug messen zu können, ist eine Bestimmung der Gleichgewichtskonzentration $C^0$ erforderlich, denn von dieser hängt das Schätzergebnis maßgeblich ab.
Für das Bern Modell die richtige „Gleichgewichtskonzentration“ zu bestimmen, ist nicht ganz trivial, denn das Berner Modell kennt keine Gleichgewichtskonzentration — nach diesem Modell wird die atmosphärische Konzentration nie wieder zum präindustriellen „Gleichgewicht“ zurückkehren. Es geht aber darum, den Verlauf der letzten 70 Jahre mit einem veränderten linearen Verlauf zu vergleichen. Aus dem Modellierungsverlauf der Senkenwirkung in Abb. 10 ist erkennbar, dass das lineare und das Berner Modell im Zeitraum 1950-1990 fast identisch sind. Daher ist es sinnvoll, für die Bestimmung der Gleichgewichts-Konzentration diesen Zeitraum von 40 Jahren herzunehmen. Damit erhält man aus den realen Daten eine Gleichgewichtskonzentration $C^0=282$ ppm. Wendet man nun die Gleichung 6 auf die Senkeneffektdaten des Berner Modells an (Abb. 10, pink Kurve) mit den Konzentrationsdaten des Berner Modells als Prädiktor (Abb. 9, orange Kurve).
Variable Schätzwert Std. Fehler t-Wert Fehler-WS 95% Vertrauens-Intervall
--------------------------------------------------------------------
p 0.9192 0.0092 100.2195 0.0000 [ 0.9009 0.9375 ]
ln(a) -3.6269 0.0360 -100.6758 0.0000 [-3.6987 -3.5550 ]
Der Verlauf des Berner Modells impliziert mit $p=0,9$ eine klare Abweichung vom linearen Modell in Form der zurückgehenden Senkenwirkung.
Beim linearen Modell, das wir für die 70 Jahre 1950-2020 schätzen, ergibt sich die Gleichgewichtskonzentration von selbst nach Anwendung von Gleichung (4). Diese beträgt in diesem Falle etwa 283 ppm. Daraus folgt dann nach Gleichung (6)
Variable Schätzwert Std. Fehler t-Wert Fehler-WS 95% Vertrauens-Intervall
-------------------------------------------------------------------
p 1.0100 0.1308 7.7223 0.0000 [ 0.7490 1.2710 ]
ln(a) -4.0994 0.5351 -7.6612 0.0000 [-5.1671 -3.0316 ]
Demnach ist ergibt sich eine perfekte Bestätigung des linearen Modells mit $p=1$. Demnach sind Modelle, die vom streng linearen Zusammenhang zwischen Konzentration und Senkeneffekt statistisch wenig wahrscheinlich. Aus wissenschaftstheoretischer Sicht muß man sich fragen, warum ein Modell mit 7 freien Parametern (Berner Modell) einem Modell mit einem freien Parameter (lineares Senkenmodell) vorzuziehen ist, wenn die Meßdaten mit mindesten 70-90% Sicherheit das Modell mit den vielen Parametern ausschließen.
Diese Überlegungen sind die ersten, vereinfachten Überlegungen zu dieser Thematik. Mit verfeinerter Verarbeitung der Daten, wie z.B. unter Nutzung höherer Auflösung, lässt sich die Signifikanz der Aussagen deutlich verbessern. Das erfordert allerdings eine umfangreiche Behandlung des damit verbundenen komplexeren Modells. Mit Aktualisierungen dieser Seite ist zu rechnen.