Lapse Rate made simple

Atmospheric temperature varies with height. This well known and well understood phenomenon is called lapse rate. It describes the altitudinal temperature gradient, essentially stating that temperature decreases by 4-9.8 degrees C per km elevation. The reason for discussing this here is, that temperature changes are often incorrectly attributed to a radiative “greenhouse effect”, where in fact they are the thermodynamic consequence of a gas volume in a gravitational field.
There are many ways to explain this phenomenon. Here I want to do it in the most elementary way.

The first important assumption is the local thermodynamic equilibrium. It means that in a certain volume of air there are no macroscopic state changes of e.g. temperature or pressure. Let us assume a volume of air that is large enough so that temperature can be defined, and that is small enough so that the temperature is constant in that volume, typically called “parcel of gas”.
This volume with mass is in the planetary gravitational field with gravitation constant . At height h it has the potential energy

   

and the thermal energy of this volume with heat capacity (at constant pressure) and temperature w.r.t. reference temperature is

   

The second assumption is that the system is adiabatic, i.e. there is no energy flowing into or out of the system. This means, that the sum of and is constant:

   

Therefore the total derivative of E must be 0:

   

   

From this the temperature gradient, i.e. lapse rate, follows directly:

   

What does this mean? Starting from the assumption of local conservation of energy, a molecule moving upwards loses motion energy in exchange for potential energy, must therefore get cooler by the corresponding energy amount, in other words raising a mass in the gravitational field must be paid from the motion energy, and a falling mass is accelerated, raising the temperature. Equilibrium is reached when the entropy of the system is maximal.
With and the adiabatic lapse rate for dry air is

   

If the air is humid, depending on pressure and temperature, water vapor condenses to liquid water, releasing the latent heat of 2260 J/g. This additional condensation energy reduces the lapse rate, because the “price” for potential energy can (partially) be paid from the condensation energy without decrease of temperature. The resulting moist adiabatic lapse rate is in the range -4…-9.8 K/km, depending on the humidity of the air. The global average lapse rate is -6.4 K/km.
For diving deeper into this and other details, here is an exhaustive discussion of atmospheric physics.

What has lapse rate to do with climate or greenhouse effect? In fact lapse rate explains much if not all global temperature difference between the surface of the earth and the top of troposphere withouth explicit assumptions about “forcing” or greenhouse gases (greenhouse gases are, however, relevant for the interaction with infrared radiation). The state described by lapse rate is an equilibrium state of the atmosphere without flow of energy:

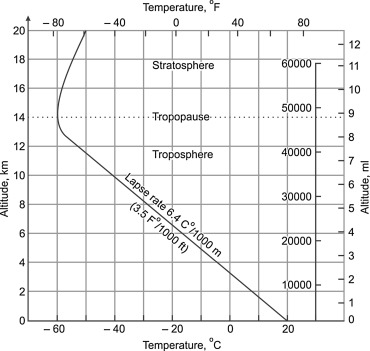
If the atmosphere deviates from this state, thermodynamics strongly forces the system towards it, in the same way as a gas distributed inside a container tends towards the state of equal density.
Lapse rate (temperature gradient) is strongly correlated to a pressure gradient by the adiabatic barometric equations. Therefore sometimes the notion is used that “pressure causes temperature”. In the context of adiabatic conditions in a gravitational field this is not wrong. It must be stated, however, that high pressure alone is not sufficient for high temperature – gas containers with very high pressure can be very cold. Therefore I prefer to refer to first principles such as energy conservation and entropy maximisation to describe the phenomenon.

The concept of lapse rate is very powerful in atmospheric science: In 1967 the surface temperature of Venus was determined correctly by evaluating the lapse rate – no explicit reference to greenhouse gases was required, although it is obvious, that the infrared radiation into space comes from the greenhouse gases close to the top of the atmosphere. This has recently been re-calculated with improved heat capacity parametrization.