IR re-emission demythologized

[latexpage]

IR re-emission – the traditional explanation

The communicated common understanding of the greenhouse effect depends very much on the re-emission hypothesis: Molecules of greenhouse gases such as $CO_2$ absorb infrared radiation, typically in the absorption band with the wavelength around $16 \mu m$, reaching an excited state. After some time the molecules return to the „ground state“, thereby emitting infrared radiation of the same wavelength isotropically. This is typically interpreted as radiating 50% upwards, and 50% downwards. Due to the assumption that all $CO_2$ molecules do this, it is imagined that approximately half of the upwelling IR surface radiation is radiated back to the surface, resulting in „downwelling“ IR. As this is additional heat reaching the surface, the surface is heated up. This is being called the „greenhouse effect“. Understandably the more $CO_2$ there is in the atmosphere, the more it heats up.
With such a simple picture it is understandable that many claim that „the science is settled“.

Radiation is converted to thermal motion

A necessary condition for the behaviour described above to work, would be that the atmosphere was so thin that the probability for the decay of an excited $CO_2$-state is higher than the probability to collide with another gas molecule. In the real atmosphere, specifically the troposphere, the process is different. Let’s assume that $CO_2$ molecules of the atmosphere are excited by infrared radiation (IR). This diagram shows,

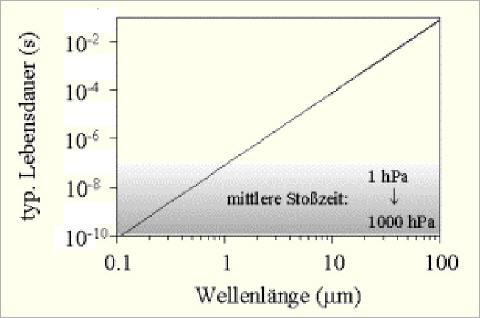
that the lifetime of an excited $CO_2$-molecule for wavelength $16\mu m$ is appr. $10^{-4}$s. But the time between collisions with neighboring molecules is between $10^{-10}$ s and $10^{-8}$ s, depending on air pressure. Therefore the probability to transfer energy by collision is 10000-1000000 times larger than by re-emission. Additionally, the probablity to collide with a non-$CO_2$ molecule is $99.96$%.
Collisions are described by thermodynamics. From gas law and energy conservation in the thermodynamic equlibrium this results in a state distribution described by the adiabatic barometric equations, essentially stating, that in an atmosphere subject to a gravitational field both density as well as temperature decrease with height above the surface. The temperature gradient is commonly called lapse rate. It is important to note that this temperature gradient is entirely caused by thermodynamics – it is the state of maximum entropy of a gas in a gravitational field, it has nothing to do with radiative forcing. For dry air the (dry adiabatic) lapse rate is $\Gamma_d = \frac{dT}{dz} = – \frac{g}{c_p} = – 9.8 C/km$, only dependent on the gravitation constant and the specific heat, the moist adiabatic lapse rate includes the condensation heat of water vapor, and is in the range of $\Gamma_m = 4-9.8 C/km$, depending on the water vapor concentration.
Whereever heat is introduced into the atmosphere, it is forced to distribute thermodynamically across the whole atmosphere, with the equilibrium state of a temperature distribution according to the moisture dependent lapse rate. The so-called standard atmosphere has a lapse rate of $\Gamma = -6.4 C/km$, which is approximately the measured global average lapse rate. This „thermodynamic forcing“ is so overwhelmingly dominant (89%), that any other effects like radiative forcing are of minor significance within the troposphere. In the tropopause and above it is different. The atmosphere is so thin, that there is no thermodynamic equilibrium, and consequently the radiation effects dominate there.

Thermal motion is converted to radiation

Obviously the process also works in the other direction. A $CO_2$ molecule may get excited by collisions and then radiates. But from the numbers above it is fairly clear, that direct re-emission plays a neglegible role in the interior of the troposphere: Any excited greenhouse gas molecule is overwhelmingly likely to distribute its additional energy to its neighbor molecules by collisions, the result is a local state of thermodynamic equilibrium. This is usually called „thermalisation“ (interestingly Wikipedia does not mention atmospheric processes – honi soit qui mal y pense) . Therefore any selected volume sufficiently large to have a thermodynamic equilibrium can be regarded as an independent Planckian emitter of (infrared) radiation. So it is possible that a volume absorbing IR with $CO_2$ is later emitting IR of another wavelength from water vapor (and vice versa). Thermodynamics permanently re-arranges the gas volume towards the local thermodynamic equilibrium. Any absorbed energy is locally quickly distributed across all neighboring molecules , some of which can radiate IR, and most others can’t. From such a volume you get a Planck emission spectrum involving all local greenhouse gases, not only $CO_2$.
Re-emission can therefore not be defined on a single molecule but emissions are independent of absorptions and are defined on a large enough volume to have a thermodynamic equilibrium.

Downwelling radiation and heat transport

According to Planck’s law a volume with higher temperature emits more radiation at all wavelengths. Volumes from higher altitudes emit less radiation because of temperature and densitiy gradients. Therefore upwelling radiation is always larger than downwelling radiation, with the important consequence that – under the condition of a lapse rate – there is no radiative heat transport from higher altitude to lower altitude. This is in accord with the 2nd law of thermodynamics, according to which heat can never flow spontaneously from a colder system to a warmer system.

Radiation at the boundary of the atmosphere

As soon as we are „close enough“ to space, i.e. within 1 optical depth (which is wavelength dependent), then actual emission into space becomes possible, and takes place, because there are not enough suitable molecules above to absorb all radiation .  Water vapor is by far the most relevant absorbing and emitting gas. Fig. 3 shows that there is a sharp drop of water vapor density at about 5 km altitude.

Radiative equilibrium at top of atmosphere

Whereas all energy-relevant interactions inside the atmosphere and between the atmosphere and the ground are based on convection(67%), evaporation/condensation(22%), and radiation(11%) – dominated by convection, the interaction with empty space is restricted to radiation. From the previous arguments it is clear, that relevant radiation is restricted to the „top of atmosphere“. To be precise, it is the range with less than 1 optical depth „distance“ to empty space. This „distance scale“ depends strongly on the wavelength of the infrared light.

From the emission spectrum of Outgoing Longwave Radiation (OLR) we can infer essentially 3 cases:

• At wavenumbers of $800-1250 cm^{-1}$ there is the „atmospheric window“, where the (cloudless) atmosphere is nearly transparent to the infrared radiation – the optical depth spans the whole atmosphere, and the radiation temperature corresponds to the temperature of the earth’s surface of 280-310 K.
• Between wavenumber $600-750 cm^{-1}$ there is the $CO_2$-Band. $CO_2$ is homogeneously distributed in the atmosphere, with the radiation maximum in the stratosphere, corresponding to a rather low radiation temperature of about 220 K, a temperature amazingly stable w.r.t. both $CO_2$-concentration and surface temperature.
• Overlapping with the $CO_2$ band is the water vapor band from $300-1000 cm^{-1}$ . From Fig. 3 follows that there is a sharp decline of water vapor concentration at 5 km height. Therefore the radiation temperature of the water vapor band is considerably higher than that of $CO_2$ , appr. 250-280 K. Due to the fact that $CO_2$ reaches higher altitudes due to homogeneous distribution, water vapor emissions within the $CO_2$-Band are absorbed by higher reaching $CO_2$ molecules and are eventually emitted by $CO_2$ at a higher altitude and mostly lower temperature (over Antarctica the $CO_2$ emissions are at a higher temperature compared to the surface). This is the actual phenomenon that makes the greenhouse effect.

Lacking

• precise measurement data of these 3 emission components, measured locally at all latitudes,
• detailed knowlegde about cloud cover, which considerably changes the behaviour of the „atmospheric window“

we simplify the calculation by assuming an average „fixed“ radiation height $h$ of all 3 radiation components by demanding energy balance of averaged solar insolation and the validity of the Stefan-Boltzmann law at height h, with TOA incoming flux $S$, global average albedo $\alpha$ and the Stefan-Boltzmann constant $\sigma$ and the wellknown result for the effective temperature: $$ T_e = \sqrt[4]{\frac{S\cdot(1-\alpha)}{4\cdot \sigma} } = \sqrt[4]{\frac{1370 \cdot(1-0.3)}{4\cdot 5.67\cdot 10^{-8} } } K = 255 K $$

Is global averaging legitimate?

I am aware that there are doubts about globally averaging the flux due to the nonlinear relation between flux and temperature as well as strongly changing flux and albedo with latitude (see also here, p. 18). I had these doubts myself, but considering all the other errors we make with such a simplified model, under the realistic condition of relatively small day/night temperature deviations due to heat storage ( within $\pm 25 C$) the error of global averaging is small enough to be neglected (<1%), and the nonlinear SB equation can be expanded linearly around the global average flux $S_0$ and the global average temperature $T_0$: $$ \frac{\Delta T}{T_0} \approx \frac{1}{4}\cdot\frac{\Delta S}{S_0}$$ As a side effect this gives the simple relation between any radiative flux changes and expected temperature changes – important in the discussion about climate sensitivity -, that relative temperature changes are 25% of the relative flux changes.

Interpretation of the effective Temperature

The key point here is that this effective temperature is not a surface temperature, but it is located somewhere in the atmosphere, „averaging“ over the different levels of radiation of the contributing components. It is a fruitless undertaking to assume this to be a virtual surface temperature, leading to endless discussions about the underlying assumptions (what would be the „true“ albedo, is liquid water heat storage „allowed“, is there no atmosphere or an atmosphere without greenhouse gases, etc. ). And, most important, only under the assumption of such a fictive surface temperature, the definition of which is rather arbitrary, „forcing“ is required to „raise“ the temperature to the level of the actual surface temperature.

The expected altitude $h$ of the equilibrium temperature $T_e$ is easily computed from the assumed linear lapse rate (moist adiabatic lapse rate is not quite linear) and the actually measured average surface temperature $T_s$: $$h=\frac{T_s-T_e}{\Gamma}=\frac{287-255}{6.4} km = 5 km $$
It is important to note, that the lapse rate describes a state of an adiabatic thermodynamic equilibrium, i.e. the temperature difference between the surface and the the altitude $h$ does not imply any energy imbalance in need of „forcing“. Regarding radiative processes (which contribute by 11% of the interaction in the troposphere) this thermodynamic equilibrium means that inbound radiation is equal to outbound radiation at each location, with thermodynamics governing the process.
This equilibrium is, of course, only stable under the assumption of a constant in-flux at the surface or by direct atmospheric SW absorption which compensates the radiation losses at the top of atmosphere. Any changes such as day/night variation, seasonal or other weather variations obviously create energy fluxes, not to forget the permanent lateral flux due to latitudinal temperature gradients. The reactions to these are, however, always directed towards the entropy maximizing state of the optimal lapse rate.

In my understanding it is somehow misleading and the cause of misunderstandings to try to emulate the lapse rate equilibrium by means of virtual radiative fluxes. Nevertheless I do not deny the possibility to map the true thermodynamic behaviour into an „energy flux and budget“ model, with (among other energy fluxes) 2 more or less equal radiative fluxes of different signs (downwelling and upwelling IR), both larger than the actual SW flux from the sun, as it is commonly done. The important constraint on these models must be that the partition temperatures are determined by the given lapse rate, so that the thermodynamic fundament constrains radiation. Only then the radiative model is consistent with the thermodynamic model. Undeniable fact is that only the – positive – difference $\Delta F$ between upwelling and downwelling IR flux corresponds to an actual flow of heat: $$\Delta F=\epsilon\cdot (T_1^4 – T_2^4)$$

All those who consider this approach to be „heretic“, may be reminded that James Hansen used the same logic and equations in the introduction of his famous 1984 paper.

The implications of this understanding regarding the $CO_2$-sensitivity are discussed on the page „Physics of the the Greenhouse effect“ and regarding cloud and water vapor feedback on the page „Clouds and water vapor„.