Physics of the green house effect

[latexpage]

The current environmental policy of many countries seems to know only one goal, the avoidance of the „climate-damaging greenhouse gas“ $CO_2$. Its harmful effectiveness is questioned by „climate sceptics“ and „climate realists“. The public discussion gives the impression that this in reality difficult scientific question could be decided by polemics and insults and by majority building in political committees or the ballot box, with the flimsy and fundamentally false assertion that things are simple and completely clarified by science. Conversely, the complexity of the issue, the details of which are not completely overlooked by any single person, seduces ideologically biased groups to dominate the public debate towards their dubious political agenda with difficult-to-understand half-truths or even blunt lies.

For me as a physicist this situation is unacceptable. It is possible to clarify the question of the influence of the gas $CO_2$ on the earth’s temperature on the foundations of physics, which have grown for centuries and have become universally accepted knowledge.
As about 10 publications on the topic of climate change are currently published daily, the topic cannot be dealt with in all details here.   
But due to the approach to build exclusively on undisputed assumptions, I see this contribution as an opportunity to finally address and clarify the topic on a factual level.
Of course, this may include a hard discussion, which will then hopefully be conducted in the spirit of this contribution, as objectively as possible and on the basis of the undisputed prerequisites.  I expect that both „sides“ will „rub“ against these arguments. 

The argumentation presented here is not new, and to a certain degree it is not even controversial to IPCC publications. Some of the necessary physical findings have been known for over 100 years. The individual arguments have already been published by other authors. In my opinion, what is missing is an understandable, objective and 100% comprehensible chain of argumentation.
If I’m wrong, I like to be taught better with convincing arguments, but not with the infinitely stupid, unscientific argument that almost all scientists agree on certain statements.  That would be the end of all scientific progress.       

This contribution has the goal of

• drawing consistent conclusions from undisputed physical conditions,
• adequately presenting and critically discussing the central „greenhouse gas“ thesis,
• correctly interpreting recent measurements from satellites and other measuring equipment,
• letting qualified, truthful voices have their say. 

If you want to skip the following nontrivial physical theorems and the derived complex arguments, you can jump to the Summary. 

Basics of Atmospheric Physics

The following physical laws form the physical basis of the considerations about the influence of $CO_2$ on climate change. Implicitly further laws of nature come into effect (Planck’s radiation, Einstein coefficients, etc.)

Thermal state equation of ideal gas

The thermal state equation of ideal gases, often referred to as the ideal gas law, describes the relationship between the thermal state variables of an ideal gas: $$p\cdot V=n\cdot R\cdot T$$ with p: Pressure, V: Volume, n: Number of moles , T: Temperature and universal gas constant $R$: $$R= 8.314463\cdot \frac{m^3 \cdot kPa}{K\cdot mol}$$ With Mass m, Molar mass $M$ and $n=m/M$, as well as density $\rho$ and molar gas constant $R_m$ related to air $$\rho=\frac{m}{V} R_m=\frac{R}{M} = 287.05\frac{J} {K\cdot kg}$$ the thermal state equation becomes: $$p = R_m \cdot \rho\cdot T $$ Density multiplied by temperature is proportional to pressure, the proportionality constant depending only on the molar mass of the atmosphere.

Barometric
Elevation Formula and Adiabatic Temperature Gradient

An important undisputed basis of the following considerations is the dry adiabatic temperature gradient (technical term DALR). dry adiabatic lapse rate), implying that the temperature in the atmosphere decreases with altitude: $$\Gamma=\frac{dT}{dh} = – \frac{g}{c_p} = – \frac{9.81 \frac{m}{s^2}}{1.005 \frac{J}{gK}}} = -9.76 \frac{K}{km}$$ For the damp adiabatic temperature gradient (abbreviation MALR or SALR moist or saturated adiabatic lapse rate) are also valid adiabatic conditions, but explicitly in case of condensation of water vapour. The condensation heat (latent heat) of 2257 kJ/kg contained in the gaseous state of aggregation is thus released and increases the perceptible thermal energy of the air. The dry adiabatic temperature gradient is attenuated by this additional energy supply – without temperature change. This results in the extended barometric formula for pressure and density of the weather- and climate-determining troposphere (the lower 10-12km of the atmosphere) for the height-dependent pressure progression:$$p(h_1) = p(h_0)\cdot(1-\frac{\Gamma\cdot(h_1-h_0)} {T(h_0)})^{\frac{g}{\Gamma R_m}} $$ With the isentropic exponent $\kappa$, the ratio of the specific heat at constant pressure and at constant volume $$\kappa = \frac{c_P}{c_V} = 1.4$$ for dry air then applies to density: $$\rho(h_1) = \rho(h_0)\cdot(1-\frac{\Gamma\cdot(h_1-h_0)} {T(h_0)})^\frac{g}{\Gamma R_m {\Huge \kappa}} $$ These equations form the basis of the so-called „Standard atmosphere„, which has proven itself reliable in aviation for decades:

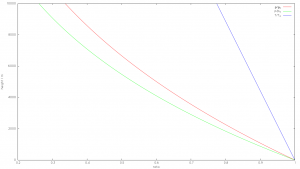
Fig 1: Standard atmosphere, temperature, pressure and density curves

The equations qualitatively indicate that

• temperature
• Pressure
• Density

strictly decrease with increasing height. With density and pressure, this is immediately apparent, as the atmosphere becomes thinner and thinner towards the outside until it merges into the vacuum of space. Regarding temperature it is less intuitive, but every mountaineer knows that the temperature decreases by about 1 degree per 100m altitude rise. In humid air it is less due to the condensation heat of the water, on a global average the temperature gradient can be assumed to be approximately -6.5 degrees/km, with fluctuations between -4 degrees/km and -9.6 degrees/km. The decisive point is that the temperature gradient (lapse rate) is completely determined by gravity in the form of standard acceleration and the specific heat capacity including latent heat for condensation.

However, this applies only at local thermodynamic equilibrium. Vividly, a local thermodynamic equilibrium means that you can measure temperature with a thermometer. The temperature decrease stops at the tropopause, because due to the low air density the condition of the thermodynamic equilibrium is no longer fulfilled and radiation effects predominate. However, the troposphere, which is defined by the existence of the temperature gradient, determines the climate.
Weather-related short-term and small-scale exceptions are also possible, for example in inversion weather conditions, the causes of which are well known to meteorologists. When there are such exceptions for whatever reason, there is still a strong forcing towards the described equilibrium state.

It is decisive for the barometric elevation formula, that the differences in temperature, density and pressure are derived solely from the two main laws of physics and the assumption of thermodynamic equilibrium, and apply to arbitrary gas accumulations in gravitational fields, without any reference to possible greenhouse gases or external energy sources such as the sun: If any gas accumulation is located in a gravitational field (at a constant gravitational field and sufficient pressure for the thermodynamic equilibrium of at least 0.1 bar) the distribution of pressure, density and temperature given by the adiabatic temperature gradient and the expanded barometric elevation formula.

This does not say anything about the absolute value of the temperature at the earth’s surface. This, of course, depends on the solar radiation and the factors to be discussed in the further course. The altitude-dependent atmospheric temperature changes in the thermodynamic equilibrium are, however, exclusively determined by the gravitational constant and the specific heat.Consequently all further conclusions apply to all planets of the solar system. Thus the conclusions can be and have indeed been examined.

Some climate research publications raise the suspicion that
their authors are of the opinion that greenhouse gases are
responsible for the course of temperature in the atmosphere. This
must be contradicted resolutely. There is no scientific reason
to postulate any cause for the temperature gradient other than
energy conservation (1st law of physics) and the assumption of
thermodynamic equilibrium. This is the state of maximum entropy in
the sense of the 2nd law of physics. For the climate-relevant
considerations it is sufficient to assume a local thermodynamic
equilibrium.

Radiation transport equation

A central role in the question of the influence of greenhouse
gases is played by so-called „radiative forcing“, the temperature
increase of the earth’s atmosphere and surface through absorption
of infrared radiation by greenhouse gases and re-emission of these
excited molecules. Therefore, it is necessary to take a closer look
at the interaction between radiation and greenhouse gases.

The absorption, scattering, and emission of electromagnetic
radiation in a medium is described by the radiative
transport equation.  This equation is highly complex and I
do not go into details here. The following undisputed properties of
the radiative transport equation are important for the following
reasoning:

The absorption of radiation increases with the density
of the medium. The emission of radiation increases with increasing
temperature of the medium.

The attenuation of the solar radiation hitting the earth and the earth’s atmosphere due to reflection is carried out by means of the so-called Albedo factor a (0..1). The fraction a of the radiation is reflected back into space,   (1-a) is the part of the active effective radiation. The measured albedo of the earth varies between 0.2 (=20% reflection) at the equator and 0.7 (=70% reflection) at the poles. The Earth’s mean albedo is about 0.3.
Fig. 2 shows the wavelength ranges in which the different air components absorb radiation.

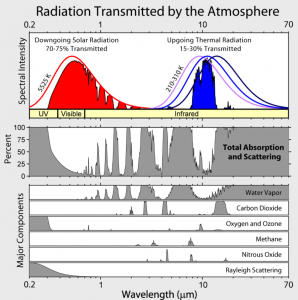
Abb 2: Absorption of air components

Stefan Boltzmann Law

The Stefan Boltzmann Law is a physical law that states the thermally radiated power of an ideal black body as a function of its temperature $$ P= \sigma \cdot A\cdot T^4 $$ with P: Radiant power, A: cross-sectional area, T: absolute temperature, $\sigma$ Stefan Boltzmann constant (definition and values of natural constants in Wikipedia Article): $$\sigma = \frac{2 \pi^5 k_B^4}{15 h^3 c^2}= 5.670374 \cdot 10^{-8} \frac{W} {m^2 K^4} $$ Simplifying assumption: It is usually assumed that both the sun and the earth behave like ideal black bodies. For more differentiated calculations, the Planck’s law of radiation is used. 
The area-related solar radiation at the edge of the Earth’s atmosphere is assumed to be constant and is called the solar constant S: $ S=1370\frac{W} {m^2}$

Theoretical surface temperature of the
earth

Assuming a stationary state, the radiation incident from the sun
is equal to the radiation emitted from the earth.
This results in a very simplified formal result as theoretical
surface temperature of the Earth:
$$T=\sqrt[4]{\frac{S\cdot(1-a)}{4\cdot\sigma}} = 255K$$ This
theoretical temperature is 33 degrees lower than the actual mean
temperature of 288K (=15 degrees Celsius). However, the model of a
black body without atmosphere on which this calculation is based is
inconsistent in two respects:

• The albedo originates to a large extent from the clouds, but clouds only exist in an atmosphere, as a consequence the „base temperature“ should be computed without cloud albedo, only surface albedo of $a=0.14$ should be used for the temperature computation, with a resulting equlibrium temperature T=268 K. The „atmospheric effect“ would be reduced to 20 degrees K.
• The irradiation of the earth’s surface is not homogeneous, as the model suggests, but strongly inhomogeneous. Not only do the poles receive much less radiation (none at all at polar night) than at the equator, the albedo is also much higher there. 

Therefore, a careful calculation must take into account the
static and dynamic effects of the atmosphere as well as the
irradiation dependent on the degree of latitude.
The latter topic  would, however, go beyond the scope of this
contribution and must be moved to a future article. 
Furthermore, the complex weather events and the important influence
of energy storage in the oceans and the influence of air and ocean
currents remain unconsidered for the time being. 

Explanation of the temperature discrepancy by
„radiative forcing“

There are countless sources of the „greenhouse“ effect, which also differ in details.
A core statement of the published „greenhouse“ effect is that part of the heat emitted from the Earth’s surface is transported back to the Earth’s surface by the greenhouse gases, especially $CO_2$, through radiation effects, i.e. absorption and emission. As representative references we refer to the two Wikipedia articles The ideal greenhouse model or The greenhouse effect where the following diagram comes from. This model is described here under the topic radiation budget:

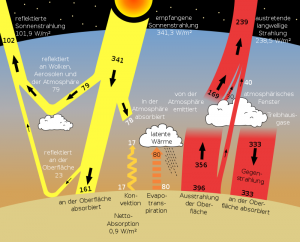
Abb 3: Standard radiation model of the IPCC with heat flows

Discussion of the
publicly represented IPCC „Greenhouse“-approach

The classic greenhouse is based on the fact that heat convection is prevented by the glass roof – when the glass roof is opened, the greenhouse effect disappears. There is no such „barrier“ in the atmosphere; convection ensures rapid compensation towards local thermodynamic equilibrium. The „real“ greenhouse effect also has nothing to do with the fact that the glass is not transparent to infrared. When using infrared transmissive panes, the greenhouse effect is almost as large as with normal panes. The naive notion of a greenhouse is therefore not applicable to the atmosphere.

The atmospheric „greenhouse“ theory is mainly based on radiation effects of $CO_2$, but its public presentation largely ignores the fact that up to 10 km altitude, i.e. in the troposphere, the energy exchange is dominated by thermodynamics, i.e. 67 % convection, 11 % radiation, and 22 % condensation of water vapour.

An essential element of the published „greenhouse“ approach is
that the existing $CO_2$ (and other greenhouse gases) will
„reflect“ heat back to the earth’s surface. There is talk of
„counter radiation“. However, this is not possible in an atmosphere
that is in local thermodynamic equilibrium with largely linear
temperature gradients – like our troposphere – for the following
reason:

It is true that $CO_2$ molecules are excited by the infrared radiation coming from the earth. The transfer of the absorbed energy can take place either by collisions with neighboring molecules (thermalization) or by emission. An excitation can also occur through an impact of a neighboring molecule. In the troposphere, the transfer of energy by impact is much more likely because the mean time to the next impact is much shorter than the mean residence time in the excited state. The radiation at emission is isotropic to all directions.

With respect to the question of whether it is possible for net radiation to occur „downwards“, it is crucial that the probability of radiation absorption and emission according to the radiative transport equation is proportional to the density (and temperature at emission) of the existing $CO_2$ molecules . But since both density and temperature decrease from bottom to top according to the barometric elevation formula with constant temperature gradient, net heat transfer from bottom to top takes place exclusively – under otherwise identical conditions. This is also in accordance with the second law of thermodynamics, according to which heat cannot be transferred from a colder body to a warmer one. The only locations where a downward radiation can take place, is within 1 optical depth above the surface. This overlaps, however, considerably with conduction and convection.

Typical dwell times (lifetimes) of the excited states and the
mean peak times at atmospheric pressure conditions as a function of
wavelength are shown in the following figure:

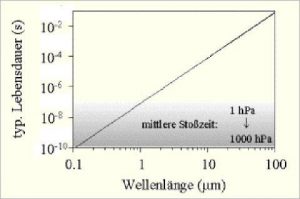
Abb 4: Excited states and peak times at $CO_2$

Air molecules collide under atmospheric pressure conditions after a time of $10^{-10}$ to $10^{-8}$ seconds. (Grey area). Greenhouse gases absorb IR radiation (in the range of 1 – 100 micrometers) and are excited. The lifetime of the excited state is depending on the wavelength between $10^{-7}$ and $10^{-1$} seconds, so it is significantly longer than the collision time. Spontaneous emission is therefore hardly satisfied, but air heating occurs due to collisions – with all types of gas. The radiation that arises at the – according to the probabilities small – share of spontaneous emissions is generated at the resonance frequency of the greenhouse gas and is therefore absorbed again within the immediate vicinity. This explanation is in contrast to the common narrative in climate science.

Explanation of the temperature discrepancy due to „adiabatic
greenhouse effect“

Obviously, the atmosphere causes the temperature difference of
about 33 degrees. 2 properties of the atmosphere discussed above
are the key to understanding:

1. The atmosphere is largely opaque to infrared radiation (Fig. 2). Only about 30% can be emitted unhindered. The rest is absorbed by the atmosphere, mainly via atmospheric „greenhouse gases“ such as water vapor, $CO_2$ and methane. The greenhouse gases are exchangeable. $CO_2$ has no special role compared to water vapor, which is 30 times more frequent, except that it absorbs radiation from a different, much narrower wavelength range. More importantly, the thermal energy is immediately distributed to other gases such as oxygen and nitrogen as a result of impact processes. The energy heats the air where it is absorbed and is gradually transferred to higher atmospheric layers by convection, radiation and evaporation/condensation with simultaneous adiabatic cooling.
   With increasing altitude and thinner atmosphere, the proportion of heat energy radiated into space increases because the absorbing gases become thinner. From the outside, the adiabatic greenhouse effect results from the fact that the radiation does not originate from the earth’s surface, but from a higher air layer at a usually (not always) lower temperature.
2. The temperature gradient in the atmosphere. Starting from the total mass of the atmosphere, the temperature-dependent barometric height formula provides a largely linearly falling temperature curve from the earth’s surface to the edge of the troposphere. This temperature curve is forced by the Boltzmann distribution of the energy of an atmosphere in the planetary gravitational field in the state of thermodynamic equilibrium.

With the extremely simplified consideration – for the sake of illustrative calculation – that no heat energy is radiated directly from the earth, i.e. that the infrared radiation absorption is complete up to a limit height, and from there stops abruptly, a fictitious height can be calculated from which the radiation is radiated into space – at the temperature present there. This height is frequency or wavelength dependent and is determined in such a way that up to the vacuum of space a optical thickness of 1 results.
With the usually assumed mean temperature gradient of -6.5 K/km, the temperature of the stationary equilibrium of 255K prevails at a height of about 5 km. Interestingly, this is the maximum level of water vapour in the atmosphere. A refined calculation would result in a different „effective emission height“, but would not change the qualitative result and would require at least a model including clouds. This simplified derivation is basically identical to the (extremely concise!) description of the model of James Hansen, who also explicitely makes use of the lapse rate.
Decisive for the „adiabatic greenhouse effect“ is the optically dense part of the total mass of the atmosphere (e.g. Hans Jelbring, The „Greenhouse Effect“ as a function of atmospheric mass, but restriction to „optically dense“ is not considered there), the „greenhouse gases“ play on the one hand the role of a wavelength-dependent „catalyst“ for the conversion of radiation energy into kinetic energy (temperature), on the other hand for radiation into space according to the emission spectra.

Interpretation of infrared emission spectra

Emission spectra of the atmosphere measured by satellites are available, these naturally depend on location and time of day. It must be said, that the displayed resolution of these spectra is much higher than what has actually been observed, that means the spectra are actually simulated and fitted by the measured data, which are in fact only 8 spectrometer measurements, 7 of which are within the $CO_2$-band.

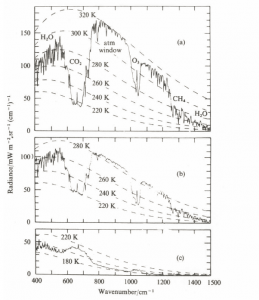
Abb 5: Measured radiations in the Sahara, Mediterranean and Antarctic, with the nimbus satellite (1971, from Bergmann-Schäfer, Textbook of Experimental Physics, Vol. 7, 1997)

For upward infrared radiation, this means that the radiation emitted from the ground is almost completely eliminated due to the strong absorption and is replaced by the inherent radiation of those colder atmospheric layers that are close enough to space not to be reabsorbed.
In the case of a spectrum recorded by satellites, the energy thus comes from different absorbers and wavelength from different altitudes in the atmosphere. The $CO_2$ absorbs the infrared radiation in the range of wavenumbers 600-750/cm. From the emission spectrum it follows that in this range the radiation does not take place as usual from a temperature range of 255-300 K, but only at 220 K. The infrared radiation is absorbed in the range of the wave numbers 600-750/cm. Due to the fact that the radiation into space is proportional to the 4th power of the radiation temperature, this means that less energy flows into space in the $CO_2$ range. This has the consequence that the whole atmosphere heats up a little more than if $CO_2$ were not present, and the energy would be distributed over all wavelength ranges. If the „normal“ radiation temperature is lower than 220 K, then the presence of $CO_2$ results in a negative greenhouse effect, in the $CO_2$ band and also in water vapor more energy is emitted than if the „greenhouse gases“ were not present, and the effect is a cooling.  This is not hypothetical,in the Antarctic the negative greenhouse effect is proven (Fig. 5, see also here). 
Therefore, the term „greenhouse gas“ is very misleading, because  whether $CO_2$ causes relative warming or cooling, or whether there is no $CO_2$ influence at all,   depends on various influencing factors. 

CO₂-Earth atmosphere
sensitivity

The crucial „greenhouse“ question is how the total temperature will change in this way when the $CO_2$ content of the atmosphere doubles from the pre-industrial 280 ppm to e.g. 560 ppm. This is called the $CO_2$ sensitivity. The current $CO_2$ value (2019) is about 415 ppm.
The interrelations are complicated, and in the public discussion the convictions are very different especially with this topic.
The „skeptics“ are of the opinion that

• that $CO_2$-sensitivity (global warming when the $CO_2$-content of the atmosphere is doubled) is below 1 degree,
• other influencing factors (plant growth, deserts, cloud formation) have an influence of similar magnitude or larger as $CO_2$,
• the feedback effects between $CO_2$, water vapor and oceans do not amplify each other, but rather attenuate each other

The goal here is to first get a comprehensible, consensusable statement about the pure $CO_2$ sensitivity. Surprisingly, this is in fact quite simple, and I wonder why this way was not published anymore.  However, the model used is static and very simple and does not take into account weather influences nor influences of the oceans.  But the radiation transport important for the significance of the $CO_2$ influence is well illustrated. And the target quantity „radiated energy“ allows subsequent averaging over the whole earth’s surface due to the additivity of the energy at the chosen points.

The key is the public program MODTRAN, which has been
used for many years for spectroscopic investigations, especially in
climate research.
With this program it is possible to model the absorption spectrum
of the atmosphere quite reliably, and thus it is possible to
calculate the radiation of the earth’s surface taking into account
the greenhouse gases and other conditions at one location at a
time. By selecting the standard atmosphere described above and the
average surface temperature of 288 K (= 15 degrees C), a simple
global model is obtained.

Here first the modeling of the atmospheric absorption spectrum
prior to industrialization, i.e. with a $CO_2$ portion of
280ppm:

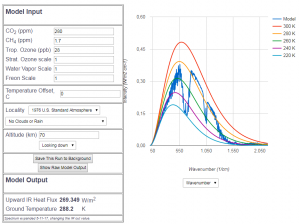
Abb 6: MODTRAN radiation model for
280 ppm $CO_2$ portion (year 1850)

between the wavenumber 550 and 770 is the clearly visible absorption by $CO_2$, which means a significant greenhouse effect compared to the complete absence of $CO_2$, the reduction of radiation due to the pre-industrial $CO_2$ is about 10% of the total radiation. But this is not a topic for discussion, because with less than 150ppm $CO_2$ content there is no life on earth. In the question of the „man-made“ greenhouse effect, 280 ppm is usually assumed to be the accepted reference. The truth of the matter is, that with 280 ppm the bulk of the „greenhouse“ effect has already happend, and further changes are minute.

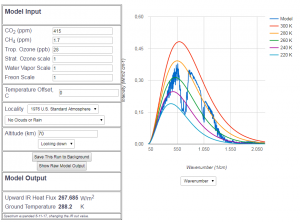
Abb 7: MODTRAN radiation model for 415 ppm $CO_2$ portion (year
2019)

Today’s spectral course of radiation, i.e. at 415 ppm $CO_2$, cannot be distinguished visually from the pre-industrial course at 280 ppm . The differences are a lot smaller than the measurment accuracy of satellites. This means in plain language that up to now nobody has ever proven the CO2-based greenhouse effect in a physically valid way. Only from model calculations, with many explicit and implicit assumptions, we have concluded a reduced heat flux by $1.66\frac{W}{m^2}$ compared to pre industrial times — provided nothing else except CO2 has changed in the atmosphere since 150 years ( 🙂 ). That would be $0.02\frac{W}{^2}$ per annum, which is about by a factor of 400 smaller than the measurement accuracy of satellites, which is $8\frac{W}{m^2}$ per annum .  Even the total hypothetical effect sind 1850 is below the measurement error by a factor of 5 (provided there had been a satellite in 1850). Analysing the energy budget at the earth surface also has a measurement error that is larger by an order of magnitude than the possible consequences of the green house effect.

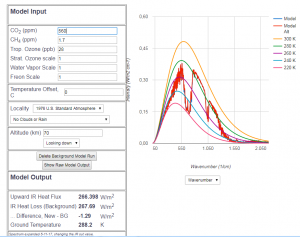
Abb 8: MODTRAN radiation model for 560 ppm $CO_2$ fraction (double
value of 1850), superimposed on the model with 415 ppm

In Fig. 8, the future hypothetical radiation pattern of 560 ppm $CO_2$ is directly superimposed onto the pattern of today. Again, the two curves are almost identical. The heat flow calculation results in a reduction of the radiated heat flow of about $1.3\frac{W}{m^2}$.  Although the difference of the $CO_2$ amount is larger than that of the past until today, the effect is smaller. This is due to the logarithmic dependence of the heat flow decrease on the $CO_2$ content. 

Doubling the $CO_2$ content $CO_2$ decreases the heat flux by $2.95\frac{W}{m^2} $, which corresponds to a hypothetical heating of the simple model atmosphere by a total of 1 degree. As can be easily validated with the interactive model program, this applies to every doubling of the $CO_2$ content. With increasing $CO_2$-content its greenhouse effect decreases . This important dependence – counteracting alarmism – is not disputed by any climate researcher, but strangely enough it is almost only publicly mentioned by „climate sceptics“. 

These very simple calculations are confirmed by an IPCC publication (TAR, 2001). On p. 357, the $CO_2$-related change in radiation since industrialization is given as $1.46\frac{W}{m^2}$, and $3.7\frac{W}{m^2}$ if doubled. (Which is strange because of the expected damping effect at higher $CO_2$ content )

Radiation and temperature
sensitivity

The immediate result of the MODTRAN simulation is radiation sensitivity, since the beginning of industrialization  until today $1.66\frac{W}{m^2}$ , which is more than the IPCC calculated value of $1.46\frac{W}{m^2}$ — whose value also takes into account the damping aerosols.  
Consequently, I use the MODTRAN simulation again to answer the issue of surface temperature sensitivity: By how much is the base temperature of the earth’s surface to be increased in order to obtain with increased $CO_2$ the same radiation as at the beginning of industrialization? For today’s value of 415 ppm, there is an increase of 0.4-0.6 degrees, depending on the interaction with water vapor. This is less than the common understanding of a temperature increase of 0.9-1 degrees since the beginning of industrialization.  The sensitivity to doubling is 0.75-1 degrees according to the MODTRAN model.
That raises the question, if there are not other factors besides $CO_2$ that can influence the temperature?  And why do the IPCC models come to clearly different results, although the IPCC results for the radiation are still almost the same as those determined here. If the sensitivity is simply calculated with the total derivative of the Stefan-Boltzmann law, even smaller values are obtained. These results indicate that the influence of $CO_2$ on climate change is a minor effect whose significance in the climate discussion is greatly exaggerated – so small that it is far below the measurement accuracy possible so far! This should make every reasonable person think  

It is my hope that this compilation of the physical fundamentals
represents a foundation that is capable of consensus in the best
sense of the word, from which the climate discussion will again be
conducted by all participants with objective arguments.

Open questions

It is quite clear that the above explanations do not yet include
a complete „climate model“. There is no doubt that many questions
remain unanswered which will be addressed in future
contributions:

• The influence of feedback between $CO_2$ content and water vapor or clouds, in the opinion of IPCC-related scientists, is the decisive aspect — if the feedback is positive.
• the influence of aerosols,
• the importance of the world’s oceans for the climate,
• the processing and evaluation of other possible climate-relevant influences such as solar cycles and magnetic solar activity,
• the importance of cosmic radiation,
• the climatic impact of the $CO_2$ additional greening of the earth,
• the consideration of the climate zones by regional models

Despite these limitations, there are significant consequences from these considerations:

Summary

Let me state first, that the low concentration of $CO_2$ is as such no reason for not having a big effect. In fact, the presence of this trace gas is a necessary precondition for all life on earth, which is a huge effect, and the first 150 ppm of $CO_2$ had a significant warming effect, as described above. However, the vast majority of today’s „greenhouse effect“, which warms the earth by an average of 33 degrees, is not caused by greenhouse gases, but by the thermodynamics of the total mass of the atmosphere: the thicker a blanket you cover yourself with, the better it retains the heat. The greenhouse gases water vapor and $CO_2$ have primarily the role of catalysts to convert radiation by absorption and molecular collisions into a warmed atmosphere and emit it again from sufficient proximity to space.
The specific contribution of the greenhouse effect by $CO_2$ can, depending on the environment, be positive (almost everywhere) or negative (at the south pole). The magnitude of the influence on changes of $CO_2$ is so small that the radiation spectra do not differ visually even if the $CO_2$ fraction is doubled. In addition, the sensitivity to $CO_2$ decreases with increasing $CO_2$ content — the change from 280 ppm to 415 ppm had about the same effect as the change from 415 ppm to 560 ppm. The effect of doubling without consideration of feedback factors is with $3\frac{W}{m^2}$ in the order of 1% of the total radiation and therefore to be regarded as minor. This results in a climate sensitivity of about 1 degree. The feedback effects will be discussed in detail separately, the simplification of ignoring them here is justified by observations that the climate models that include positive feedbacks, systematically overestimate the measured global temperatures of the last 20 years.

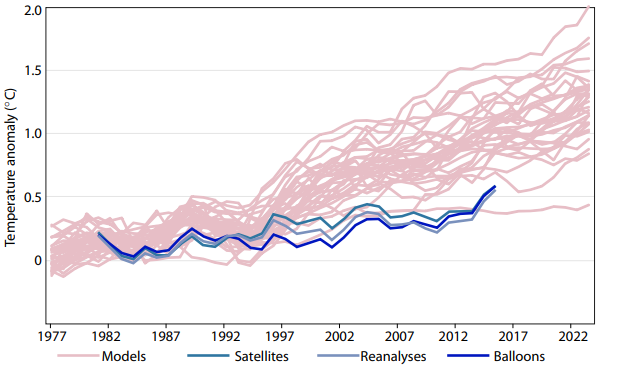
All models with feedback predict significant higher temperatures than were actually measured, whereas the simple model with only $CO_2$ forcing fits much better to the data between 1980 and now. This gives some confidence that there is no amplifying feedback effect, and that the temperature rise will not exceed 1.1 degrees C by the end of the century.