Der adiabatische Temperaturgradient – vereinfachte Herleitung

[latexpage]

Die atmosphärische Temperatur variiert mit der Höhe. Dieses wohlbekannte und gut verstandene Phänomen wird als Adiabatischer Temperaturgradient bezeichnet. Dieser beschreibt den Temperaturgradienten in der Höhe und besagt im Wesentlichen, dass die Temperatur pro km Höhe um 4-9,8 Grad Celsius abnimmt. Der Grund für die Erörterung dieses Phänomens ist, dass der vertikale Temperaturgradient oft fälschlicherweise einem strahlungsbedingten „Treibhauseffekt“ zugeschrieben wird, obwohl er in Wirklichkeit die natürliche thermodynamische Folge eines Gasvolumens in einem Gravitationsfeld ist. Da es sich um einen adiabatischen Effekt handelt, ist keine Änderung des Gesamtenergiegehalts beteiligt.
Es gibt viele Möglichkeiten, dieses Phänomen zu erklären. Hier möchte ich es auf die elementarste Weise tun.

Die erste wichtige Annahme ist das lokale thermodynamische Gleichgewicht. Das bedeutet, dass es in einem bestimmten Luftvolumen keine makroskopischen Zustandsänderungen z. B. bei Temperatur oder Druck gibt. Nehmen wir ein Luftvolumen an, das groß genug ist, damit die Temperatur definiert werden kann, und das klein genug ist, damit die Temperatur in diesem Volumen konstant ist, typischerweise „Gaspaket“ genannt.
Dieses Volumen mit der Masse $m$ befindet sich im planetarischen Gravitationsfeld mit der Gravitationskonstante $g$. In der Höhe h hat es die potentielle Energie $$ E_p = m\cdot g\cdot h. $$ und die thermische Energie dieses Volumens mit der Wärmekapazität (bei konstantem Druck) $c_p$ und der Temperatur $T$ gegenüber der Referenztemperatur $T_0$ ist
$$ E_t = c_p\cdot m\cdot (T – T_0) $$ Die zweite Annahme ist, dass das System adiabatisch ist, d.h. es fließt keine Energie in das System hinein oder aus ihm heraus. Das bedeutet, dass die Summe $E$ von $E_p$ und $E_t$ konstant ist:
$$ E = E_p + E_t = const. $$ Die Gesamtableitung von E muss also 0 sein: $$\frac{\partial E}{\partial h}dh + \frac{\partial E}{\partial T} dT = 0 $$ $$m\cdot g \cdot dh + c_p\cdot m\cdot dT = 0 $$ Daraus folgt direkt der Temperaturgradient:
$$ \frac{dT}{dh} = – \frac{g}{c_p} $$ Was bedeutet das? Ausgehend von der Annahme der lokalen Energieerhaltung verliert ein Molekül, das sich nach oben bewegt, Bewegungsenergie im Austausch gegen potentielle Energie, muss also um den entsprechenden Energiebetrag kühler werden, d.h. das Anheben einer Masse im Gravitationsfeld muss von der Bewegungsenergie bezahlt werden, und eine fallende Masse wird beschleunigt, wodurch die Temperatur steigt. Das Gleichgewicht ist erreicht, wenn die Entropie des Systems maximal ist.
Mit $g=9,81 \frac{m}{s^2}$ und $c_p = 1,012 \frac{J}{g\cdot °K} $ beträgt der adiabatische Temperaturgradient für trockene Luft $$ \Gamma = -\frac{9,81}{1,012} \frac{°K}{km} = -9.8 \frac{°K}{km} $$

Wenn die Luft feucht ist, kondensiert der Wasserdampf je nach Druck und Temperatur zu flüssigem Wasser, wobei die latente Wärme von 2260 J/g freigesetzt wird. Diese zusätzliche Kondensationsenergie verringert den Temperaturgradienten, da der „Preis“ für die potenzielle Energie (teilweise) aus der Kondensationsenergie bezahlt werden kann, ohne dass die Temperatur sinkt. Der resultierende feuchtadiabatische Temperaturgradient liegt im Bereich von -4…-9,8 °K/km, abhängig von der Luftfeuchtigkeit. Im globalen Durchschnitt beträgt der Temperaturgradient -6,4 °K/km.

Was hat der Temperaturgradient mit dem Klima oder dem Treibhauseffekt zu tun? Tatsächlich erklärt der Temperaturgradient einen Großteil, wenn nicht sogar den gesamten globalen Temperaturunterschied zwischen der Erdoberfläche und dem oberen Teil der Troposphäre, ohne dass explizite Annahmen über einen „Antrieb“ oder Treibhausgase gemacht werden (Treibhausgase sind jedoch für die Wechselwirkung mit der Infrarotstrahlung relevant). Der durch den Temperaturgradient beschriebene Zustand ist ein Gleichgewichtszustand der Atmosphäre ohne Energiefluss:

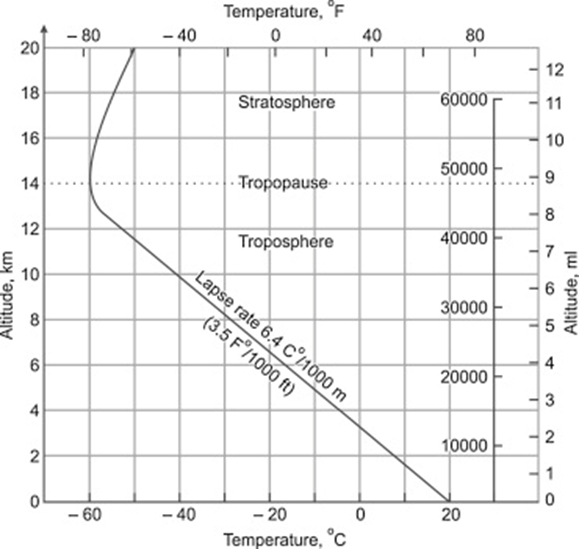
Wenn die Atmosphäre von diesem Zustand abweicht, zwingt die Thermodynamik das System stark in diese Richtung, so wie ein in einem Behälter verteiltes Gas zum Zustand gleicher Dichte tendiert. Die adiabatische Barometergleichung beschreibt den großräumigen Gleichgewichtszustand und stellt eine starke Korrelation zwischen dem Temperaturgefälle und dem Druckgefälle her. Daher wird manchmal der Begriff verwendet, dass „Druck die Temperatur verursacht“. Im Zusammenhang mit adiabatischen Bedingungen in einem Gravitationsfeld ist dies zwar nicht falsch, aber die Formulierung ist irreführend, so dass manche Leute fälschlicherweise glauben, dass statischer Druck Wärme erzeugen würde. Daher ziehe ich es vor, zur Beschreibung des Phänomens auf Grundprinzipien wie Energieerhaltung und Entropiemaximierung zu verweisen.

Das Konzept des adiabatischen Temperaturgradienten ist in der Atmosphärenforschung sehr mächtig: Im Jahr 1967 wurde die Oberflächentemperatur der Venus durch Auswertung des Temperaturgradienten korrekt bestimmt – ein expliziter Hinweis auf Treibhausgase war nicht erforderlich, obwohl implizit klar ist, dass die Infrarotstrahlung in den Weltraum von den Treibhausgasen aus der Nähe des Randes der Atmosphäre stammt. Unabhängig davon, wo das eintreffende Sonnenlicht absorbiert wird, verteilt sich die entstehende Wärme via Konvektion und Strahlung entsprechend des Temperaturgradienten.
Dies wurde kürzlich mit einer verbesserten Parametrisierung der Wärmekapazität neu berechnet.

Demzufolge handelt es sich bei der Venus keineswegs um einen „Runaway Treibhauseffekt“, die hohe Oberflächentemperatur hat ihre Ursache ich der sehr viel dickeren Atmosphäre als der der Erde, nur zu einem geringen Teil infolge der reinen CO$_2$-Atmosphäre.