Vorhersagen der globalen Temperatur

[latexpage]

Der traditionelle Ansatz wird in Frage gestellt

Die Schlüsselfrage zum Klimawandel ist Wie stark beeinflusst der $CO_2$-Gehalt der Atmosphäre die globale Durchschnittstemperatur? Und insbesondere, wie empfindlich reagiert die Temperatur auf Veränderungen der $CO_2$-Konzentration?
Wir untersuchen dies anhand von zwei Datensätzen, dem HadCRUT4-Datensatz zur globalen Durchschnittstemperatur und dem CMIP6-Datensatz zum $CO_2$-Gehalt.
Die Korrelation zwischen diesen Daten ist ziemlich hoch, so dass es ziemlich offensichtlich erscheint, dass ein steigender $CO_2$-Gehalt steigende Temperaturen verursacht.
Mit einem linearen Modell scheint es einfach herauszufinden, wie genau die Temperaturen im Jahr i $T_i$ durch den $CO_2$-Gehalt $C_i$ und das zufällige (Gauß’sche) Rauschen $\epsilon_i$ vorhergesagt werden. Aus theoretischen Überlegungen (Strahlungsantrieb) ist es wahrscheinlich, dass das Modell mit $log(C_i)$ am besten passt:
$T_i = a + b\cdot log(C_i) + \epsilon_i$
Die Konstanten a und b werden durch eine Anpassung mit der Methode der kleinsten Quadrate bestimmt (mit dem Python-Modul OLS aus dem Paket statsmodels.regression.linear_model):
a=-16,1, b=2,78
Daraus lässt sich die Sensitivität bestimmen, die als Temperaturdifferenz bei Verdopplung von $CO_2$ definiert ist:
$\Delta(T) = b\cdot log (2)$ °C = 1,93 °C
Das sind fast 2 °C, eine Zahl, die nahe an den offiziellen Schätzungen des IPCC liegt.

Was ist daran falsch, es scheint sehr einfach und logisch zu sein?
Wir haben das Residuum der Anpassung mit der Methode der kleinsten Quadrate noch nicht untersucht. Unser Modell besagt, dass das Residuum Gaußsches Rauschen sein muss, d.h. unkorreliert.
Der statistische Test, um dies zu messen, ist der Ljung-Box-Test. Betrachtet man das Q-Kriterium, so ist es Q = 184 mit p=0. Das bedeutet, dass der Residuum signifikante Korrelationen aufweist, es gibt strukturelle Informationen im Residuum, die mit dem vorgeschlagenen linearen Modell des log($CO_2$)-Gehalts nicht erfasst wurden. Ein Blick auf das Diagramm, das die angepasste Kurve zeigt, lässt erahnen, warum der statistische Test fehlgeschlagen ist:

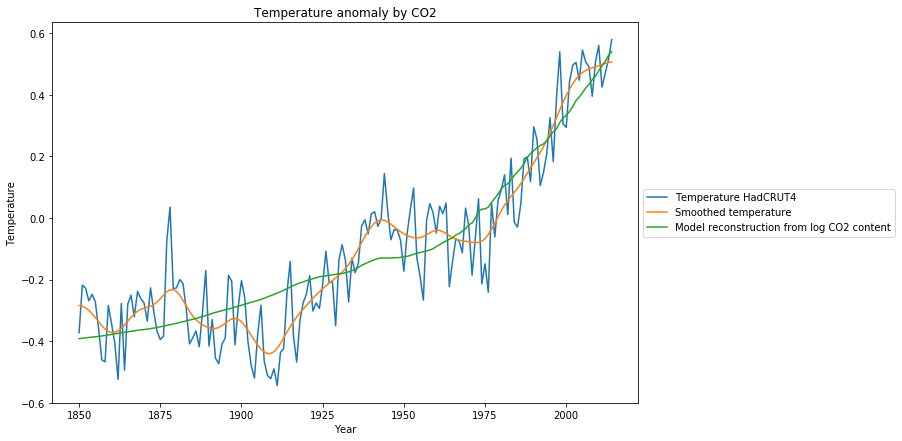
Wir sehen 3 Diagramme:

Die gemessenen Temperaturanomalien (blau),
die geglätteten Temperaturanomalien (orange),
die Rekonstruktion der Temperaturanomalien basierend auf dem Modell (grün)

Während das Modell im Vergleich zu den verrauschten Originaldaten vernünftig aussieht, ist es aus den geglätteten Daten offensichtlich, dass es neben $CO_2$ noch andere systematische Gründe für Temperaturänderungen geben muss, die vorübergehende Temperaturrückgänge wie während 1880-1910 oder 1950-1976 verursachen. Am überraschendsten ist, dass von 1977-2000 der Temperaturanstieg deutlich größer ist, als es das Modell des $CO_2$-Anstiegs erwarten ließe.

Die systematischen Modellabweichungen, u.a. ein 60-jähriges zyklisches Muster, sind auch zu beobachten, wenn man sich die Residuen der kleinsten Quadrate Schätzung anschaut:

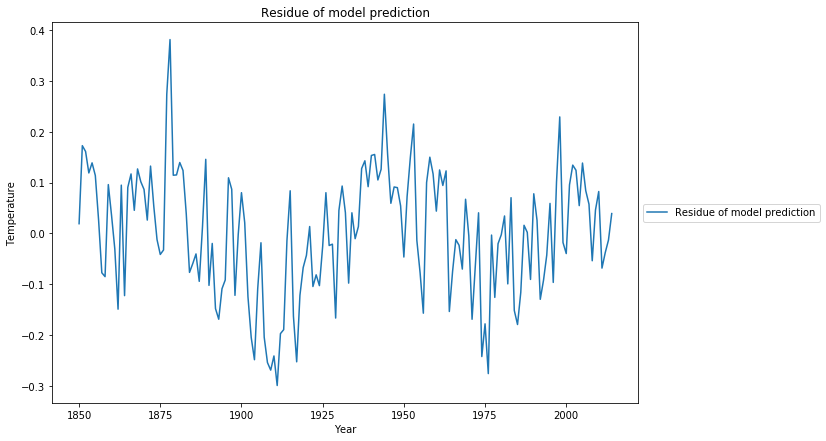
Erweiterung des Modells mit einer einfachen Annahme

Angesichts der Tatsache, dass die Ozeane und bis zu einem gewissen Grad auch die Biosphäre enorme Wärmespeicher sind, die Wärme aufnehmen und wieder abgeben können, erweitern wir das Temperaturmodell um einen Speicherterm der Vergangenheit. Ohne den genauen Mechanismus zu kennen, können wir auf diese Weise die „natürliche Variabilität“ in das Modell einbeziehen. Vereinfacht ausgedrückt entspricht dies der Annahme: Die Temperatur in diesem Jahr ist ähnlich wie die Temperatur des letzten Jahres. Mathematisch wird dies durch einen erweiterten autoregressiven Prozess ARX(n) modelliert, wobei angenommen wird, dass die Temperatur im Jahr i eine Summe von

einer linearen Funktion des Logarithmus des $CO_2$-Gehalts,log($C_i$), mit Offset a und Steigung b,
einer gewichteten Summe der Temperatur der Vorjahre,
zufälligem (Gauß’schem) Rauschen $\epsilon_i$

$ T_i = a + b\cdot log(C_i) + \sum_{k=1}^{n} c_k \cdot T_{i-k} +\epsilon_i $

Im einfachsten Fall ARX(1) erhalten wir

$ T_i = a + b\cdot log(C_i) + c_1\cdot T_{i-1} +\epsilon_i $

Mit den gegebenen Daten werden die Parameter geschätzt, wiederum mit dem Python-Modul OLS aus dem Paket statsmodels.regression.linear_model:
$a=-7.33, b=1.27, c_1=0.56 $
Die Rekonstruktion des Trainingsdatensatzes ist deutlich näher an den Originaldaten:

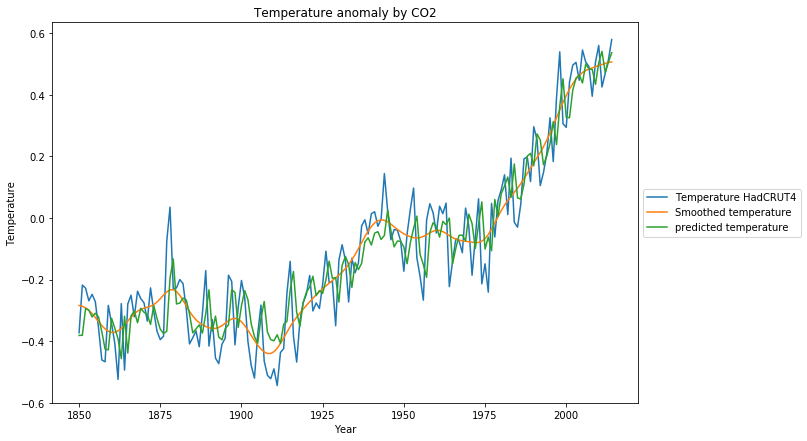
Das Residuum der Modellanpassung sieht nun viel mehr wie ein Zufallsprozess aus, was durch den Ljung-Box-Test mit Q=20,0 und p=0,22 bestätigt wird

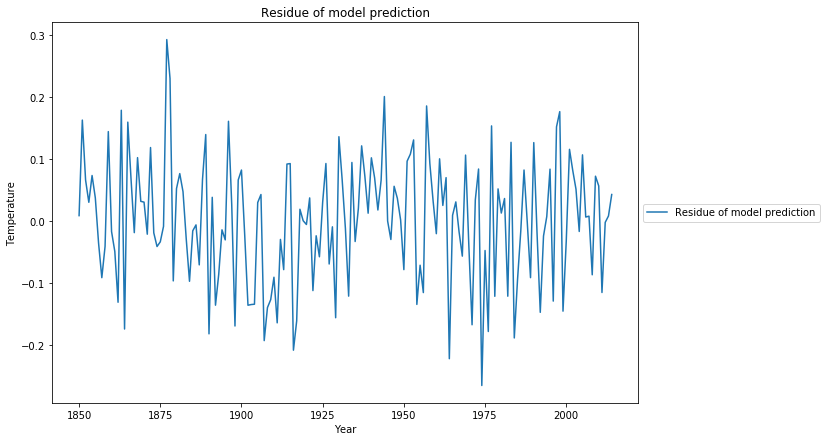
Bei Berücksichtigung der natürlichen Variabilität reduziert sich die Empfindlichkeit gegenüber $CO_2$ auf
$\Delta(T) = b\cdot log (2) °C = 0,88 °C $

In einem anderen Beitrag haben wir die Abhängigkeit des atmosphärischen $CO_2$-Gehalts von den anthropogenen $CO_2$-Emissionen untersucht, und dies als Modell für Vorhersagen des zukünftigen atmosphärischen $CO_2$-Gehalts verwendet. Es werden u.a. 3 Szenarien untersucht:

„Business as usual“ neu definiert anhand der neuesten Emissionsdaten als Einfrieren der globalen $CO_2$-Emissionen auf das Niveau von 2019 (was auch tatsächlich geschieht)
100% weltweite Dekarbonisierung bis 2050
50% weltweite Dekarbonisierung bis 2100
50% weltweite Dekarbonisierung bis 2050
sofortige 50% weltweite Dekarbonisierung (hypothetisch)

Das resultierende atmosphärische $CO_2$ wurde wie folgt berechnet, die statistischen Fehler sind so klein, dass die Prognose für die nächsten 200 Jahre sehr enge Fehlerintervalle aufweist.

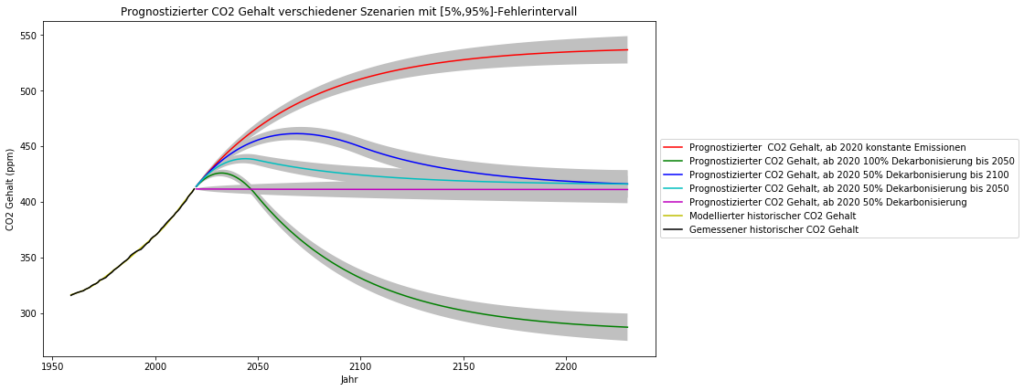
Füttert man das Temperatur-ARX(1)-Modell mit diesen vorhergesagten Zeitreihen des $CO_2$-Gehalts, so sind für die Zukunft folgende globale Temperaturentwicklungen zu erwarten:

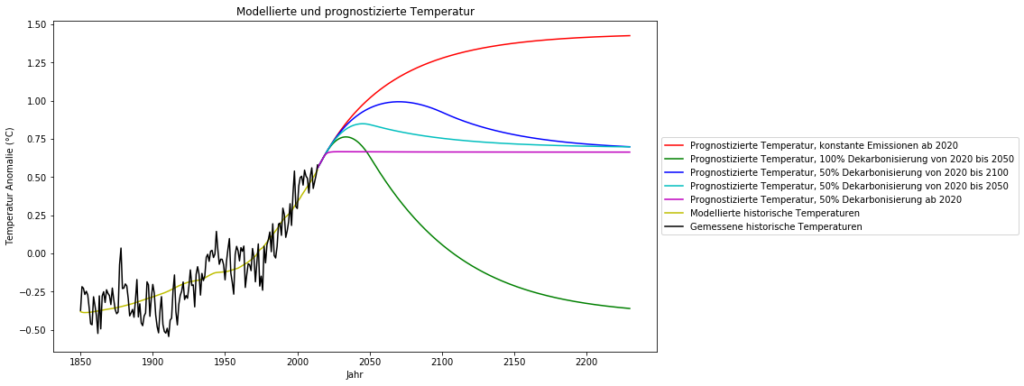
Schlussfolgerungen

Die folgenden Schlussfolgerungen werden unter der Annahme gezogen, dass es tatsächlich eine starke Abhängigkeit der globalen Temperatur vom atmosphärischen $CO_2$-Gehalt gibt. Ich bin mir bewusst, dass dies umstritten ist, und ich selbst habe an anderer Stelle argumentiert, dass die $CO_2$-Sensitivität bei nur 0,5°C liegt und dass der Einfluss der Wolkenalbedo viel größer ist als der von $CO_2$. Dennoch lohnt es sich, die Mainstream-Annahmen ernst zu nehmen und einen Blick auf das Ergebnis zu werfen.

Unter dem„business as usual“-Szenario, d.h. konstante $CO_2$-Emissionen auf dem Niveau von 2019, ist bis 2150 mit einem weiteren Temperaturanstieg um ca. 0,5°C zu rechnen. Das sind 1,4°C über dem vorindustriellen Niveau und damit unter der 1,5° C-Marke des Pariser Klimaabkommens.
Viel wahrscheinlicher und realistischer ist das Szenario „50%ige Dekarbonisierung bis 2100“ mit einem weiteren Anstieg um 0,25°C, gefolgt von einem Rückgang auf das heutige Temperaturniveau.

Die politisch propagierte „100%ige Dekarbonisierung bis 2050“, die nicht nur ohne wirtschaftlichen Zusammenbruch der meisten Industrieländer völlig undurchführbar ist, bringt uns zurück auf das kalte vorindustrielle Temperaturniveau, was nicht wünschenswert ist.