Cloud and Water climate feedback
[latexpage]
One key question in the climate discussion is whether the atmospheric water vapor and the clouds provide a net positive or negative feedback: When the atmosphere gets warmer, will the „water content“ magnify this or reduce it?
The issue is extremely complex, with the result that science is very divided about this, there are publications favoring positive and others favoring negative feedback.
In order to have a chance of logical reasoning, I will try to reduce the problem to its core by eliminating as much as possible of the dynamics.
The first point to make is that there are two kinds of feedback:
- The first feedback is the direct interaction between $CO_2$, water vapor, and clouds w.r.t. IR radiative behaviour as well as the SW relevant albedo. This will be the main focus of this contribution.
- Usually only a secondary water vapor and cloud feedback is considered, based on an assumed temperature rise by $CO_2$ alone. The very strong negative feedback of (mainly tropical) storms is hardly ever discussed. All these are very complex and are not handled here. For the time being I refer to the work of Prof. Richard Lindzen.
The approach uses the basic atmospheric radiative model as implemented in the MODTRAN software, which is well known and widely accepted.
3 model cases are investigated:
- Energetic equilibrium for an atmosphere without greenhouse gases
- Energetic equilibrium and $CO_2$ climate sensitivity for an atmosphere without water vapor but all other greenhouse gases
- Energetic equilibrium and $CO_2$ climate sensitivity for an atmosphere with water vapor and greenhouse gases, calibrated for the current albedo.
Atmosphere without greenhouse gases:
When there are no greenhouse gases, this implies that there is no water vapor in the atmosphere and therefore there are no clouds. From the earth’s energy budget (Fig 1) it follows that the average albedo a would be
$a=\frac{23}{23+161} =0.125$ instead of the current atmospheric value of appr. 0.3.
This thought experiment requires the „ceteris paribus“ assumption, i.e. everything else is assumed to be the same as in our real world climate system.
I explicity discard the discussion about „freezing oceans“ or about the question, how it is possible to have no water vapor when oceans are in fact creating it, because for the following considerations only the radiative behaviour of the atmosphere is relevant.
Lower average Albedo 0.125 instead of 0.3 implies: With this albedo the solar insolation and therefore the energy flux equiblibrium would be at
$340\frac{W}{m^2}\cdot (1-0.125) = 297.5 \frac{W}{m^2}$ instead of $240\frac{W}{m^2}$ as with $a=0.3$
and an average equilibrium temperature of 271 K = -2 C:
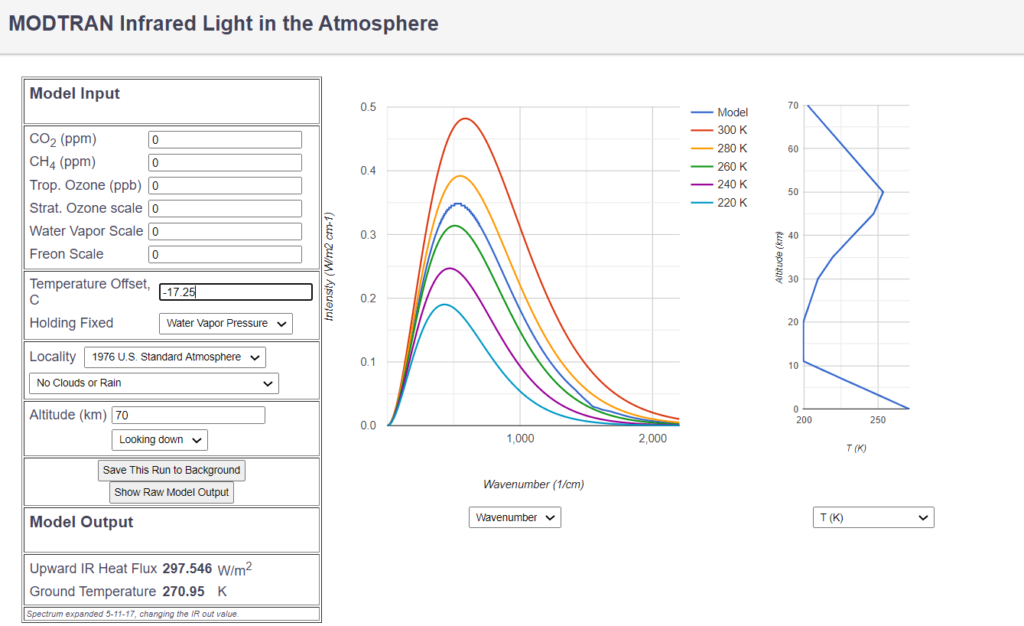
Therefore the answer to the question “What is the net warming effect from the
atmosphere, including all its processes, without changing anything else?” is 17 K and not 33 K as is usually communicated. The usual model assumption of constant albedo under the condition of „no greenhouse gases“ or even „no atmosphere“ is deeply flawed and misleading, because it implicitely makes cloud albedo to a constant without any justification. The contrary is the case – the change of cloud albedo turns out to be the dominant contribution to the atmospheric warming of the last 40 years.
Atmosphere with no water vapor, only CO2 and other GHG
This case investigates an atmosphere with no water vapor, containing only CO2 and other GHG.
Again there are no clouds nor water vapor, leading again to the lower average albedo $a=0.125$ instead of 0.3. With this albedo the energy flux equiblibrium would be at $297.5 \frac{W}{m^2}$ (instead of 240 as with $a=0.3$) and an average equilibrium temperature of 279.5 K = 6.5 C:
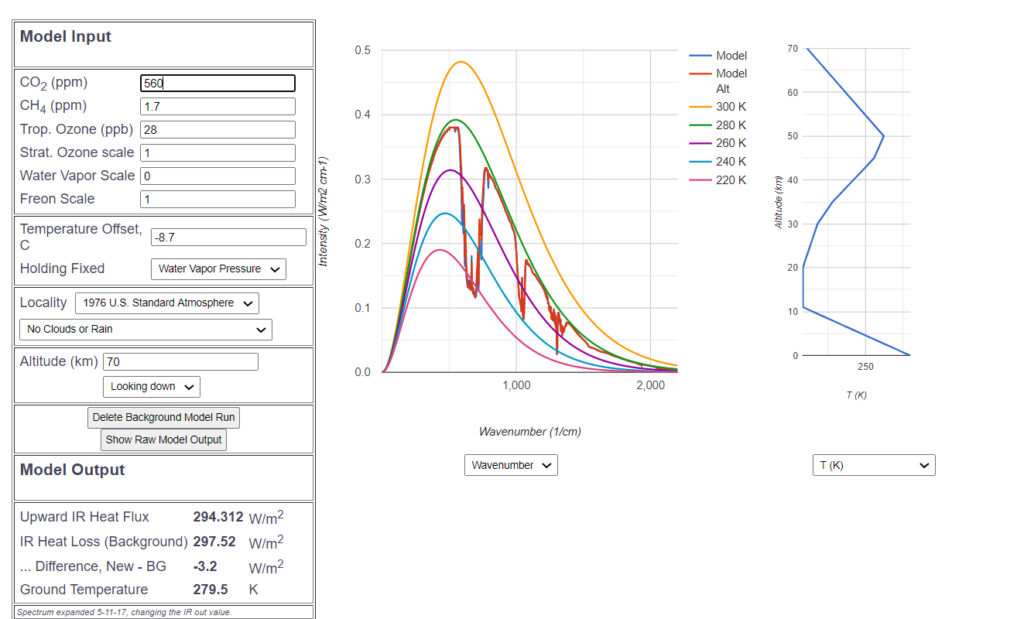
CO2-Sensitivity of doubling from 280ppm to 560ppm according to MODTRAN in atmosphere without water vapor would be $3.2 \frac{W}{m^2}$, resulting in a temperature sensitivity of 0.75 C. This is determined by adjusting the Temperature Offset in MODTRAN, until the „Difference New-BG“ becomes 0:
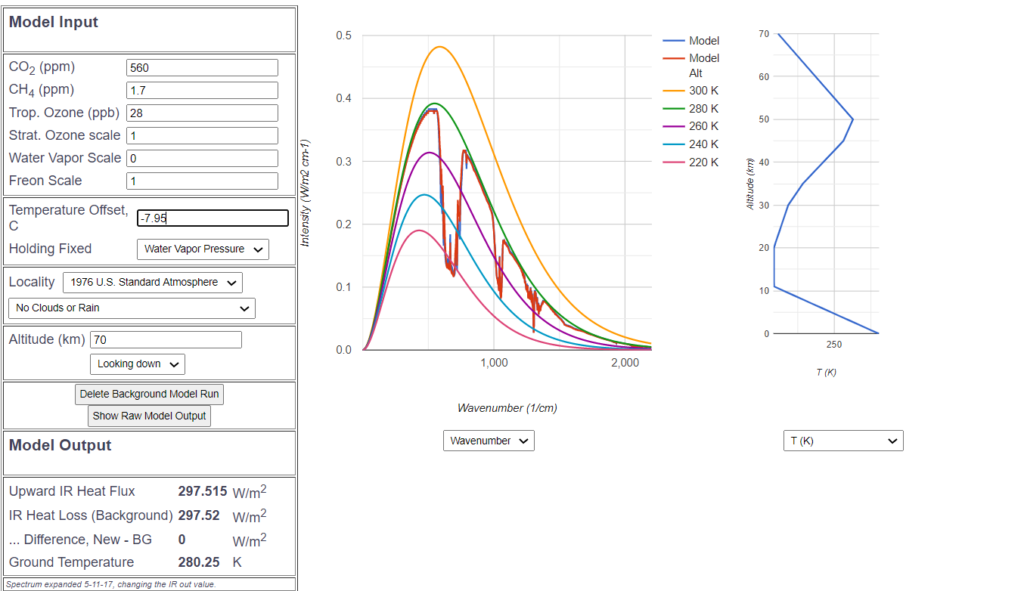
Including cloud model and water vapor
This investigation cannot provide a perfect cloud model. The only purpose is to come to a qualitative conclusion, whether clouds and water vapor feedback increases or reduces $CO_2$ sensitivity. The „reality constraint“ is that the cloud model should achieve the average equilibrium IR flux of $240 \frac{W}{m^2}$.
With the „Cumulus Cloud“, and a water vapor scale of 0.25 this can be achieved. The only other cloud model to achieve this is „Altostratus Cloud“ and a water vapor scale of 0.2. With both configurations the $CO_2$ sensitivity of doubling $CO_2$ from 280ppm to 560 ppm is $1.92 \frac{W}{m^2}$, considerably less than without water vapor content.
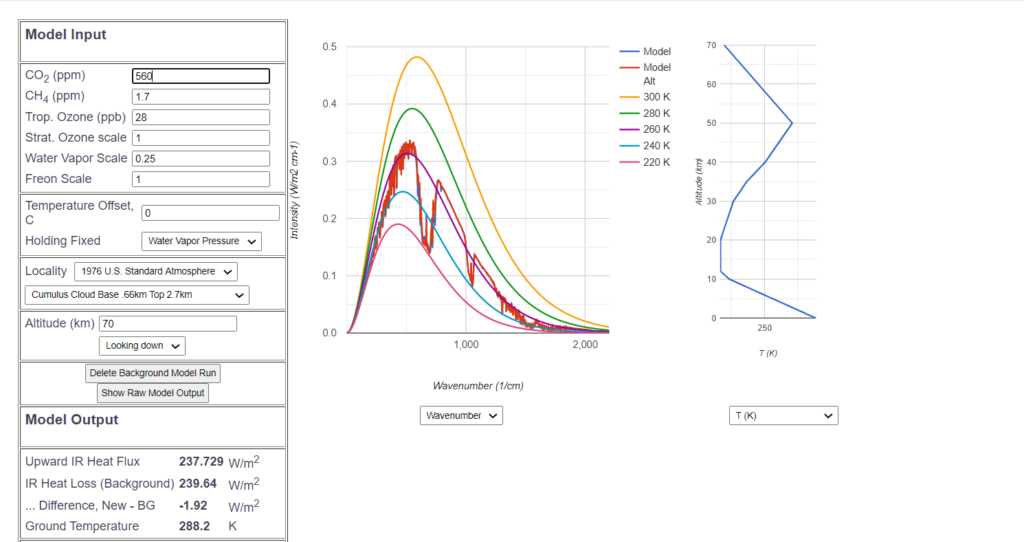
The temperature sensitivity of doubling $CO_2$ from 280ppm to 560 ppm in this case, which is the closest model to the real world, is reduced to 0.52 C:
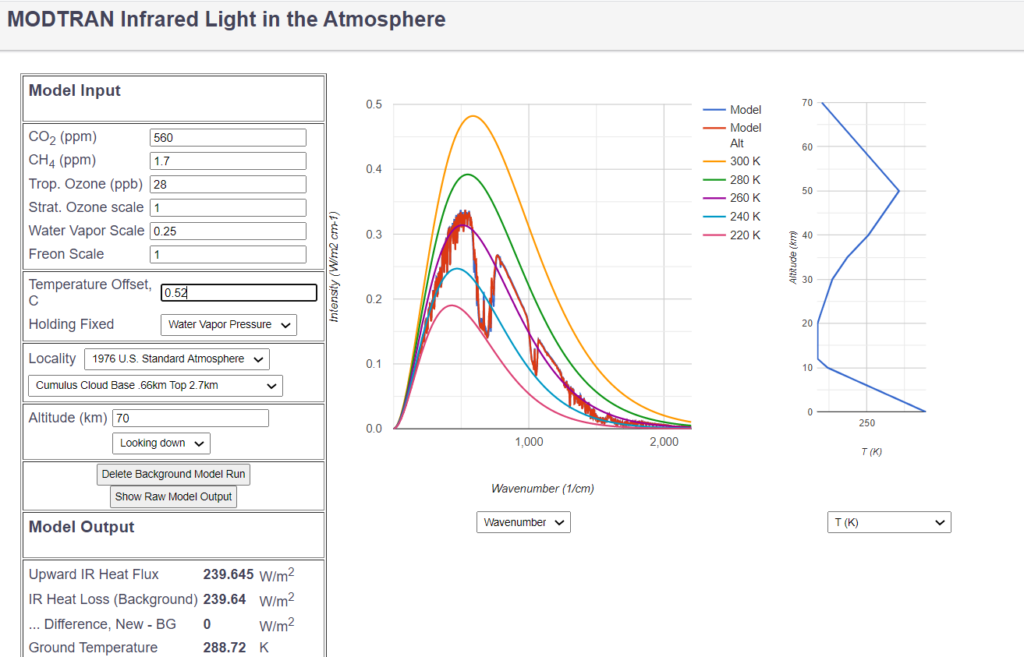
The change of $CO_2$-concentration between pre-industrial times (280 ppm) and now (415 ppm) therefore corresponds to an increase of average global temperature of 0.29 C.
This investigation has shown, that $CO_2$ sensitivity in the presence of water vapor and clouds is consistently smaller than without water content in the atmosphere. The consequence of this is that water vapor and clouds together reduce rather than enhance the greenhouse effect of $CO_2$, and total feedback of water vapor and clouds is negative, based on the MODTRAN radiative model.
The sensitivity of 0.52 C is so small that there is no reason to worry about future increases of $CO_2$ content in the atmosphere.